拱坝地基综合变形模量计算的有限元方法

，， ，立君

(1.三峡大学 水利与环境学院，湖北 宜昌 443002;

2.三峡水力发电厂，湖北 宜昌 443133;

3.漳河工程管理局，湖北 荆门 448156)

1 研究背景

到目前为止, 拱梁分载法[1]仍是拱坝结构分析的主要方法。但在采用拱梁分载法进行拱坝应力分析时，需要合理确定各计算高程坝基岩体的变形模量和泊松比[2]。而拱坝大多建在多种岩石组成的岩基上，坝基的综合变形参数不仅与各单层岩体的变形参数有关，还与各岩性岩体的厚度比例、岩层倾角有关，用其中任何一种岩性岩体的变形参数来代替或者对所有岩体变形参数进行简单的平均都是不合理的。因而合理正确地给出坝基的综合变形参数，对准确分析计算坝体应力具有十分重要的现实意义。

为此，周涛[3]提出采用平面有限元方法，按变位相等原理，分别得出各高程的拱向和梁向变形模量，将计算结果进行拱梁综合，从而得到各计算高程的地基的综合变形模量。但在综合过程中，权系数的选取往往依靠经验选取。

在材料科学领域，复合材料的等效性能研究是一个重要问题，已开展了相当多的研究工作，方法和模型也很多[4]，如自洽模型，Mori-Tanaka模型，Voigt-Reuss上下限模型，Eshelby模型，微分模型，Hashin-Shtrikma上下限模型等，这些方法中，有的预测的上下限范围很大，有的对弱化材料的形状有严格的要求，很难应用到坝基综合变形模量的计算中去。

事实上，宏观等效弹性特性是非均匀介质固有的物理特性之一，给定非均匀介质的细观结构及组分相的物理特性后，其宏观等效弹性性能就确定了，与其应力应变状态无关[5]。基于此，本文提出了利用三维线弹性有限元计算拱坝坝基综合变形模量和泊松比的一种数值计算方法，该方法考虑了等效弹性张量的各分量之间具有的耦合关系，并将求解结果与相关的理论解进行了比较。结果表明，利用该方法来计算等效综合变形模量和泊松比是可行的。可用于求解由多种不同岩性的岩体、断层以及软弱夹层等构成的复杂坝基的综合变形模量和泊松比，最后用该方法计算了锦屏一级拱坝坝基各高程的综合变形模量和泊松比。

图1 地基分区示意图

2 综合变形参数的有限元计算原理

为了计算拱坝第i层高程的某岸的综合变形参数，则在该高程单位高度范围内作用单位法向面荷载，采用如图1所示的地基分区。

地基参数取2种：一种为真实的非均匀、不连续的地基参数，由三维有限元求得该高程高度范围内在单位法向荷载作用下各点的变位(usi,vsi,wsi)；另一种为均匀各向同性地基参数(E0,μ0)，也可由三维有限元求得在单位法向荷载作用下该高程高度范围内各点的变位(u0i,v0i,w0i)。

由弹性理论知道，对于均匀各向同性地基，各点的变位与弹性模量之间呈线性关系，与泊松比呈非线性关系。因此，当均匀地基综合变形参数为(E,μ)时，则其近似的变位(uri,vri,wri)可按式(1)求得。其中ui,j，vi,j，wi,j，(j=1，2，3)分别表示关于μ的一阶、二阶和三阶偏导，μ=μ0+Δμ。

(1)

设非均匀不连续的真实地基与均匀地基(E,μ)所求得的变位之差的平方和为

(2)

按拱坝地基综合变形参数(E,μ)确定的位移场(ur,vr,wr)在最小二乘意义上逼近实际位移场(us,vs,ws)，实际上也就是求得综合变形参数E和Δμ，使得F(E,Δμ)=min，即令∂F(E,Δμ)/∂E=0,∂F(E,Δμ)/∂Δμ=0两式成立。

由此可得：

(3)

(4)

将式(3)和式(4)展开后可得式(5)和式(6)：

(5)

(6)

其中：

联立上述式(5)、式(6)2个非线性方程组，可求得E和Δμ，此即为计算高程处地基等效的综合变形模量E和泊松比μ。

3 数值算例

为了验证上述方法的正确性，下面对一个由2种材料组成的半无限空间弹性体的综合变形模量进行计算，并将求解结果与理论解进行了对比。设有理想的弹性半空间体，由2种材料组成，其材料参数分别为E1=10 GPa，μ1=0.25；E2=20 GPa，μ=0.2，两者体积各占一半，在计算范围内施加法向荷载。根据等效介质理论及本文方法求得其等效变形模量见表1。

表1 等效理论与有限元计算的变形模量对比

由表1可以看出，Voigt-Ruess模型得出的上下限非常粗糙，Eshebly模型、自洽模型、微分模型、Mori-Tanaka模型和Hashin-Shtriklllna模型预测的岩体等效弹性模量均在Voigt-Ruess模型上下限范围之内。并且Hashin-Shtrimkna模型上下限范围较小，除了Mori-Tanaka模型预测的结果不在Hashin-Shrtimkna模型上下限范围内，其余均在此范围内，说明了Eshelby模型、自洽模型、微分模型和Mori-Tanaka模型预测结果基本保持一致，Hashin-Shrtimkna模型上能给出最窄的上下限范围。

同时也可以看出，利用本文方法求出的综合变形模量在Hashin-Shtrikman模型上下限范围内，说明用来求解地基综合变形模量是可行的。

4 工程应用

4.1 工程概况

锦屏一级水电站位于四川省盐源县和木里县交界的雅砻江干流上，是雅砻江水能资源最富集的中下游河段五级水电开发的第一级。枢纽工程以发电为主，兼有防洪、拦沙等作用。拱坝坝顶高程1 885 m，建基面最低高程为1 580 m，最大坝高305 m，坝顶厚度13 m，拱冠梁最大底厚58 m。水库正常蓄水位1 880 m。坝址处于深山峡谷，岸坡陡峻，物理地质现象发育，岩体变质程度深浅不一，构造复杂，主要地质构造有断层、深部裂缝、层间挤压带及变形拉裂岩体等。

4.2 有限元模型

4.2.1 计算范围

计算范围以坝轴线为中心，向上游1倍坝高，下游2倍坝高，沿顶拱坝肩向两岸各1.5倍坝高，建基面以下1倍坝高，顶拱向上取40 m，整个计算范围约1 400 m×1 000 m×700 m。计算模型充分考虑了河谷地形主要特征，模拟了右拱端上游的普斯罗沟，坝肩槽开挖坡模拟了左岸存在的f5,f8断层、煌斑岩脉和右岸的f13,f14,f18等地质结构；模拟了坝区分布的各种岩体岩级；模拟了基础处理措施。

4.2.2 有限元模型

计算中采用空间8结点等参元，用线弹性有限元进行模拟，共有118 845个结点，119 256个单元。有限元模型见图2。

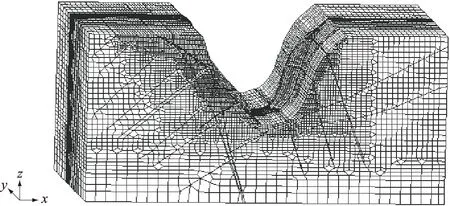
图2 三维有限元计算网格

在计算过程中，左右岸、上下游及底面各个边界均为法向约束。其中x方向为垂直于河流方向，从左岸指向右岸为正；y方向为顺河流方向，指向下游为正；z方向为铅直向上为正。

4.3 材料参数

在三维有限元计算中共有11种材料，具体材料力学参数见表2。

表2 材料力学参数

4.4 计算结果

计算了天然情况下各高程地基综合变形模量，以及按照设计加固方案加固后的各高程地基综合变形模量和泊松比，计算结果见表3。在充分考虑各种地质构造和地基处理措施后，采用该方法计算的地基综合变形模量是合理的[6]。

表3 锦屏地基综合变形模量

5 结 论

本文借助于三维有限元法，为拱坝坝基综合变形参数的计算提供了一种行之有效的数值计算方法。该方法要求按综合变形参数确定的位移场在最小二乘意义下逼近于实际结构中的位移场，从而也考虑了综合变形模量和泊松比等参数之间的关系。计算过程中模拟了实际地形、岩性分区和节理构造等诸多因素，反映实际地形地质条件对综合变形模量的影响，解决了拱梁分载法进行坝体应力分析时很难给出比较合理的综合变形参数的问题。计算结果表明：本文的方法可靠，计算结果合理，可以广泛应用于拱坝坝基综合变形参数的计算。

参考文献：

[1] 朱伯芳,高季章,陈祖煜，等.拱坝设计与研究[M].北京:中国水利水电出版社,2002. (ZHU Bo-fang, GAO Ji-zhang, CHEN Zu-yu,etal. Design and Research for Concrete Arch Dams[M]. Beijing: China Water Power Press, 2002. (in Chinese))

[2] 林绍忠,苏海东.复杂岩基上的拱坝多拱多梁法应力分析[J].长江科学院院报,2002,19(5):27-30. (LIN Shao-zhong, SU Hai-dong. Stress Analysis for Arch Dams on Complicated Rock Foundation Using Trial Load Method[J]. Journal of Yangtze River Scientific Research Institute, 2002,19(5):27-30. (in Chinese))

[3] 周 涛.溪洛渡水电站拱坝基础综合变模分析[J].四川水力发电,2001,20(2): 89-93. (ZHOU Tao. Study on Overall Deformation Modulus for Arch Dam Foundation at Xiluodu Hydropower Station[J]. Sichuan Water Power, 2001,20(2): 89-93.(in Chinese))

[4] 杜善义,王 彪.复合材料细观力学[M].北京:科学出版社,1998. (DU Shan-yi, WANG Biao. Composite Micromechanics[M]. Beijing: Science Press, 1998. (in Chinese))

[5] 陈作荣,诸德超,陆 萌.复合材料的等效弹性性能[J].复合材料学报, 2000, 17(3):73-77. (CHEN Zuo-rong, ZHU De-chao, LU Meng. Effective Elastic Properties of Composites[J]. Acta Materiae Compositae Sinica, 2000, 17(3):73-77. (in Chinese))

[6] 彭 辉,刘德富,陈和春.锦屏拱坝基础变形模量多目标非线性规划研究[J].中国农村水利水电,2005,(11),62-65. (PENG Hui, LIU De-fu, CHEN He-chun. Study on the Multi-objective Non-linear Programming of Foundation Deformation Modulus of Jinping Arch Dam[J]. China Rural Water and Hydropower, 2005,(11): 62-65. (in Chinese))