基于Copula函数的鄱阳湖都昌站枯水多变量频率分析
,,
(武汉大学 水资源与水电工程科学国家重点实验室,武汉 430072)
1 研究背景
枯水是天然的河流、湖泊每年都会发生的季节性现象,是水文过程中不可或缺的重要组成部分。但由于早期枯水对人类的影响较小,其研究水平远不及洪水。随着社会经济的发展,水资源供需矛盾日益突出,尤其在枯水季节,由于河流径流量减少,加之人类过度开发利用枯水资源带来了水质污染加重、河流断流、地面沉降等一系列问题,人们越发重视枯水问题[1]。对于干旱缺水地区,枯水的主要基本特征,更是供水工程规划设计、水资源优化配置和合理保护的重要依据[2]。
目前,大部分的枯水研究集中于河流枯水径流的研究[1-6]。但对于处在有明显干、湿季节的地区的天然湖泊,由于降雨的季节性差异,直接影响了地表和地下径流的形成,因而湖泊与之对应分为丰水期和枯水期,其水文特征迥异[7],因而很有必要对其枯水特征开展研究。湖泊枯水的研究成果较为有限,如梁明川[7]对天然湖泊进行枯水期水文分析, 建立水均衡方程,然后利用水文、气象资料计算流域地下水资源。谭国良等[8]针对近年来鄱阳湖频繁出现的干旱现象,采用长系列枯水期资料分析了鄱阳湖区枯水特征及其成因。现有工作均未全面揭示湖泊枯水特征变量的概率统计特征。
枯水并不等同于干旱,连续的季节性枯水事件并不一定会形成干旱,但由于它们在发生成因和演变规律上存在一定的联系且相互影响,因而在研究方法上可以相互借鉴。本文基于干旱分析中广泛采用的游程理论识别湖泊枯水,提取湖泊枯水特征变量,然后采用Copula函数进行湖泊枯水特征变量的多变量频率分析,为鄱阳湖区枯水季节的水资源管理提供理论参考。
2 研究区域与方法
鄱阳湖纳赣、抚、信、饶、修等5大河及湖区区间来水,经湖盆调蓄后由湖口注入长江。流域水网比较密集,鄱阳湖同时受到长江干流和五河的影响,由于江、湖、河枯期时间基本重叠,在一定程度上延长了湖区枯水持续时间,加剧了枯水程度,对于水资源管理极为不利[8]。近年来,鄱阳湖流域正面临着严重的干旱问题,给鄱阳湖流域和长江中下游地区造成了重大的经济损失。因此,正确认识鄱阳湖湖区枯水规律,是指导抗旱、保护生态、开发利用水资源和保证流域社会经济协调发展的重要准备工作。
本文选取都昌水文站作为鄱阳湖区代表水文站。都昌站地处鄱阳湖水域中间,其水位能较准确地代表鄱阳湖的水位数据,能反映出鄱阳湖的整体水情[9]。本文采用的数据为都昌水文站1958—2007年长系列日平均水位资料,数据来自江西省水文局。
2.1 枯水识别与枯水特征变量提取
一般而言,枯水期的起讫时间和历时,主要取决于水体的补给状况的确定,但实际操作上存在一定困难。本文采用在干旱分析中广泛采用的游程理论[10],进行湖泊枯水的识别,并提取枯水特征变量。游程理论一个重要前提是阈值的选取,本文作者认为,在一个完整的水文年内(枯水分析常用每年7月至次年6月[9]),当湖区代表站点日平均水位低于事先确定的阈值时,湖泊即进入枯水期。阈值可根据水位数据的分位数来确定,本文采用文献[9]中建议的鄱阳湖都昌站枯水划分标准,即都昌水文站水位12.8 m作为鄱阳湖进入枯水期的水位阈值。枯水事件的游程分析图如图1所示。

图1 湖泊枯水事件游程图
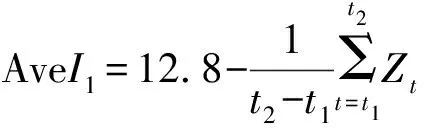
在基于日资料进行枯水统计的过程中,可能出现水位短暂地低于阈值,而后迅速恢复至阈值以上且量级较小的枯水过程,使得统计变得复杂,如图1(b)区中箭头所示。综合参考陆桂华等[11],Madsen和Rosbjerg[12]提出的方法,若某一段枯水过程的最大枯水强度小于造成明显取用水困难的临界强度(本文取1.0 m,对应水位11.8 m[9]),历时小于0.1E(D)时,该枯水过程忽略不计,E(D)指枯水历时的期望。

此外,当2个不能忽略的枯水过程中间还掺杂着若干可以忽略的枯水过程,如图1(d)区所示,此时枯水历时D4=t8-t7,相应得到平均枯水强度。
2.2 基于Copula函数的枯水多变量联合分布
2.2.1 Copula函数的性质
一个完整的水文事件往往包含多个特征变量,且特征变量之间通常存在相关性,Copula理论正是通过构造联合分布来描述这种相关结构的[14]。Copula是定义域为[0,1]均匀分布的多维联合分布函数,它可以将多个随机变量的边缘分布连接起来得到它们的联合分布。
Sklar定理:令H为一个n-维分布函数,其边缘分布为F1,F2,…,Fn,则存在一个n-Copula函数C,使得对任意x∈Rn [15],即
H(x1,x2,…,xn)=
Cθ(F1(x1),F2(x2),…,Fn(xn)) 。
(1)
式中θ为Copula函数的参数。
2.2.2 Archimedean Copula函数
Archimedean Copula函数结构简单,计算简便,可以构造出多种形式多样、适应性强的多变量联合分布函数,在水文分析计算中得到了广泛的应用[14,16-18],根据构造方式的不同可以分为对称型和非对称型2种。
基于前述方法识别枯水事件,分别提取枯水历时D、平均枯水强度AveI和最大枯水强度MaxI作为湖泊枯水特征变量,分别确定其边缘分布函数,然后通过三维非对称型Copula函数构造其联合分布。本文选用在水文领域较为常用的3种Archimedean Copula函数,即Gumbel-Hougaard,Clayton,Frank Copula函数,3种Copula函数的三维非对称形式如下。
Gumbel-Hougaard Copula函数:
C(u1,u2,u3)=exp{-[((-lnu1)θ2+
(-lnu2)θ2)θ1/θ2+(-lnu3)θ1]1/θ1},
1≤θ1≤θ2。
(2)
Clayton Copula函数:
C(u1,u2,u3)=
[(u1-θ2+u2-θ2-1)θ1/θ2+u3-θ1-1]-1/θ1,
1≤θ1≤θ2。
(3)
Frank Copula函数:
C(u1,u2,u3)=
(4)
式中:u1,u2,u3分别代表边缘分布函数;参数θ1和θ2通过极大似然法进行估计。
2.2.3 Copula函数的选择
拟合优度评价指标是选择分布线型的一个重要标准[14]。采用离差平方和最小准则(OLS)来评价不同Copula函数的拟合效果,选择最合适的Copula函数,其表达式为
(5)
式中:n为样本容量;Pei,Pi分别为经验频率和理论频率。
2.3 枯水事件的重现期分析
在水文分析中,确定某一稀遇事件或特大灾害发生的概率,具有十分重要的现实意义。工程中常用重现期来度量风险的大小。
枯水事件的单变量重现期为:
(6)
式中:TD,TAvel,TMaxI分别为枯水历时、平均枯水强度、最大枯水强度的单变量重现期;FD(d),FAvel(avei),FMaxI(maxi)分别为枯水历时、平均枯水强度、最大枯水强度的边缘分布函数。
一场完整的枯水事件包括枯水历时、平均枯水强度、最大枯水强度等多个变量,仅考虑某一个的重现期很可能高估或低估枯水事件出现的风险,因而必须分析多个枯水变量之间的相关性及其出现的联合重现期。
(7)
在给定变量Xk≤xk的前提下,事件Xi≤xi,Xj≤xj出现的条件概率为
(8)
对应的条件重现期的表达式为
(9)
3 结果与分析
3.1 边缘分布的建立
首先对提取的枯水特征变量进行“三性”检验,各变量均符合独立同分布假设。采用指数分布、Gamma分布、P-III分布、Weibull分布、Logistic分布和广义极值(GEV)分布分别拟合枯水历时、平均枯水强度和最大枯水强度,采用线性矩法估计分布函数的参数,对分布拟合效果进行K-S检验,并以前述离差平方和(OLS)公式(5)最小为准则比较确定最适宜拟合各变量的线型。
经计算,选用Weibull分布拟合干旱历时,Logistic分布拟合平均枯水强度,GEV分布拟合最大枯水程度。经验频率和理论分布的拟合结果如图2所示。拟合效果均通过了95%置信水平的K-S检验。从图2中可以看出,各种理论分布的拟合效果均较理想。

图2 理论边缘分布拟合
3.2 相关性分析
分别采用Pearson相关系数和Kendall秩相关系数计算3个变量的两两相关性,结果如表1所示。表中对角线上方元素为Kendall秩相关系数,下方元素为Pearson相关系数。从表中可知,各变量之间呈现明显的正相关性,平均枯水强度和最大枯水强度之间的相关性最高,枯水历时和最大枯水强度次之,枯水历时和平均枯水强度最弱。
3.3 联合分布的建立
应用极大似然法分别估计3种Copula函数的参数,构建3个变量联合分布,并计算各自理论频率与经验频率的离差平方和,相关结果如表2所示。

表1 枯水变量Pearson和Kendall秩相关系数

表2 Copula函数参数估计及OLS
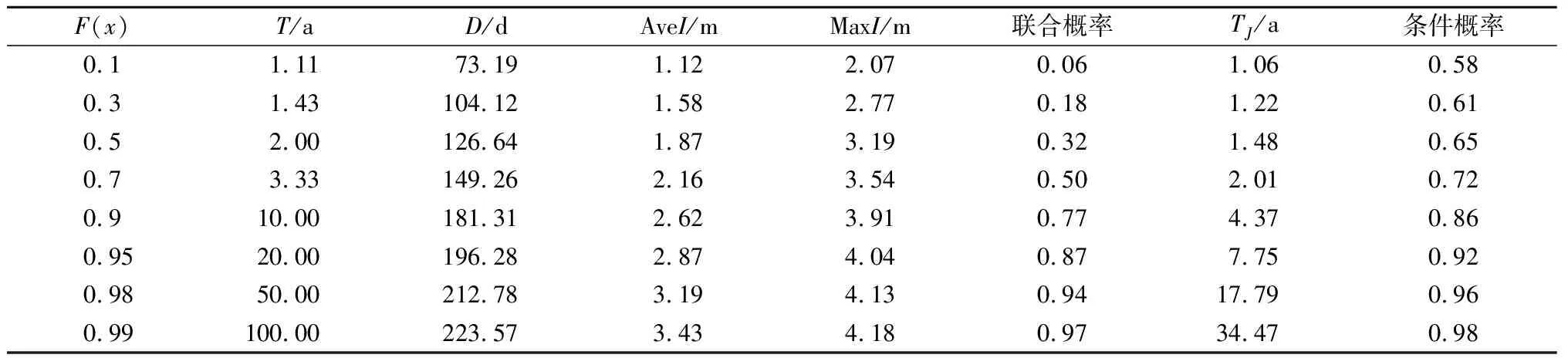
表3 联合概率(重现期)和条件概率结果统计
从表2中可以看出Clayton Copula的拟合效果优于其他2个连接函数,其OLS为0.034 7。

图3 理论分布与经验点据拟合
根据Genest和Rivest[19]提出的一种比较直观地评价Copula 函数的方法,分别计算理论概率估计值Kc(t)和经验频率估计值Ke(t),然后点绘Kc(t)和Ke(t)关系图,如果两者相关系数较高且图上的点均匀地落在45°线附近,那么表明Kc(t)和Ke(t) Copula函数拟合得较好。点绘Clayton Copula函数计算得到的理论分布与经验频率关系图如图3所示。从图3可以看出,理论和经验分布的相关系数为0.990 3,且点据均匀地落在45°线附近,可知构造的Copula函数是合理的。
3.4 枯水概率和重现期分析

根据建立的联合分布,可以推求枯水事件的联合重现期和给定其中一个变量时的条件重现期。单变量的重现期T由边缘分布确定。根据联合概率,由式(7)计算联合重现期TJ,结果均列于表3。由表3可知:3个变量的联合重现期随着单变量的重现期增加而增加,单变量的重现期要高于3个变量的联合重现期。以边缘分布函数F(x)等于0.99时为例,此时单变量重现期为100 a,而联合重现期为34.47 a,二者差异明显。
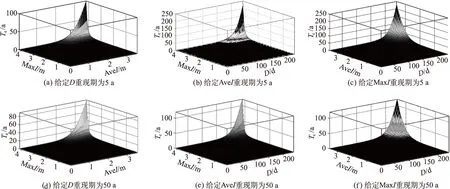
图4 枯水事件的条件重现期
采用式(9),计算分别给定枯水历时、平均枯水强度和最大枯水强度的单变量重现期为5 a和50 a时,事件E={Xi>xiorXj>xj|Xk≤xk}的条件重现期,结果如图4所示。由图4可知:给定枯水历时的单变量重现期时计算得到的条件重现期低于给定另外2个变量时的条件重现期。在给定枯水事件任一单变量的重现期时,计算得到的条件重现期随着另2个变量的单变量重现期的增大而增大。随着给定的单变量重现期的增大,另2个变量量级相同时的枯水事件条件重现期逐渐减小。
以上结果均表明构造的联合分布能提供更多的湖泊枯水信息,能更全面地反映枯水事件变量间的相关性特征。
4 结 语
研究湖泊枯水规律,对于湖泊枯水季节的管理具有重要意义。本文借鉴干旱分析中应用广泛的游程理论识别湖泊枯水,从鄱阳湖湖区都昌水文站长系列日平均水位资料中提取枯水历时、平均枯水强度和最大枯水强度作为湖泊枯水特征变量,确定其边缘分布函数,采用Archimedean Copula函数构造了变量的联合分布,依据离差平方和最小准则选用最优的Copula函数,分析枯水事件出现的概率,计算了枯水事件的联合重现期和条件重现期,结果表明:
(1) 建议选择Weibull分布、Logistic分布和GEV分布,分别作为边缘分布函数拟合鄱阳湖都昌站干旱历时、平均枯水强度和最大枯水程度。
(2) 依据离差平方和最小准则优选的Clayton Copula函数,适于用来拟合鄱阳湖都昌站枯水多变量联合分布。
(3) 联合分布考虑了枯水事件的多个变量,能提供更多的湖泊枯水特征信息,更能全面揭示湖泊枯水的概率统计特征。
参考文献:
[1] 殷福才, 王在高, 梁 虹. 枯水研究进展[J]. 水科学进展, 2004, 15(2): 249-254. (YIN Fu-cai, WANG Zai-gao, LIANG Hong. Advances in Low Flow Research [J]. Advances in Water Science, 2004, 15(2): 249-254. (in Chinese))
[2] 冯国章, 王双银. 河流枯水流量特征研究[J]. 自然资源学报, 1995, 10(2): 127-135. (FENG Guo-zhang, WANG Shuang-yin. A Study of the Characteristics of the Low Flows of Rivers [J]. Journal of Nature Resources, 1995, 10(2): 127-135. (in Chinese))
[3] SMAKHTIN V U. Low Flow Hydrology: A Review [J]. Journal of Hydrology, 2001, 240(3): 147-186.
[4] GOTTSCHALK L, YU K, LEBLOIS E,etal. Statistics of Low Flow: Theoretical Derivation of the Distribution of Minimum Streamflow Series [J]. Journal of Hydrology, 2013, 481: 204-219.
[5] 周 芬, 郭生练, 熊立华, 等. 枯水频率分析线型的比较研究[J]. 水文, 2006, 26(1): 28-33. (ZHOU Fen, GUO Sheng-lian, XIONG Li-hua,etal. Comparative Study on Distribution Functions for Low Flow [J]. Journal of China Hydrology, 2006, 26(1): 28-33. (in Chinese))
[6] 方 彬, 郭生练, 肖 义, 等. 基于低定量取样的枯水频率分析[J]. 武汉大学学报 (工学版),2006,39(2):1-4. (FANG Bin, GUO Sheng-lian, XIAO Yi,etal. Low Flow Frequency Analysis Based on LUT Sampling [J]. Engineering Journal of Wuhan University,2006,39(2):1-4. (in Chinese))
[7] 梁明川. 天然湖泊枯水期水文分析及流域地下水资源计算[J]. 水文地质工程地质, 1984, (4): 58-59. (LIANG Ming-chuan. Hydrology Analysis and Groundwater Resource Calculation of Nature Lake during Dry Season[J]. Hydrogeology & Engineering Geology, 1984, (4): 58-59. (in Chinese))
[8] 谭国良, 郭生练, 王 俊, 等. 鄱阳湖生态经济区水文水资源演变规律研究[M]. 北京: 中国水利水电出版社, 2013. (TAN Guo-liang, GUO Sheng-lian, WANG Jun,etal. Hydrology and Water Resource Variation Law of Poyang Lake Basin [M]. Beijing: China Water Power Press, 2013. (in Chinese))
[9] 闵 骞, 占腊生. 1952—2011年鄱阳湖枯水变化分析[J]. 湖泊科学, 2012, (5): 675-678. (MIN Qian, ZHAN La-sheng. Characteristics of Low-water Level Changes in Lake Poyang during 1952-2011 [J]. Journal of Lake Sciences, 2012, (5): 675-678. (in Chinese))
[10] YEVJEVICH V. An Objective Approach to Definitions and Investigations of Continental Hydrologic Droughts [M]. Fort Collins: Colorado State University, 1967.
[11] 陆桂华, 闫桂霞, 吴志勇, 等. 基于copula函数的区域干旱分析方法[J]. 水科学进展,2010,21(2):188-193. (LU Gui-hua, YAN Gui-xia, WU Zhi-yong,etal. Regional Drought Analysis Approach Based on Copula Function [J]. Advances in Water Science,2010,21(2): 188-193. (in Chinese))
[12] MADSEN H, ROSBJERG D. On the Modeling of Extreme Droughts [J]. IAHS Publications-Series of Proceedings and Reports-Intern Assoc Hydrological Sciences, 1995, 231: 377-386.
[13] TALLAKSEN L M, MADSEN H, CLAUSEN B. On the Definition and Modeling of Streamflow Drought Duration and Deficit Volume [J]. Hydrological Sciences Journal, 1997, 42(1): 15-33.
[14] 郭生练, 闫宝伟, 肖 义, 等. Copula 函数在多变量水文分析计算中的应用及研究进展[J]. 水文, 2008, 28(3): 1-7. (GUO Sheng-lian, YAN Bao-wei, XIAO Yi,etal. Multivariate Hydrological Analysis and Estimation [J]. Journal of China Hydrology,2008,28(3):1-7. (in Chinese))
[15] NELSEN R B. An Introduction to Copulas [M]. USA: Springer, 2006.
[16] 闫宝伟, 郭生练, 肖 义, 等. 基于两变量联合分布的干旱特征分析[J]. 干旱区研究,2007,24(4):537-542. (YAN Bao-wei, GUO Sheng-lian, XIAO Yi,etal. Analysis on Drought Characteristics Based on Bivariate Joint Distribution [J]. Arid Zone Research, 2007, 24(4): 537-542. (in Chinese))
[17] 闫宝伟, 郭生练, 肖 义. 南水北调中线水源区与受水区降水丰枯遭遇研究[J]. 水利学报, 2007,38(10):1178-1185. (YAN Bao-wei, GUO Sheng-lian, XIAO Yi,etal. Synchronous-asynchronous Encounter Probability of Rich-poor Precipitation between Water Source Area and Water Receiving Areas in the Middle Route of South-to-North Water Transfer Project [J]. Journal of Hydraulic Engineering, 2007,38(10):1178-1185. (in Chinese))
[18] CHEN L, SINGH V P, GUO S,etal. Drought Analysis Using Copulas [J]. Journal of Hydrologic Engineering, 2013, 18: 797-808.
[19] GENEST C, RIVEST L P. Statistical Inference Procedures for Bivariate Archimedean Copulas [J]. Journal of the American Statistical Association, 1993, 88(423): 1034-1043.
——江西省九江市都昌老年大学校歌

