基于格序理论的水利工程方案优选

魏光辉

(新疆农业大学 水利与土木工程学院，乌鲁木齐 830052)

基于格序理论的水利工程方案优选

魏光辉

(新疆农业大学 水利与土木工程学院，乌鲁木齐 830052)

针对水利工程方案综合评价需要克服因模糊性和不确定性而引起的各目标权重确定的精确性欠佳问题，以及多目标之间的不可公度性和矛盾性问题，引入格序理论，并结合加权Kaufmann距离的概念，以备选方案与正、负加权理想解的综合距离为标准来对方案进行优选。结果表明，利用该方法对水利工程方案进行优选，评价结果客观、合理、有效。

水利工程；方案优选；格序理论；证据理论

0 引 言

水利工程方案优选是从有限的水利工程规划设计或运行管理方案集中选出相对最优方案的过程，其实质就是将多个评价指标问题转换成单个综合评价指标的形式,以便在一维实数空间中对各方案进行分类排序[1]。

目前，国内外有关学者对方案优选进行了大量研究工作，杨增玲等[2]应用序关系分析法和熵值法的综合集成赋权方法进行指标权重确定，采用灰色关联理想解法对黑龙江地区的农作物秸秆综合利用方案进行优选；沈强等[3]将层次分析法和灰色关联分析法相结合，建立了生物质能开发方案优选的数学模型，并将该模型应用于浙江省生物质能开发方案优选中；郑海力等[4]建立了基于灰靶决策与粗糙集的采矿方案优选分析体系模型，并根据粗糙集理论对指标因素进行了约简；徐存东等[5]建立了基于信息熵权的改进TOPSIS综合评价模型，并将该模型用于乌海市摩尔沟河道整治方案优选中；金晶等[6]运用层次分析法构造了水资源配置综合评价指标体系，并结合模糊一致矩阵建立了AHP-模糊决策优选模型；苏生瑞等[7]运用层次分析法对评价方案因子权值进行计算，采用集对分析评价方法，对各方案进行优劣评价；董前进等[8]基于D-S证据理论确定方案权重，实现了对水资源配置方案的优选评价；Hyde K M等[9]运用基于可靠度的多目标决策法对水资源配置方案进行了研究；Saaty T L[10]将AHP法与BP神经网络模型结合，对某项目管理方案进行了评价；Ertugrul I等[11]通过采用模糊AHP法与模糊TOPSIS对比，对设备位置选择方案进行了评价；Ashtian B等[12]采用基于区间值模糊集的可拓TOPSIS法对固体废弃物处理方案进行了评价；Amin A[13]采用模糊TOPSIS多目标决策法对Karun水库调度方案进行了评价。上述研究为方案优选提供了大量可行途径，但均未能很好的解决多目标之间的不可公度性和矛盾性问题，且权重确定方法主观性较强，影响评价结果的可信度。

鉴于此，本文在前人研究的基础上，建立了基于格序理论的水利工程方案优选模型，以期能够较全面、客观地做出方案评价,为水利工程方案优选提供一条新途径。

1 水利工程方案优选

1.1 基本假设

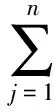
1.2 基于证据理论的权重确定方法

假设Ei(i=1,2,…,n)为在辨识框架Θ下的证据，mi(i=1,2,…,n)为在同一辨识框架Θ上的基本信任分配函数，焦元分别为Ai(i=1,2,…,r)，则任意两个证据Ei、Ej间的距离可以表示为：

(1)

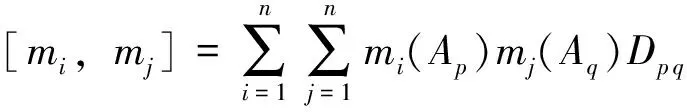
证据距离与证据相似度是一对互补的概念，若证据之间的距离越大，则说明证据之间的冲突越大，相应的证据之间的相似度就越小；反之，则相似度越高。因此，任意两个证据之间相似度可表示为：

(2)

式中Sim(mi,mj)为mi和mj之间的相似度。

当存在多个证据时，该证据与其它证据之间的相似度之和可以表示为整个证据源对该证据的支持程度，表达式为：

(3)

式中Sup(mi)为一个证据Ei在证据源中的支持度。

Sup(mi)越大，说明证据Ei被其它证据支持的综合程度越高，即可认为在证据源中其可信度较高；反之，则表明其在证据源中的可信度较低。

可信度表达式为：

(4)

式中Crd(mi)为一个证据Ei在证据源中的可信度。

在方案优选过程中，一个评价指标的可信度越高，说明在该评价指标下，各方案所能得到的评价指标结果集的可信度就越高，因而该评价指标在评价过程中应该受到重视，被赋予较大的权重，即ωi=Crd(mi)。指标权重计算如下：

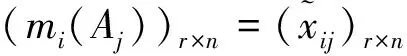
2)由于水利工程方案优选一般有多个评价指标，故用式(3)来求出各个评价指标在评价指标集中的支持度：Sup(m1),Sup(m2),…,Sup(mn)。

3)根据式(4)，将各个评价指标在评价指标集中的支持度转化为各评价指标的可信度Crd(mi)，i,j=1,2,…,n，评价指标的可信度向量为(Crd(m1),Crd(m2),…,Crd(mn))，即评价指标的权重向量为W=(ω1,ω2,…,ωn)。

1.3 方案综合评价方法

基于格序理论的水利工程方案评价计算步骤如下[16]：

1)利用证据理论计算各指标的可信度，确定各评价指标权重W。

2)利用线性变换的规范化处理方法，对指标值矩阵F进行规范化处理并计算加权决策矩阵T=(tij)r×n，其中tij=ωj·xij(i=1,2,…,r；j=1,2,…,n)。

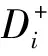
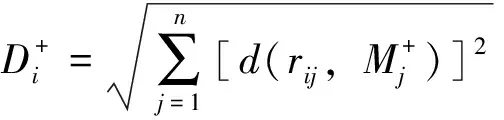
(5)

5)计算评价对象Bi(i=1,2,…,m′)的综合距离：

(6)

式中D为M+与M-之间距离；p为乐观系数，其取值视具体情况而定，一般取0.5。

6)根据Di值的大小，对方案进行优劣排序，Di值越大方案越优，反之越劣。

2 模型应用

2.1 文献资料

本文以文献[17]某流域水电工程投资方案优选为例，主要从经济效益角度出发,对各方案进行优选排序(各方案指标以及指标值见表1)。

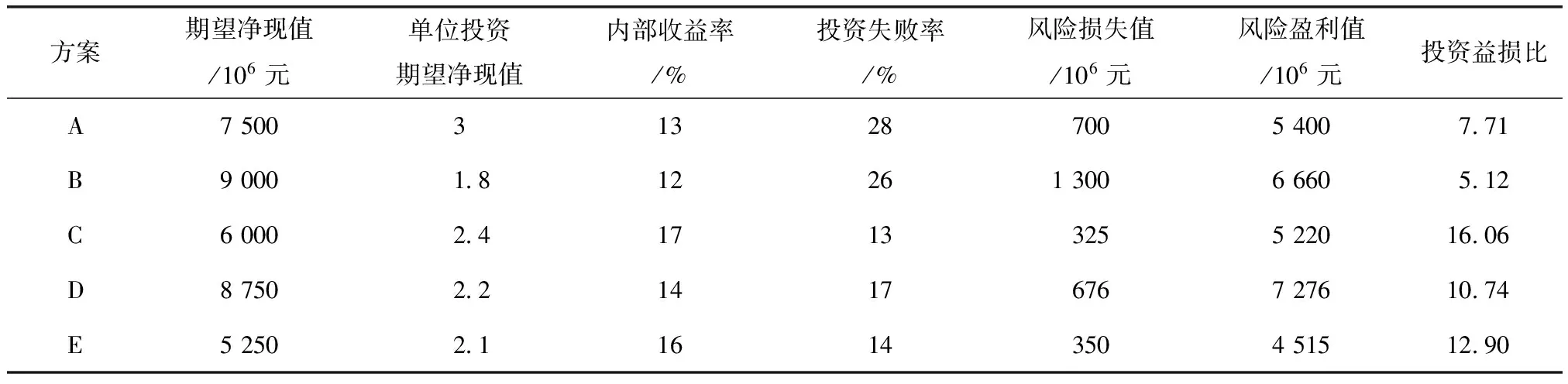
表1 各方案评价指标值

2.2 模型计算

1)确定各评价指标权重。对各方案评价指标的数据进行归一化处理，并根据式(1)，计算各评价指标之间的距离，得到评价指标距离矩阵：

根据式(3)、式(4)，将各评价指标间的距离转化为指标的可信度，从而得到评价指标的权重向量W：W=(0.122，0.171，0.153，0.118，0.124，0.149，0.163)。

2)计算加权决策矩阵。对表1中各方案指标构成的指标值矩阵F进行规范化处理，结合权重向量W，计算加权决策矩阵T=(tij)：

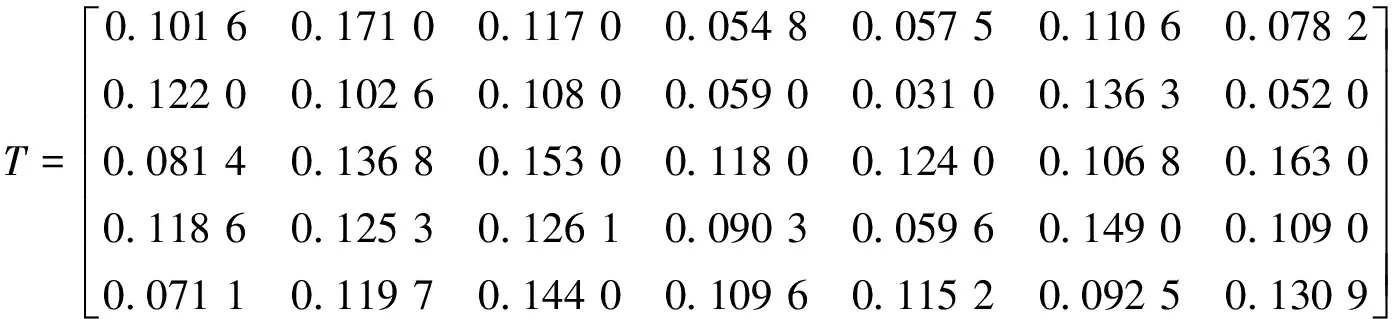
3)根据加权决策矩阵T=(tij)，确定正加权理想解M+和负加权理想解M-。

M+=(0.122 0,0.171 0,0.153 0,0.118 0,0.124 0,0.149 0,0.163 0)

M-=(0.071 1,0.102 6,0.108 0,0.054 8,0.031 0,0.092 5,0.052 0)

4)根据式(5)，得到各评价方案与正、负加权理想解的距离向量为：

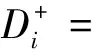
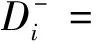
计算出正、负加权理想解的距离为D=0.161 6。

5)本文取乐观系数p=0.5。根据式(6)可得各方案与正、负加权理想解的综合距离向量为：(D1,D2,D3,D4,D5)=(0.342 2，0.160 6，0.812 3，0.514 3，0.609 8)

6)根据Di值的大小，得到各方案优劣的排序：方案C>方案D>方案E>方案A>方案B(>表示优于)。

2.3 结果分析

由上述结果可知，方案C为最佳方案，方案B为最劣方案。由表1数据分析各方案优劣排序的合理性，发现：方案C的多项指标(投资益损比、内部收益率、投资失败率、风险损失值4项指标)均处于最优值，期望净现值、风险盈利值与单位投资期望净现值这3项指标处于较优值，综合评价方案C为最优方案是合理的；方案B的多项指标(单位投资期望净现值、内部收益率、风险损失值、投资益损比与投资失败率5项指标)均处于最劣值或次劣值，期望净现值与风险盈利值这2项指标处于较优值，综合评价方案B为最劣方案也是合理可信的；方案D、方案E与方案A的各项指标值均介于最优值与最劣值之间，综合评价方案D>方案E>方案A是合理的。

2.4 评价结果对比

为了检验本文所建模型的准确性，通过与文献[17]结果对比，发现两者结论完全一致(表2)，这验证了本模型的准确性。同时，文献[17]采用专家打分法对方案进行优选，其计算结果存在一定的主观性，而本文是基于格序理论对评价指标客观赋权，因此本文所建模型计算结果更加合理。

3 结 论

1)本文应用证据理论中的证据距离思想来对各方案中评价指标的已知信息进行挖掘和融合，基于各评价指标可信度确定相应权重，所得结果较为客观，能较好的解决因模糊性而引起的精确性欠佳问题，提高方案评价结果的可信度。

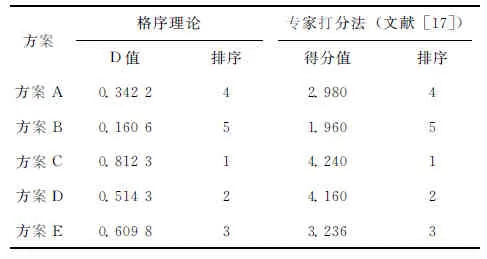
表2 模型评价结果对比

2)在传统方案优选过程中，只考虑评价方案与正理想解的相似度或者隶属度，以单一标准来对方案进行优选。本文取正、负加权理想解为顶元素和底元素，构造概念格，以评价方案与正、负加权理想解的综合距离为标准来对方案进行优选，使得优选结果更全面。

3)应用加权Kaufmann距离来刻画各评价方案与理想解之间的差异，比一般的格序决策评价方法所用的Hamming距离更合理，更能形象地反映其真实差异。

[1]薛仓生,金菊良,魏一鸣.水利工程方案优选的投影寻踪方法[J].长江科学院院报,2005,22(4):80-83.

[2]杨增玲,楚天舒.灰色关联理想解法在秸秆综合利用方案优选中的应用[J].农业工程学报,2013,29(20):179-191.

[3]沈 强,姚炎明,何 勇. 基于灰色多层次综合评判模型的生物质能开发方案优选[J].农业工程学报,2012,28(17):179-185.

[4]郑海力,陈 新,周 勇,等.基于灰靶决策理论与粗糙集的采矿方案优选[J].矿业工程研究,2013,27(1):1-6.

[5]徐存东,翟东辉,张 硕,等. 改进的TOPSIS综合评价模型在河道整治方案优选中的应用[J].河海大学学报：自然科学版,2013,36(3):222-228.

[6]金 晶,唐德善. 基于AHP-模糊决策模型的水利工程方案优选[J].水电能源科学,2013,(5):33-35.

[7]苏生瑞,张其伟,景积仓,等. 基于集对分析方法的山区高速铁路线路方案优选研究[J].工程地质学报,2011,(5):764-770.

[8] 董前进,陈森林,张柳波,等.基于D-S证据理论的水资源合理配置方案综合评价[J].数学的实践与认识,2011,41(5):26-30.

[9] Hyde K M, Maier H R, Colby C B.Reliability-based approach to multicriteria decision analysis for water resources[J]. J Water Resour Plan Manage,2004,130(6):429-438.

[10] Saaty T L. Decision making:the analytic hierarchy and network processes (AHP/ANP)[J]. J Syst Sci Syst Eng,2004,13(1):1-35.

[11] Ertugrul I, Karakasoglu N.Comparison of fuzzy AHP and fuzzy TOPSIS methods for facility location selection[J]. Int J Adv Manuf Technol,2008,39:783-795.

[12] Ashtian B, Haghighirad F. Extension of fuzzy TOPSIS method based on interval-valued fuzzy sets[J]. Applied Soft Computing,2009,9:457-461

[13] Amin A.Fuzzy TOPSIS multi-criteria decision analysis applied to karun reservoirs system[J]. Water Resour Manage,2011,25:545-563

[14] Nakamura K. Preference relations on a set of fuzzy utilities as a basis for decision making[J]. Fuzzy Sets and Systems,1986,20(2):147-162.

[15] 孔 峰.模糊多属性决策理论、方法及其应用[M].北京:中国农业科学技术出版社,2008.

[16] 吴先聪,刘 星.基于格序理论的管理者绩效评价方法[J].系统工程理论与实践,2011,31(2):239-246.

[17] 黄志中,周之豪.水电工程投资的多目标风险决策[J].水利经济,1994,(2):10-13.

Optimizing choice of water resource project schemes based on lattice-order theory

WEI Guang-Hui

(School of Water Resources & Civil Engineering, Xinjiang Agricultural University, Urumqi 830052,China )

Comprehensive assessment of water resources projects scheme is to overcome the problems that target weight is poor caused by the ambiguity and uncertainty of certain accuracy and multiple targets is not commensurable and contradictory. The lattice-order theory was introduced, based on the concept of weighted Kaufmann distance, choose positive, negative weighted ideal solution integrated distance as the standard to optimize the scheme. The results show that, the evaluation result is objective,reasonable and effective to optimize the water conservancy project by the method.

water resources project; optimization choice; lattice-order theory; evidence theory

10.13524/j.2095-008x.2014.01.004

2013-12-09;

2013-12-22

新疆水文学及水资源重点学科项目(XJSWSZYZDXK20101202)

魏光辉(1981- )，男，新疆石河子人，高级工程师，在读博士研究生，研究方向：干旱区水资源利用，E-mail:xndwgh@sina.com。

TV212

A

2095-008X(2014)01-0018-05