东北寒区逊毕拉河水文要素时序演变特征分析
李祥龙, 吴志琴, 宋小雨
(1.黑龙江省九〇四水文地质工程地质勘察院,哈尔滨 150027,2.黑龙江省水利科学研究院,哈尔滨 150080)
东北寒区逊毕拉河水文要素时序演变特征分析
李祥龙1, 吴志琴2,*, 宋小雨1
(1.黑龙江省九〇四水文地质工程地质勘察院,哈尔滨 150027,2.黑龙江省水利科学研究院,哈尔滨 150080)
利用最小二乘原理建立多项式的系数矩阵,结合Origin软件对实测的2009年逊毕拉河流域吴家堡站水文要素值日平均流量进行了多项式拟合,拟合结果表明:相对误差的最大值为0.025%,最小值为0.001 4%,平均值为0.013 6%,其计算值接近实测值,因此用构造的水位~流量关系曲线可以准确、可靠地描述东北寒区逊毕拉河水位流量时序演变规律。
中小河流;水文要素;时序演变;寒区
0 问题的提出
逊毕拉河又称“逊别拉河”,是黑龙江上游一条较大的支流,位于黑龙江省黑河市境内,是典型的东北寒区中小河流。该流域年径流总量为30.95×108m3,水能蕴藏量为20.37×104kW,经东北水利勘测设计院勘测规划,在逊毕拉河最大支流沾河上可修建4座梯级水电站,流域内可规划4处灌区工程、3处涝区工程、5处水库工程、3处河道整治工程[1]。流域径流量变化特征会直接影响水利工程的规模和水资源的合理配置,且水位和流量的预报在水利水电工程规划、设计与施工过程中一直是一个重要的课题[2-4],为了研究逊毕拉河水位~流量时序演变特征,本文利用最小二乘原理建立多项式的系数矩阵,结合Origin软件对实测的2000~2009年逊毕拉河吴家堡站实测的日平均流量和日平均水位的数值进行了分析,得出逊毕拉河水位~流量时序演变规律曲线,为合理配置逊毕拉河流域水资源、研究东北寒区中小河流演变规律提供参考[5]。
1 逊毕拉河概况
逊毕拉河发源于小兴安岭北坡,河源位于126°30′E,49°30′N;河口位于128°59′E,49°25′N,流域面积为15 846.6 km2,河长251 km,流经孙吴、逊克两县,于逊克县车陆乡西双河村流入黑龙江,沿途有多条支流汇入,其中较大的支流有辰清河、沾河等[1]。
2 流量变化规律分析
根据逊毕拉河吴家堡站流量系列资料(表1),可见逊毕拉河1、2、3、11、12月流量很小,流域出现部分冻结或连底冻。而最大流量出现在4~8月,其流量占全年的93.5%。9~10月流量开始减小,水位下降。
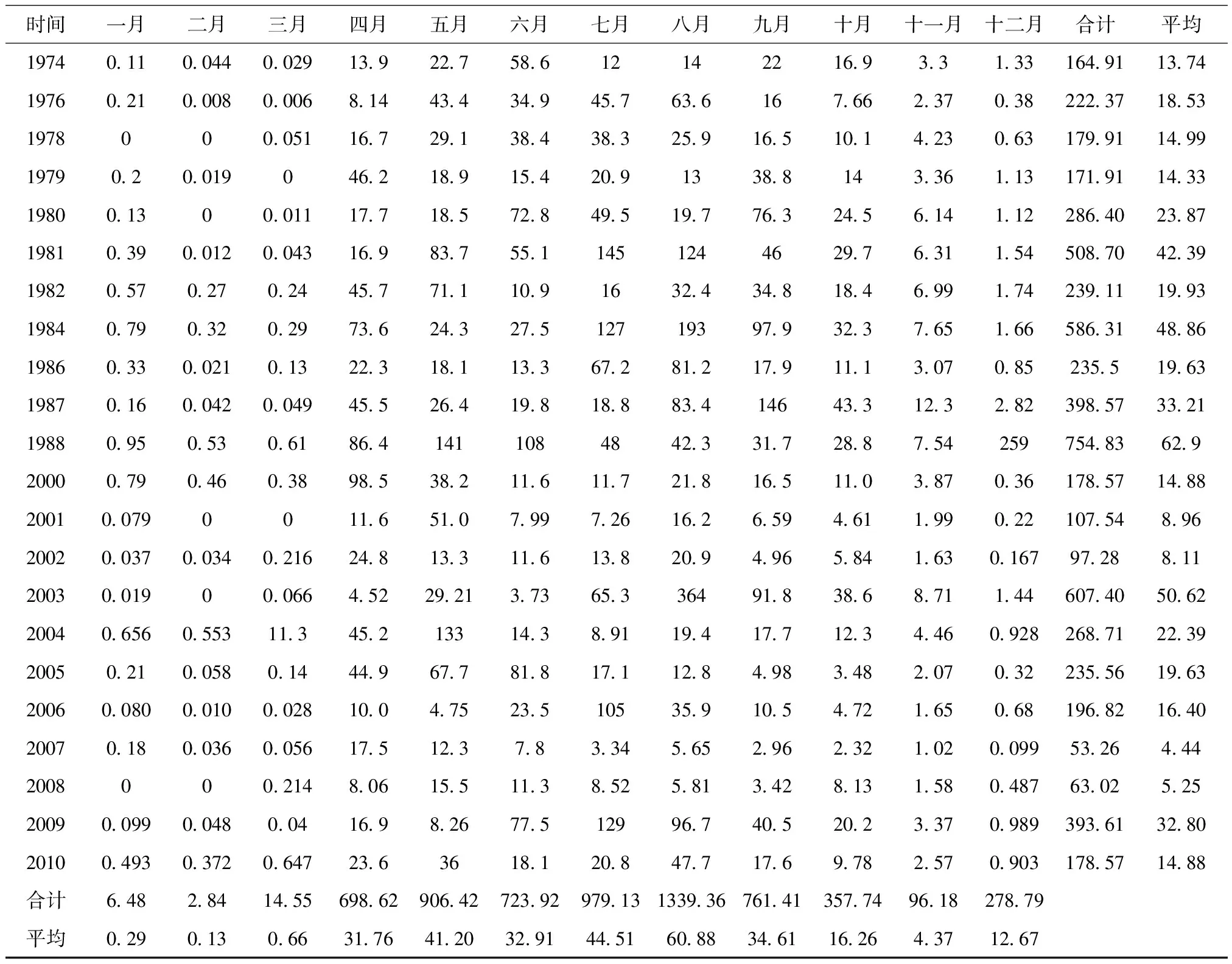
表1 逊毕拉河吴家堡站月平均径流量统计表
为分析逊毕拉河的流量年际变化特征,本文选取变差系数Cv、年际比值Ka和年际不均匀系数A进行分析。计算公式[6-7]为:
(1)
式中n为观测年数;Ki为第i年年径流量与正常年径流量的比值。
(2)
式中Rmax为变量最大值;Rmin为变量最小值。
(3)
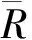
计算结果见表2。

表2 逊毕拉河吴家堡站流量年际变化参考值
由表2可见,逊毕拉河吴家堡站径流量年际变化大,且变化不均匀。因此研究该河流水文要素时序演变特征尤为重要。
3 水位流量关系分析
3.1 流量与水位的相关性分析
采用SPSS软件[8]对2009年逊毕拉河吴家堡站实测的日平均流量和日平均水位进行相关性分析,得出其相关系数r=0.930,显著性水平为0.000,流量与水位的相关性十分显著。
3.2 水位流量关系曲线多项式拟合分析
3.2.1 曲线拟合的最小二乘原理
多项式拟合可以对零点误差进行补偿(包含常数项),而且随着阶数的提高,拟合的精度还会逐步提高[9]。稳定的水位流量关系是一种单值曲线,因而可以用带一个未知数的多项式来逼近,于是,流量可以表示为水位的多项式函数。其形式如:
(4)
式中a0,a1,a2,…,am为多项式系数。
用式(4)来拟合n对数据{(qi,Zi)},(i=1,2,…,n) ,节点qi处测量值与计算值通常不等,其差值可用残差表示:
(5)
残差的大小是衡量拟合好坏的一个重要因素,最小二乘法的基本思想就是对于所有给定的数据点,使残差的所有平方和最小,即:
(6)
将Φ视为系数式(4)aj的函数:
(7)
上述数据拟合的问题归结为求多元函数的极值问题,欲使Φ取得极小值,则a0,a1,…,am必须满足:
(8)
对式(6)求偏导数可得到:
(9)
即
(10)
令
则式(10)可表示为:

(11)
这是一个m+1阶对称的线性方程组,其矩阵形式为:
(12)
传统上用高斯—若当消去法对主方程(12)求解,得到多项式拟合函数(4)的n项系数ai(i=0,1,2,…,n),并得到拟合函数。本文采用Origin软件对散点图进行多项式拟合,可直接得出拟合函数、残差和标准偏差等值。
3.2.2 多项式拟合的实现
为了研究流量与水位关系曲线,采用Origin软件对逊毕拉河吴家堡水文站2009年实测的日平均水位和日平均流量的数据分别进行2、3、4次曲线拟合, 曲线拟合结果见图1~图3。
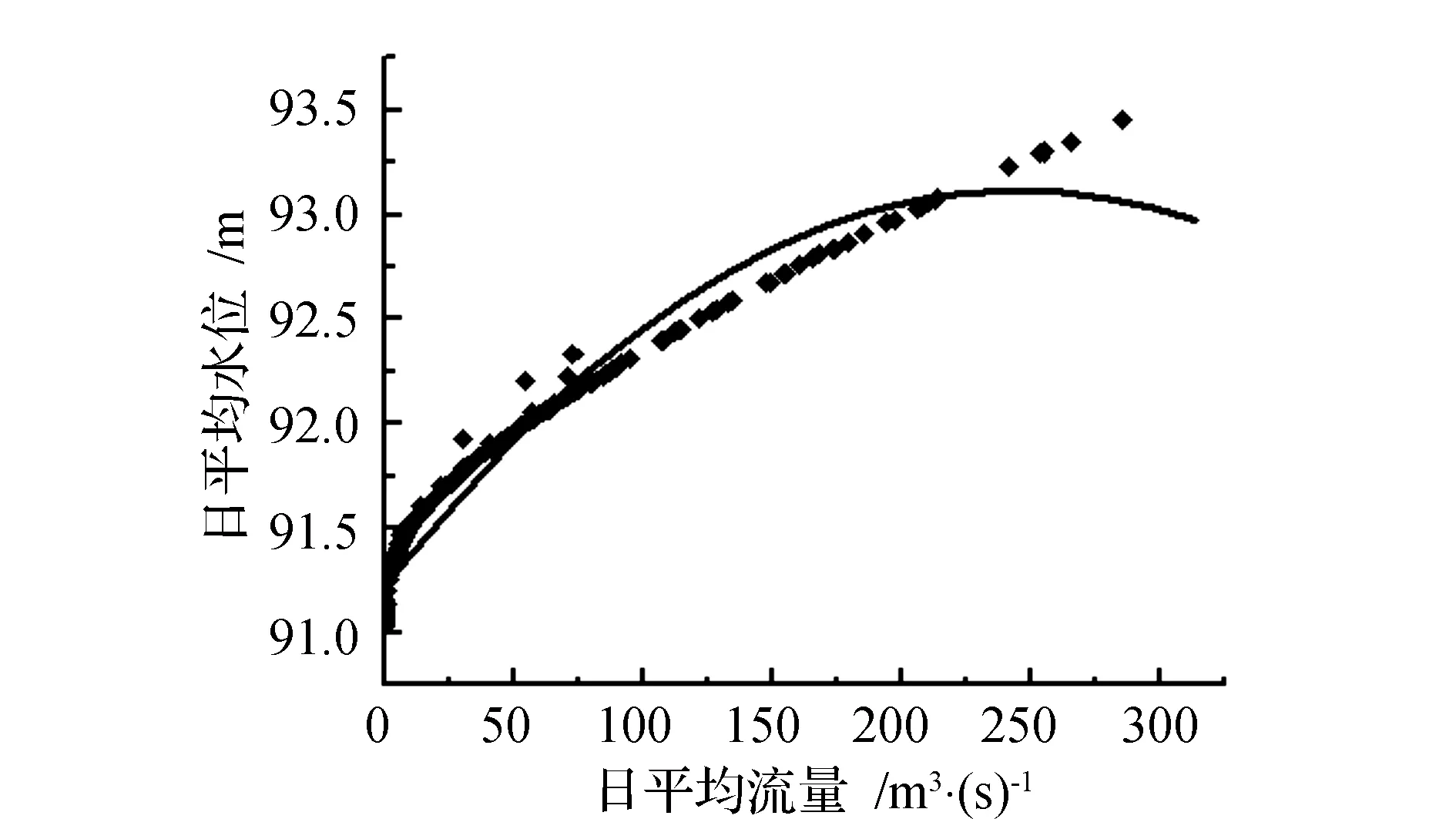
图1 2次拟合水位流量关系图Fig.1 Stage-discharge chart of 2 times polynomial curves
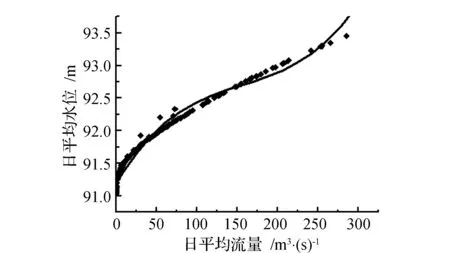
图2 3次拟合水位流量关系图Fig.2 Stage-discharge chart of 3 times polynomial curves
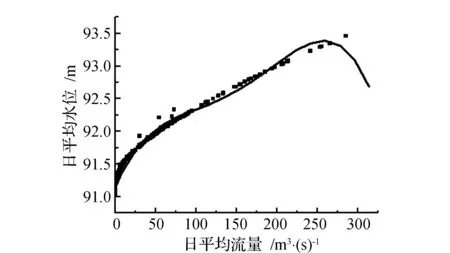
图3 4次拟合水位流量关系图Fig.3 Stage-discharge chart of 4 times polynomial curves
由图1、图3可见,随着平均流量的增加,其水位有时增大,有时减小,与实际情况不符。图2符合实际情况,因此,3次拟合曲线:
Z=91.292 67+0.021 15q-1.101 76E-
4q2+2.345 8E-7q3
(13)
可作为逊毕拉河水位流量关系曲线。
4 结果与结论
为了验证拟合曲线的精度,将2009年5月实测的流量值代入3次拟合曲线,计算对应的水位、绝对误差和相对误差,结果见表3。
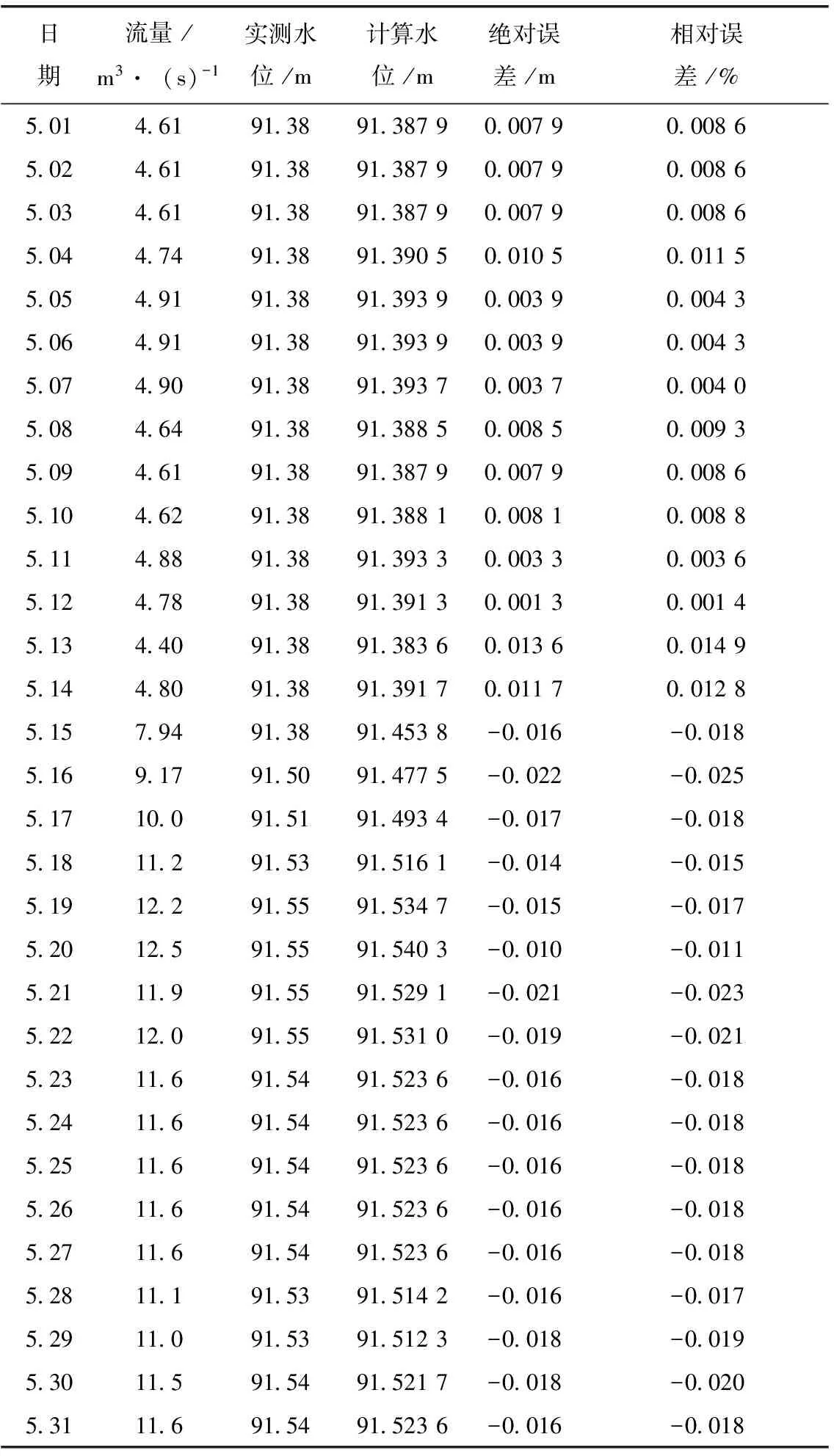
表3 逊毕拉河流域吴家堡水位流量拟合结果
由表3可见,3次拟合曲线的绝对误差和相对误差都很小,绝对误差最大值为-0.022 m,最小值为0.001 3 m,平均值为0.012 4 m;相对误差的最大值为0.025%,最小值为0.001 4%,平均值为0.013 6%。本文构造的水位流量关系曲线误差在允许范围内,因此,可以描述逊毕拉河水位~流量时序演变规律。同时,在全球气候变化背景下,研究寒区中小河流水文要素时序演变特征对维护寒区水源涵养功能、保障寒区中小河流域水域安全和促进社会经济发展具有指导意义。
[1]唐晶云,王荣臣.逊别拉河流域水资源开发前景[J].东北水利水电,1997,(6):34-40.
[2]王春霞.稳定水位流量关系加权有约束优化模型及其求解[J].水利水电,2008,(1): 1-6.
[3]温维超.大华电站水位流量关系的确定[J].云南水力发电,2002,(18):25-26.
[4]李致家,韩从尚.河道流量和水位模拟的综合法介绍[J].人民黄河,1990,12(2):16-20.
[5]李欣欣,孙思淼.额穆尔河径流特征及其与气象因素的相关性分析[J].黑龙江水专学报,2009,36(2):125-127.
[6]董晓辉,姚治君,陈传友.黄河源区径流变化及其对降水的响应[J].资源科学,2007,29(3):68-73.
[7]李道峰,田 英,刘昌明.GIS支持下的黄河河源区降水径流要素变化分析[J].水土保持研究,2004,11(1):144-155.
[8]东方人华.统计基础与SPSS11.0入门与提高[M].北京:清华大学出版社,2004.
[9]李守军,高 磊,徐立中,等.水位流量曲线BP神经网络逼近与多项式拟合对比[J].水电自动化与大坝监测,2009,33(1):5-9.
[10]戴凌全,戴会超,蒋定国,等. 基于最小二乘法的河流水位流量关系曲线推算[J].人民黄河,2010,31(9):37-39.
Analysis of the time series evolving feature hydrologic factors of Xunbila River in cold region of Northeast
LI Xiang-Long1, WU Zhi-Qin2,*, SONG Xiao-Yu1
(1. Heilongjiang Province 904 Hydrogeology Engineering Geologic Investigation Institute, Harbin, 150027, China; 2. Heilongjiang Provincial Hydraulic Research Institute, Harbin 150080,China)
Basing on the datas of hydrologic factors Xunbila River in 2009,make a polynomial fitting with the software of microcal origin.The result showed that the maximum absolute deviation is 0.025%,the minimum is 0.001 4%,the average is 0.013 6%, and all of the water level value calculated are closed to actual value.Consequently,the curves of water level-discharge relation can describe accurately and reliably the development regularity of water level-discharge relation in cold region river of northeast.
small river;hydrologic factors;time series evolution;cold region
10.13524/j.2095-008x.2014.01.007
2013-11-27
http://www.cnki.net/kcms/detail/23.1566.T.20140107.1320.002.html
李祥龙(1985-),男,黑龙江齐齐哈尔人,助理工程师,研究方向:地下水环境;*通讯作者:吴志琴(1984-),女,四川达州人,助理工程师,硕士,研究方向:寒区水利工程。
P333.9
A
2095-008X(2014)01-0032-04

