ADCP实测流量不确定度评定及测次控制指标的确定

钱学伟

(黑龙江省水文局，哈尔滨 150001)

ADCP实测流量不确定度评定及测次控制指标的确定

钱学伟

(黑龙江省水文局，哈尔滨 150001)

提出了一种计算ADCP实测流量标准差模型，详细阐述了ADCP实测流量不确定度间接评定的程序和方法，并与直接评定法进行对比。引用黄河宁报告的资料数据，做了一个算例。从计算标准差的最大残差法出发，分析了ADCP法流量测验测次控制指标和精度指标的关系，提出一种新的测次控制指标的确定方法。

ADCP；实测流量；标准差；不确定度；测次控制指标

0 引 言

声学多普勒流速剖面仪(Acoustic Doppler Current Profiler,ADCP)是20世纪80年代初发展起来的一种新型测流仪器。ADCP利用声学多普勒效应原理，在不扰动流场的情况下测量水流剖面流速，有测验历时短、测验精度高、测速范围大等特点。目前，ADCP不仅广泛应用于海洋和河口的流场结构调查及流量测验、海洋资源的勘探及开采，而且在地表水文测验中也得到较广泛应用，为防汛抢险做出了贡献。

对ADCP测量结果进行误差分析和评定是提高测量质量，改进测量方法和仪器性能，有效使用测量数据所必需。针对ADCP的测量误差，前人已经做了大量工作。文献[1]、[2]比较全面地讨论了ADCP测流的系统误差和随机误差，指出了各种误差源，给出了系统误差的定量分析和订正方法，估计了各种随机误差，并提出了流量随机误差估算方法。文献[3]主要讨论了系统误差，给出了换能器安装角度、罗经偏角、采用固定声速等系统误差产生原因及订正方法。文献[4]研究了JANUS配置的测速设备在大倾角状态下的误差，提出了修正公式。文献[5]提出了ADCP换能器安装角的计算方法。文献[6]、[7]提出了ADCP实测流量随机不确定度的预测模型和最大相对误差预测模型，特别是在模型中考虑了表层和底层盲区流速插补引起的误差以及测船走航过程中船速比对单砰标准差的放大作用。

本文根据不确定度的概念及评定方法，对ADCP实测流量进行评定；提出了一个概括性较强、较为符合实际的随机误差估算模型；阐述了用最大误差计算标准差及ADCP测验测次控制指标问题。

1 ADCP测流原理

ADCP测流原理包括4个方面：①ADCP的基本原理；②ADCP信号发射和接收原理；③信号处理原理；④流量计算原理。其中②、③不在本文讨论之列，有兴趣的读者可参阅文献[1]、[2]等。

河流中存在着大量散射体，如悬移质泥沙颗粒、气泡、浮游生物等。当ADCP向河水介质发射声波时，这些散射体将会对声波产生散射，形成体积混响。设ADCP向水中发射频率为fo的单频信号，声波在河水中传播时，有一部分能量被河水中的散射体散射回来。换能器接受这些回波信号，经处理后，可测其频率为fr。根据多普勒频移原理，当声源(或接收器)与散射体有相对运动时，则必有fr≠f0,其差fd=fr-f0即多普勒频移，可以证明：

(1)

式中α为波束俯角；v为声源(或接收器)的水平相对速度；C为水中声速。

为了测量水流速度，ADCP需要同时向河水介质发射4个波束的声波脉冲信号，每个声波脉冲的传播方向与垂线夹角为φ,ADCP沿这4个方向发射的声波波束称为JANUS结构。4波束 正交配置的ADCP通常每个波束与水平面夹角为60°，相邻两波束水平投影的夹角为90°，在作用深度范围内，每个波束都能测得流速分量，4个波束可测得4个流速分速度。通过矢量合成可得流速矢量。

船载ADCP是测船横渡过程中完成河道流量测量的。ADCP通过水跟踪求得微断面上各深度单元的流速，通过底跟踪求得测船航速，利用测深仪可求得各微断面水深。

通过河道任一过水面积S的流量基本计算公式为：

(2)

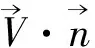
(3)

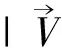
假定ADCP实测断面与水流垂直，式(2)可变为：

(4)

由式(2)还可以演变为另一种流量计算公式[1]：

(5)

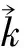
由矢量混合积的性质，即当3个矢量次序不变时，连接它们之间的叉积与点积符号可以交换，式(5)可变为：

(6)

令

则

又令

(7)

(8)

则

(9)

以上诸式中，m为微断面数；n为深度单元数；fj为第i个微断面中第j个深度单元的f值。

本文采用式(4)作为ADCP实测流量计算公式，并据此应用随机误差传播公式，建立实测流量随机误差估算模型。当然，也可以用式(9)计算实测流量估算总随机误差[1]。

2 实测流量标准差计算

2.1 标准差的直接计算

河道流量测验属于间接测量。流速仪法通过对流量的组成因素，诸如流速、水深、河宽的测量，按流量计算公式求得总流量。传统流速仪法，由于测线、测点多，耗费时间长，一份流量成果只能测一次，即所谓单次流量。在评定实测流量精度时，只能用间接方法，通过流量计算模型，按照标准差计算规则，求得单次流量标准差。

用ADCP法测流，在测船从此岸航行到彼岸的过程中就完成了一次流量测验，耗时很短，特别是在大江大河上抢测洪水时，更能显示出ADCP测验历时短的优点。因此，为取得一份流量成果，可以通过多次流量测验，然后取其平均值，作为最后流量值。假如在整个测流过程中， 水位变化在允许范围内，那么这种测量过程，相当于用同一台仪器对同一流量独立地重复测量，因此实测流量标准差可以直接计算。

设一份流量成果，测量n次流量Q1，Q2，…，Qn。对该系列可计算其均值：

(10)

并用贝塞尔公式计算标准差：

(11)

(12)

黄河宁[7]曾于2003年12月10日在美国加利福尼亚州Imperial Irrigation District灌渠Spruce weir站，用微型ADCP进行4组流量测验试验。测验期间渠道平均水深0.93 m，水面宽13.5 m。

微型ADCP主要性能指标是：系统频率为2 400 kHz，盲区为3 cm,水跟踪砰速率为48 Hz，底跟踪砰速率为2 Hz。测验中参数定为：换能器入水深度为4.5 cm，单元长度为10 cm，单元数目为7，流速测验单砰标准差为40.2 cm/s。

本文以黄河宁的这4组流量测验试验数据作为计算标准差和评定不确定度的算例，简称4组试验。4组试验的主要数据摘自文献[7]。实测流量标准差计算结果见表1。

表1 ADCP实测流量标准差计算成果

2.2 标准差的间接计算

ADCP实测的一个流量系列中的任意一次流量属于单次流量，可利用流量计算模型求得单次流量标准差。

对式(4)离散化，可得：

(13)

式中下标i表示与微断面有关的参数;下标j表示与微断面中深度单元有关的参数；Dc为单元长度；Vij为ADCP实测的i微断面j单元流速，为Δt时间(砰集合时间步长，亦即采样步长)内的平均流速；λ为深度单元平均流速系数，当利用幂函数对表层和底层盲区进行流速插补时，λ由下式计算[8]：

(14)

式中H为微断面处水深;b为幂函数指数；Z1为河底至离河底最近处有效单元下边界的距离；Z2为河底至第1个单元上边界的距离。

引进微断面平均流速[8]:

(15)

(16)

式(16)与流速仪法流量计算公式颇有相似之处，VbiΔt相当于微断面宽度，HiVi相当于微断面单宽流量。

对式(16)进行求函数标准差运算[9]。假定：①微断面中测船航速、水深和流速的随机误差相互独立，且各微断面之间相应测量值的随机误差也相互独立；②不考虑时间微元Δt的误差；③各微断面航速相对标准差、水深相对标准差和流速相对标准差相等；④各微断面流量相等；⑤不考虑抽样误差。于是可得：

(17)

进而：

(18)

式中：

这里关键是计算微断面平均流速标准差。为此对式(15)进行标准差运算，并假定各水深单元流速的随机误差相互独立，且各水深单元绝对流速单砰标准差相等，得：

(19)

式中N为单元流速测验砰个数，N=RΔt,R为砰速率。

文献[8]指出，ADCP在走航过程中进行测验，这时绝对流速Va的单砰标准差并不等于相对流速Vr(相对于ADCP的流速)的单砰标准差σ(亦即ADCP的单砰标准差)，而且与航速Vb与绝对流速Va之比值有关。在假定测船航迹与水流相垂直的条件下，由：

(20)

求得绝对流速单砰标准差与相对流速单砰标准差的关系为[8]：

(21)

(22)

(23)

式中μ为走航测验ADCP单砰标准差放大系数。

由式(19)、式(22)可得微断面平均流速相对标准差：

(24)

于是式(18)成为：

(25)

在建立模型(25)时用到5个假定，其中假定①～②是水文测验误差评定中通常作法。现就假定③和④略加阐述。

关于假定③。赫尔西[10]曾针对流速仪法分析了假定部分流量相等对计算流量不确定度的影响。他选取测速垂线为14～58条，流量为9.52～420 m3/s共11次流量资料，分别计算了假定部分流量相等时的流量不确定度和部分流量不相等时的流量不确定度。结果发现两者之差仅为0.17%～5.80%，可谓甚小。由于ADCP法与流速仪的流量计算原理本质上是一致的，所以在计算ADCP实测流量标准差时，为简化计算，采用各微断面流量相等的假定是可以接受的，同样不会对流量标准差的计算产生较大影响。

关于抽样误差。流速仪法实测流量总误差的主要误差分量是Ⅰ型误差、Ⅱ型误差和Ⅲ型误差[10-12]。Ⅰ型误差是指有限测速历时产生的测速误差，它发生在测点上，传播到垂线平均流速和断面流量上。Ⅱ型误差是指垂线平均流速计算规则或有限测点产生的垂线平均流速误差，它发生在测线，传播到断面流量上。Ⅲ型误差是指有限垂线数产生的断面流量误差，表面上看它发生在断面上，实质上它产生于部分流量，传播到断面流量上。这3种类型的误差都是抽样误差。ADCP法测流也应当存在抽样误差，因为微断面数对应于流速仪法的垂线数，深度单元数对应于流速仪法的测点数，单砰采样步长对应于测速历时。文献[1]在讨论ADCP法实测流量的不确定度时，引入由于相邻微断面之间水深和流速的非线性变化而引起的不确定度，并且与微断面数有关，随着微断面数的增多，该项不确定度减小。实际上，这项不确定度表示的就是由于微断面数有限引起的类似于流速仪法Ⅲ型误差的抽样误差。文献[13]在谈到ADCP流量测验误差来源时，将“流速脉动引起的流速测量误差”列入其中，其实这项误差就是由有限测速历时引起的抽样误差。至于脉动误差的大小，有的认为其标准差可达8%～12%[2]，有的认为由于测流时测船横渡时间大于紊流时间尺度，紊流速度在流量计算中对流速进行平均后将很小，因此可忽略紊流的影响[6]，即忽略脉动误差的影响。

鉴于在ADCP实测流量随机误差估算模型中应否考虑抽样误差、抽样误差如何定量均需通过试验研究取得足够数据后确定，其次，本文有意将ADCP实测流量标准差的直接算法和间接算法进行比较，而直接算法中的标准差是不含抽样误差的。因此，本文推荐的随机误差模型中未考虑抽样误差。一旦有试验数据表明应考虑某一项抽样误差，只要在式(25)中加入即可。

应用模型(25)间接计算的实测流量标准差见表1。

3 实测流量不确定度评定

不确定度在水文测验中已得到广泛应用。现根据文献[14]中的概念和评定程序，来评定ADCP实测流量不确定度。

用标准差表征的不确定度，称为标准不确定度[14-16]。标准不确定度的评定方法有A类评定和B类评定。

A类评定是用统计分析法评定其标准不确定度u，等同于由系列观测值直接计算的标准差S，即u=S。

B类评定不用统计分析法，而是用其他方法估计概率分布或分布假设来评定标准差并得到标准不确定度。

3.1 实测流量不确定度的直接评定

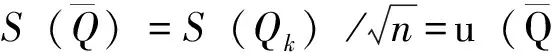
3.2 实测流量不确定度的间接评定

3.2.1 合成标准不确定度

因为标准不确定度就是标准差，所以标准不确定度的合成问题实际上就是随机误差的传播问题。于是式(25)可写成：

(26)

其中：

(27)

(28)

(29)

以上诸式中，uc(Q)为实测流量合成相对标准不确定度；u1(Q)、u2(Q)、u3(Q)分别为航速、水深和流速产生的不确定度分量；urel(Vb)、urel(H)、urel(V)分别为航速、水深和流速的相对标准不确定度。

urel(Vb)、urel(H)和urel(V)原则上可采用A类评定，也可采用B类评定。下面以文献[7]提供的4组实测流量数据计算其合成标准不确定度。4组实测流量的有关参数见表2。计算中还将用到的数据有：Dc=0.1 m，R=48，Δt=1 s，平均水深H=0.93 m，Z1=0.1 m，Z2=0.78 m，b=1/6。

航速标准不确定度采用B类评定。美国地质调查局认为航速不确定度为0.89%[1],现采用该值作为航速相对标准不确定度，urel(Vb)=0.89%。

水深标准不确定度采用B类评定。ADCP法测流时，水深用与高分辨率换能器相连结的回声测深仪测量，厂家给出的精度是不超过示值水深的±0.5%[1]。由此可认为测深误差在[-0.5%，+0.5%]区间内呈均匀分布，而随机变量服从均匀分布u[-a,a]时，其标准差为：

(30)

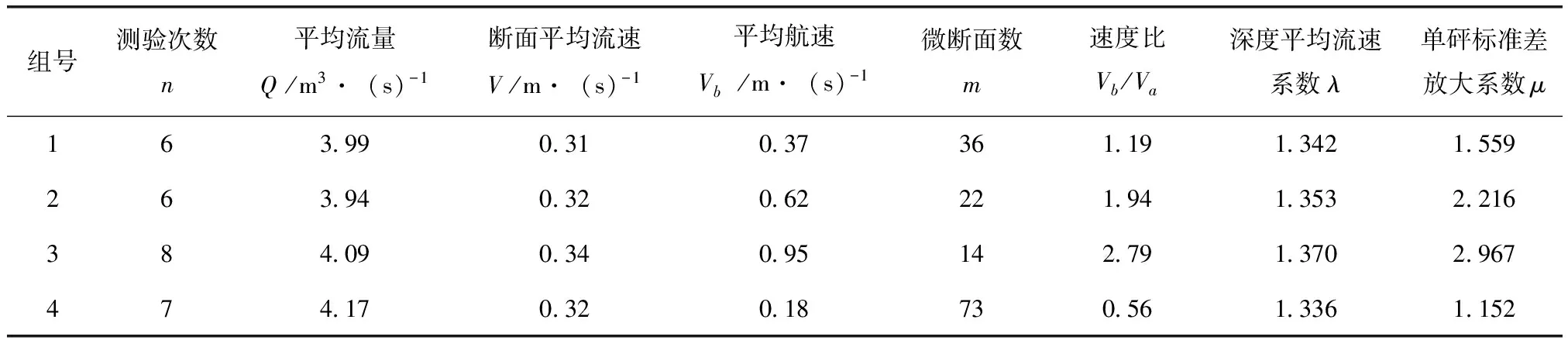
表2 实测流量参数

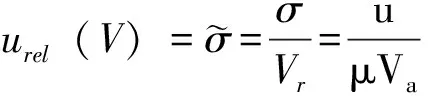
由式(26)～式(29)可求得4组试验的合成标准不确定度，见表3。

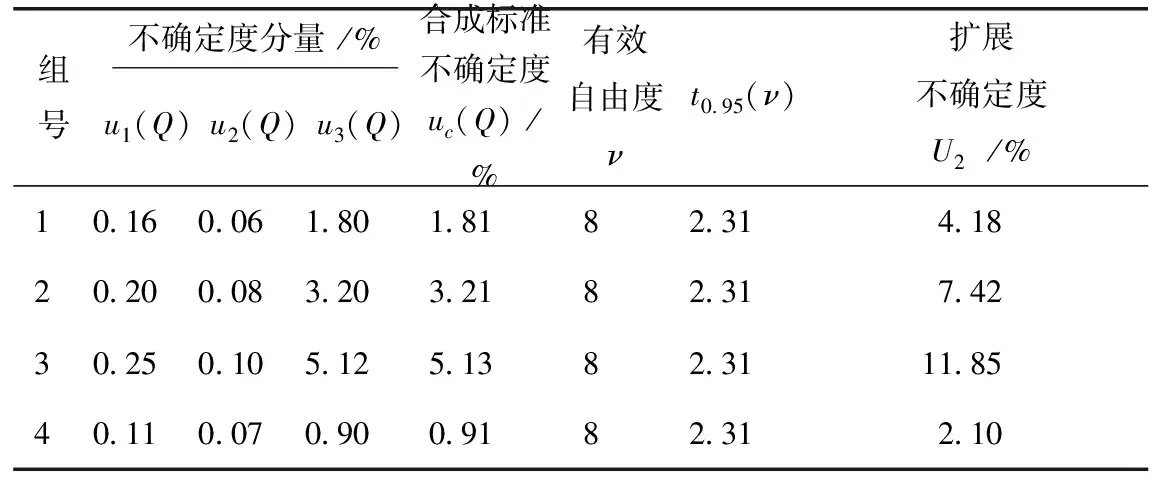
表3 实测流量不确定度评定结果

3.2.2 合成标准不确定度的自由度

由上节计算可知，ui(Q)(i=1,2,3)属于B类评定的不确定度分量。对于A类评定的不确定度，其自由度可直接用韦尔奇-萨特思韦特(Welch-Satterthwaite)公式[15-16]:

(31)

可以证明，对于由形如式(16)的函数式求得的合成标准不确定度模型，式(31)中的标准不确定度可以用相对标准不确定度代替。而对于B类评定的不确定度，需先用式(32)估算不确定度分量的自由度：

(32)

式中Δu(xi)为标准不确定度u(xi)的不确定度；Δu(xi)/u(xi)是标准不确定度u(xi)的相对标准不确定度，这是一个主观量，可按所依据的信息来源的可信程度来决定Δu(xi)/u(xi)。

本例u(Vb)、u(H)来自美国地质调查局的报告[1]，u(V)来自黄河宁的试验报告[7]，可大致认定u(Vb)、u(H)和u(V)的不可靠程度均为25%，即Δu(Vb)/u(Vb)=Δu(H)/u(H)=Δu(V)/u(V)=0.25，相应的自由度为νVb=νH=νV=8。再由式(31)求得合成标准不确定度的自由度，见表3。

3.3 扩展不确定度

尽管合成标准不确定度可以广泛用于表示测量结果的不确定度，但是流量测验，特别是汛期江河的洪水流量测验，涉及抗洪抢险和人民生命财产的安全，需要提供一个不确定度的测度，以给出测量结果的区间，合理赋于被测流量的值分布的大部分可望含于其中。这一不确定度的测度称为扩展不确定度或展伸不确定度，扩展不确定度U由合成标准不确定度uc(Q)乘以包含因子k得到：

U=kuc(Q)

(33)

当Q接近正态分布时，包含因子等于t分布临界值，即：

(34)

式中p为置信概率，水文测验中通常取p=95%;ν为合成标准不确定度uc(Q)的有效自由度。

当有效自由度无法决定时，水文测验中包含因子通常直接取k=2。4组试验的包含因子和扩展不确定度见表3。

3.4 不确定度直接评定与间接评定的关系

如2.1节和3.1节所述，若ADCP为取得一份流量成果测量了n次流量Qk(k=1,2,…,n)，而Qk～N(μ，σ2)，那么则有[16]：

(35)

(36)

(37)

由t(n-1)分布临界值tp(n-1)知：

(38)

(39)

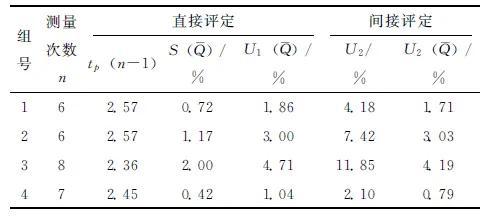
表4 两种评定结果比较

当然，不能据此就认定直接评定比间接评定更可靠。直接评定求得的平均流量标准不确定度是各测量值与平均值的分散性产生的不确定度，这种分散性是各种因素综合作用的结果。这样评定的平均流量标准不确定度属A类评定，方法简单明确，因而在实际工作中，采用直接评定方法来评定ADCP实测流量不确定度，也是一个不错的选择。

4 最大误差与测次控制指标

4.1 最大误差与标准差的关系

文献[7]在建立最大相对误差预测模型时首先考虑了最大相对误差与相对标准差的关系，并认为尚未从理论上建立起两者的关系，于是根据实测数据建立了最大相对误差与随机不确定度的经验公式。实际上，最大误差与标准差的关系从理论上早已解决[17]。

若测量值li独立且服从均值为a，标准差为σ的正态分布，即：

(40)

残差为：

(41)

则随机向量(δ1,δ2，…,δn)也服从正态分布。据此可求得最大误差max|δ|的分布函数及数字特征[17],由于：

(42)

可知:

(43)

为总体标准差σ的无偏估计。又因为：

(44)

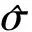
(45)

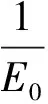
表和值表

(46)

E0与n有关。式(43)说明由系列的最大误差可直接计算出系列标准差，而且该标准差是无偏的。这就是计算标准差的最大残差法[15-17]。既然由实测流量系列的最大误差可以直接求得标准差，就没有必要再建立最大误差的预测模型了。

4.2 测次控制指标与允许误差指标

4.2.1 测次控制指标

应用流速仪法测流时，由于测流历时长，通常只能测1次就作为测流成果。为检验该成果的质量，通常在事后将实测点据点绘在水位～流量关系曲线上，观察分析该点据偏离曲线的程度，判定该次流量的取舍。如果舍去该次流量，就要在该水位节点补测1次流量。用ADCP法测流耗时短，为取得1次可靠流量成果，可以施测多次流量，然后取各次流量的平均值作为本次测流的最终成果。这里就存在一个如何判定各次流量质量，确定流量测次的问题。

美国地质调查局在ADCP流量测验质量保证规程中规定[18]：(1)在测流断面至少测4次流量，以确保有效确定流量；(2)如果4次流量的测量值中的某一个与平均值之差大于5%，应分析造成较大误差的原因，以确定是否有理由将其舍弃。如果该次流量被舍弃，应另测一次，确保有4个流量测量值，取4次流量测量值的平均值作为最终的流量值。如果找不到可以将该次测量值舍弃的理由，应再进行4次流量测验，然后将先后共8次流量测量值取平均，作为最终的流量值。

我国在声学多普勒流量测验规范中也有类似规定[13]：流量相对稳定时，应进行两个测回断面流量测量，取均值作为实测流量值。如果最大残差大于5%，属仪器安装、参数设置不当等原因引起，且不能进行有效校正的，应重新测量；如找不出确切原因，且水情平稳时，可增加一个测回。

综合上述两种规定可以看出，在用ADCP测流时，均以最大误差等于5%作为测次控制指标，当最大误差大于5%时，均要查找原因，如能找出原因，则将其舍弃并增加测次，如不能找出原因，则增加较多测次。

4.2.2 允许误差指标

文献[13]不仅规定测次控制指标，还规定了单次流量测验允许误差指标：对于一类精度水文站高、中、低水位级总随机不确定度分别控制在5%、6%、9%之内；对于二类精度水文站高、中、低水位级总随机不确定度分别控制在6%、7%、10%之内；对于三类精度水文站高、中、低水位级总随机不确定度分别控制在8%、9%、12%之内。实际上，上述允许误差指标是GB50179-93针对传统测流方法规定的。流速仪法的一份流量成果只能测一次流量，允许误差指的是单次流量。而ADCP法的一份流量成果需测n次流量，允许误差应针对n次流量的平均值。

4.2.3 两指标的协调

允许误差是控制一份流量成果的误差上限，是衡量一份流量成果质量的精度指标。测次控制指标是在测量过程合理配备测次的指标。精度指标是目的，测次控制指标为达到精度指标所采取的手段之一。因此，必须以精度指标为依据制定测次控制指标，这样才不致于使测次控制指标过宽或过严。

设ADCP法单次流量标准差由最大残差法求得，单次流量允许误差以随机不确定度UQ a表示，包含因子等于2，于是由式(43)可得：

(47)

对于一类精度水文站高、中、低水，当测次n=4时，max|δ|分别为6%、7.2%、9.6%，说明作为测次控制指标的最大误差可适当放宽，仍能使实测流量满足精度指标。反之，如果max|δ|=5%，则对于高、中、低水均有UQ a=4.2%。表面上看，似乎实测流量精度提高了，但是这与GB50179-93根据不同精度的水文站和不同水情确定不同的允许误差的宗旨是不符的，因为那种所谓的更严格的要求可能在测流实践中无法达到。

对于一类精度水文站，利用式(47)计算出不同测回允许的最大误差，见表6。

表6 一类水文站允许最大误差

5 结 论

本文提出的ADCP实测流量标准差计算模型，形式简洁，便于实用。计算结果表明，评定ADCP实测流量不确定度的间接方法和直接方法均可应用于实践中。文中建议的ADCP测次控制指标既不过于严格，又与精度指标相匹配，有利于在防汛抢测洪水中充分发挥ADCP快速出成果的作用。

[1]Simpson M R and Oltmann R N. Discharge-measurement system using an acoustic doppler current profiler with applications to large rivers and estuaries.U.S.Geological Survey, Open-File Report 91-487[R].1992:49.

[2]Simpson M R. Discharge measurements using a broad-band acoustic doppler current profiler.U.S.Geological Survey, Open-File Report 01-1[R].2001:123.

[3]刁新源，于 非，葛人峰，等.船载ADCP测量误差的因素分析和校正方法[J].海洋科学进展,2006,24(4):552-559.

[4]胡华烜,朱 敏.大倾角时的声学多普勒测速公式误差分析[J].海洋技术,2008,27(3):40-43.

[5]Terrence M J.On in situ calibration of shipboard ADCPs[J].Journal of Atmospheric and Oceanic Technology,1989,6(1):169-172.

[6]黄河宁.ADCP流量测验随机误差分析Ⅰ:随机不确定度预测模型[J].水利学报,37(5):619-624.

[7]黄河宁.ADCP流量测验随机误差分析Ⅱ:最大相对误差预测模型及现场试验验证[J].水利学报,37(6):751-757.

[8]黄河宁.ADCP流量测验原理和方法[A].田 淳,刘少华.声学多普勒测流原理及其应用[C].郑州:黄河水利出版社,2003:181-206.

[9]费业泰.误差理论与数据处理[M].北京:机械工业出版社,2007.

[10]Herschy R W. Accuracy of existing and new methods of river gauging[D].University of Reading, Reading, Berkshire, England,1975.

[11]GB 50179-1993,河流流量测验规范[S].

[12]钱学伟,陆建华.水文测验误差分析与评定[M].北京:中国水利水电出版社,2007.

[13]SL 337-2006,声学多普勒流量测验规范[S].

[14]JJF 1059-1999,测量不确定度与表示[S].

[15]刘智敏.不确定度及其实践[M].北京:中国标准出版社,2000.

[16]王中宇,刘智敏,夏新涛,等.测量误差与不确定度评定[M].北京:科学出版社,2008.

[17]刘智敏.评定精度的最大残差法[J].中国科学,1979,(4):337-344.

[18]Lipscomb S W. Quality assurance plan for discharge measurements using broadband acoustic doppler current profilers. U.S. Geological survey, Open-File Report 95-701[R].1995:7.

Uncertainty evaluation of discharge measurement by ADCP and determination of control index of number of measurements

QIAN Xue-Wei

(Hydrology Bureau of Heilongjiang Province,Harbin 150001,China)

A model for calculating standard deviation in discharge measurement by ADCP was established. Procedure of evaluating uncertainty of discharge measurement by ADCP in the indirect method was expounded and compared with results which are evaluated in the direct method.By quoting Huang He-Ning’s field test data,a case was accomplished.Based on the maximum residual method used in calculating standard deviation,the relation was analyzed between the control index of number of measurements and the precision index,and a new method for determinating control index of number of measurements of ADCP was suggested.

ADCP;discharge measurement;standed deviation;uncertainty;index of number of measurements

10.13524/j.2095-008x.2014.01.002

2014-01-03

钱学伟(1939-),男，辽宁抚顺人，教授级高级工程师，研究方向：水文监测误差分析，E-mail:qianxuewei3942@163.com。

P332.4

A

2095-008X(2014)01-0005-09