限制性Ⅲ级航道船舶阻力试验研究

俞中奇， 袁章新， 周 超

(1.湖州市港航管理局，浙江 湖州 313000； 2.上海船舶运输科学研究所 航运技术与安全国家重点实验室，上海 200135； 3.浙江省港航管理局，杭州 310009)

随着我国国民经济持续快速发展，内河船舶的运输量不断增大。为适应国民经济的发展需要，我国不断增大对内河航道基础建设的投资，建设骨干航道网，提升航道通过能力，改善通航条件。然而，内河航道建设存在土地、环境、资源等多方面制约因素，必须综合考虑土地节约、资源保护、航运安全、建设成本[1]。船舶航行阻力是影响内河航道建设与航运经济性的重要因素之一，与航道尺度关系密切，是航道设计、航道管理、船舶设计、船舶营运等部门关注的焦点。为此，浙江省港航管理局牵头，联合国内相关规划设计部门、科研院所开展了“资源节约型限制性Ⅲ级航道建设关键技术研究”工作，其中上海船舶运输科学研究所承担船舶航行模型试验。

通过限制性Ⅲ级航道船舶阻力试验研究，分析了船舶阻力变化规律，提出了1 000 t内河散货船的阻力估算公式，建立水深、航道断面对阻力影响的修正系数。

1 限制性航道船舶阻力估算方法

国内外学者通过大量的理论和试验研究，提出了许多阻力估算方法，常用的有爱尔法、兹万科夫法、施里希丁法、阿普赫金法、巴甫米尔曲线法、泰勒盖脱勒法等。对于在无限宽阔的海上航行船舶，已经形成了一套比较成熟的船舶阻力预报方法，具有较高的预报精度[2-3]。对于内河限制性航道船舶航行阻力，由于影响内河船舶航行的因素众多，船型复杂多样，阻力估算的精度总体较低。国内外学者也提出过内河船舶阻力的一些估算方法[4-8]，其中兹万科夫法应用较为广泛，但将该方法应用于计算浅水与狭水道对船舶阻力的影响等方面还有待进一步商榷[9]。因此，长期以来船模试验仍是确定船舶阻力的主要手段。

1.1 基于船模试验的阻力计算方法

船舶的总阻力主要由摩擦阻力、兴波阻力、粘压阻力等部分组成。由于粘压阻力一般所占比重不大，且难以同兴波阻力分开，故通常把粘压阻力与兴波阻力合并在一起称为剩余阻力。因此,船舶总阻力可表达成

R=RF+RR

(1)

(2)

(3)

式(1)～式(3)中：R为总阻力；RF为摩擦阻力；RR为剩余阻力；CF为摩擦阻力系数，ΔCF为粗糙度补贴系数，一般取0.4×10-3；CR为剩余阻力系数；ρ为水密度；S为船体湿表面面积。

由于采用这种方法得到的阻力计算结果与实际相当接近，因而被广泛使用。

1.2 兹万科夫公式

内河船舶阻力通常用兹万科夫公式计算。兹万科夫法是根据前苏联伏尔加河非自航驳船的试验结果，并分析其他近似公式而得出。

船舶总阻力

R=fSV1.83+ξCBAmV1.7+4Fn

(4)

(5)

式(4)～式(5)中：f为摩擦阻力系数，一般取0.17；S为船舶浸水面积(m2)；ξ为剩余阻力系数；Am为船浸水部分舯剖面面积(m2)；CB为方形系数。

兹万科夫公式可用于粗略估算一般内河自航或非自航船舶的阻力，但在限制性航道，船舶阻力受到浅水和狭水道的影响，故应用该公式时需要修正。

由兹万科夫公式中各参数的物理意义可知，该公式的前一部分为摩擦阻力,后一部分为剩余阻力。船舶在限制性航道中航行时，阻力较非限制性航道明显增大，而两者在相同船速下，其摩擦阻力相同，阻力差异主要反映在剩余阻力的增大。因此，限制性航道中的船舶阻力估算，可通过修正剩余阻力来实现。

2 船舶阻力模型试验

2.1 试验船型及航道断面参数

2.1.1 试验船型

船型参数见表1。

2.1.2 航道断面

模型试验所采用的航道断面(见图1)航道边坡斜率为1∶4，设计最低通航水位为3.2 m。试验航道参数见表2。

2.2 主要试验成果

通过对1 000 t散货船的船模阻力测量以及船模与实船的阻力换算，得到船舶在不同尺度航道中的阻力(见图2～图6)。

3 航道尺度对阻力的影响分析

3.1 水深吃水比(h/d)对阻力的影响

由图2～图5可知：船舶在航道中航行，其航行阻力随航速的增大而增大；随水深的减小而增大。

从图6可以看出，航速<8 km/h时，增大H/d对航行阻力的影响相对较小；航速>8 km/h时，增大H/d对降低航行阻力有较明显的作用。

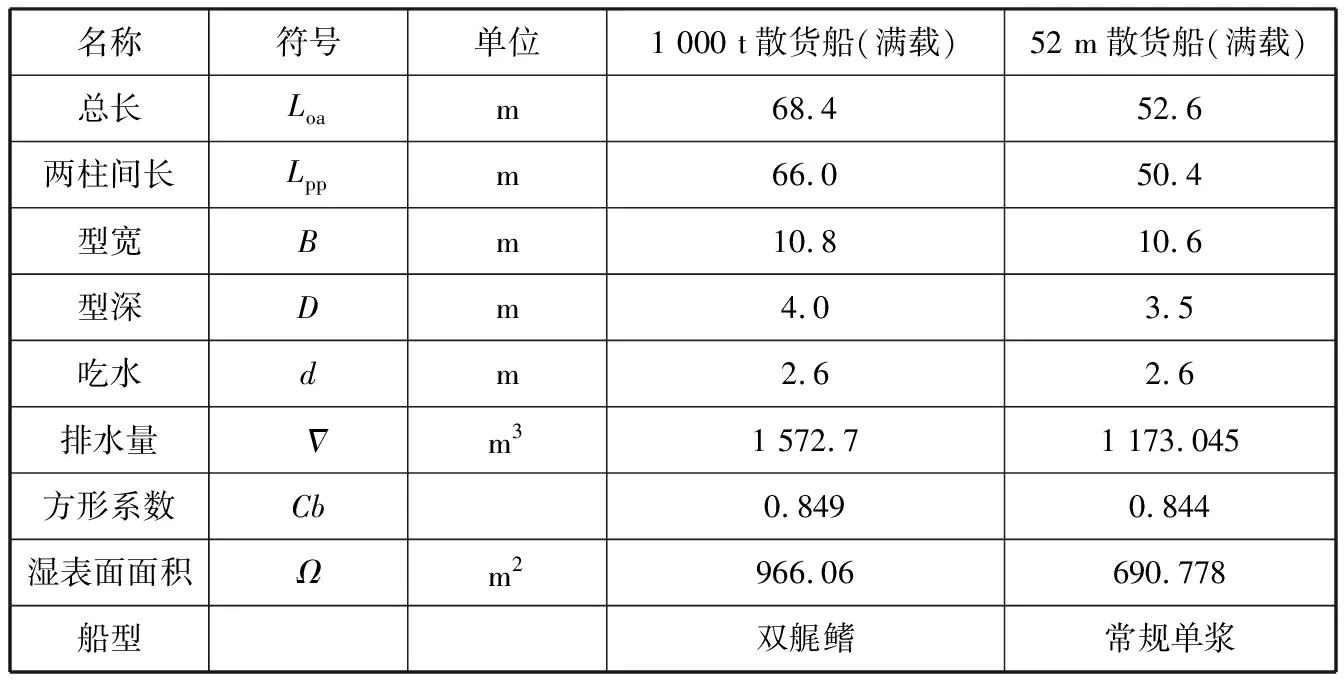
表1 1 000 t散货船船型参数

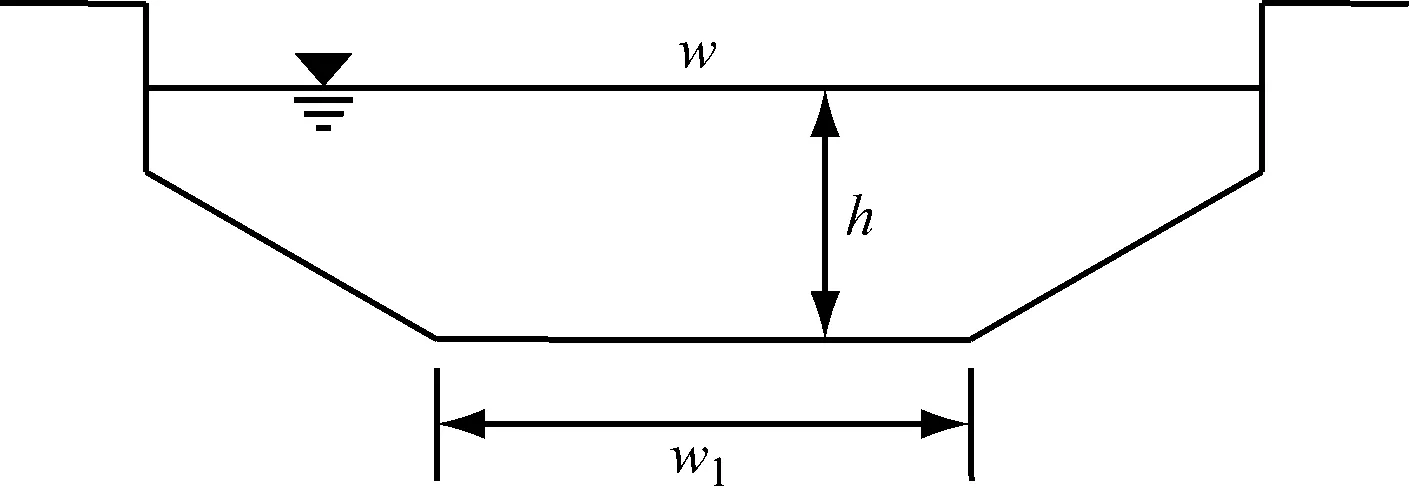
图1 试验航道断面形状

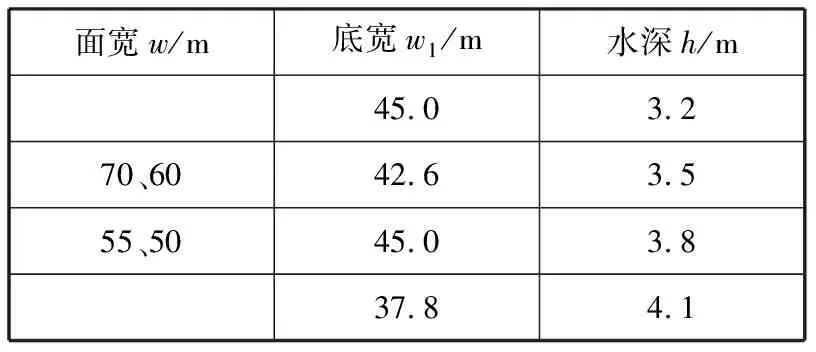
表2 试验航道参数

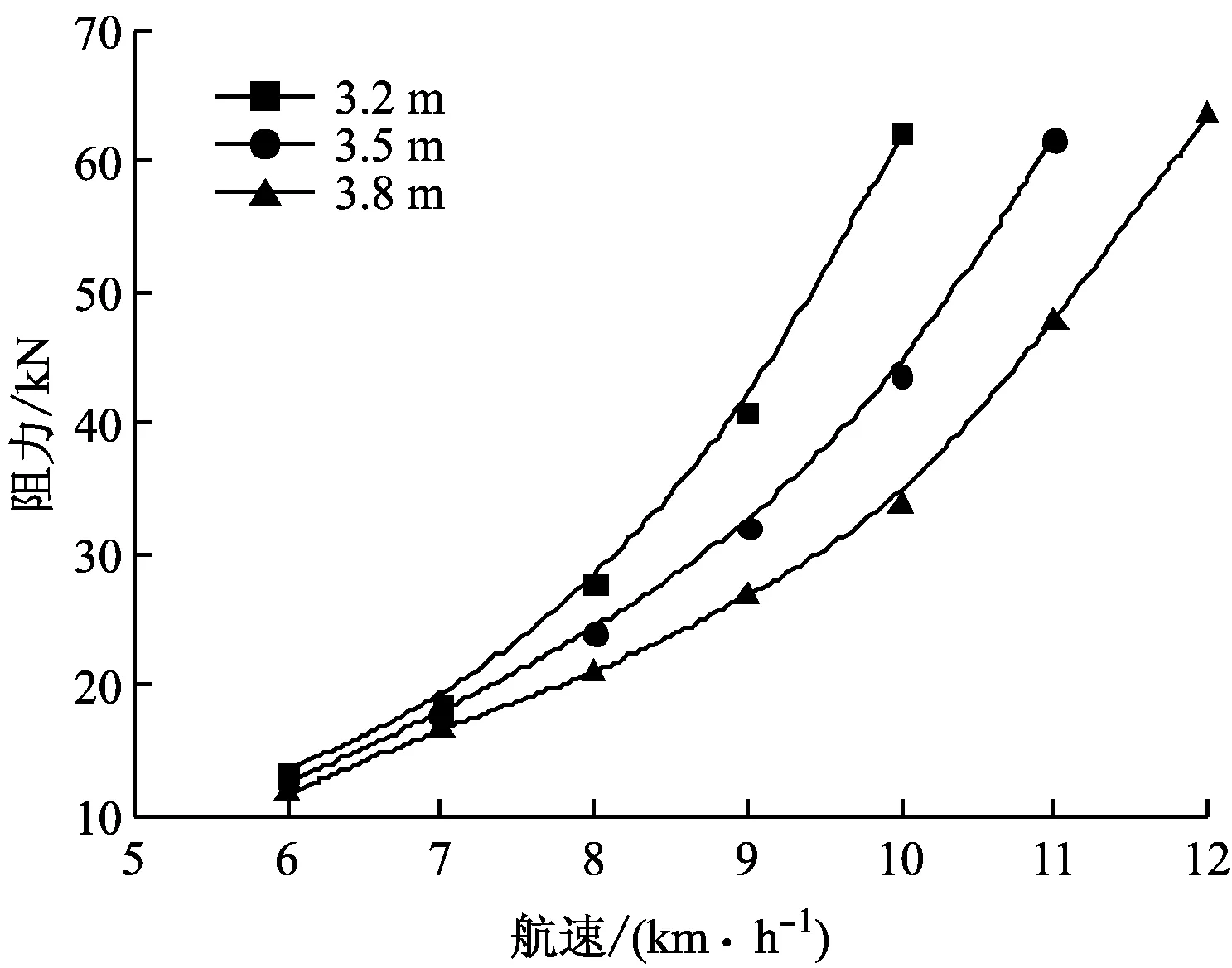
图2 50 m航道

图3 55 m航道

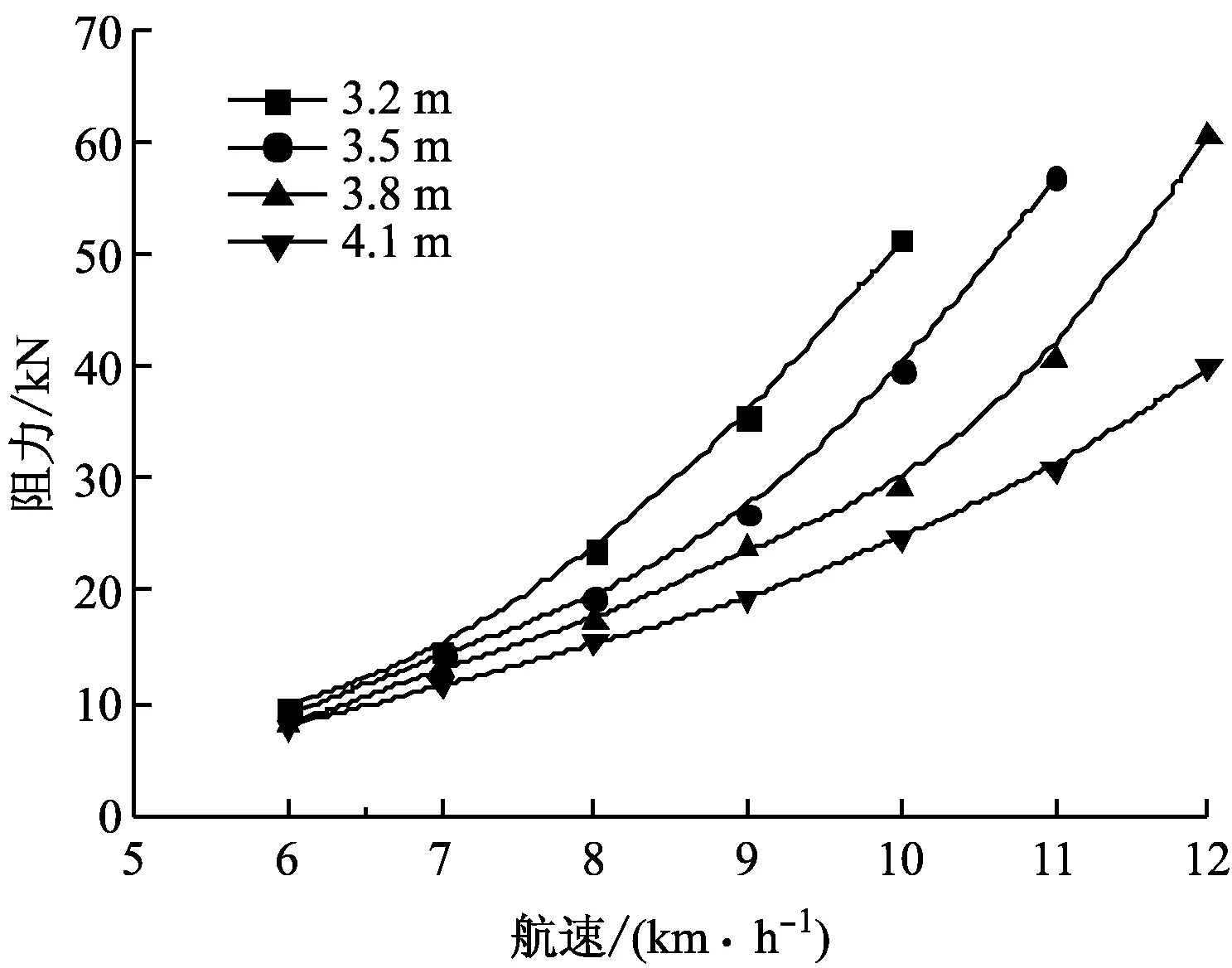
图4 60 m航道

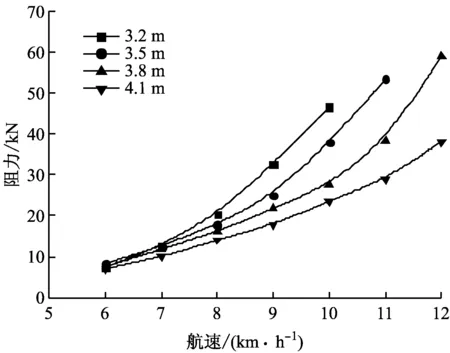
图5 70 m航道

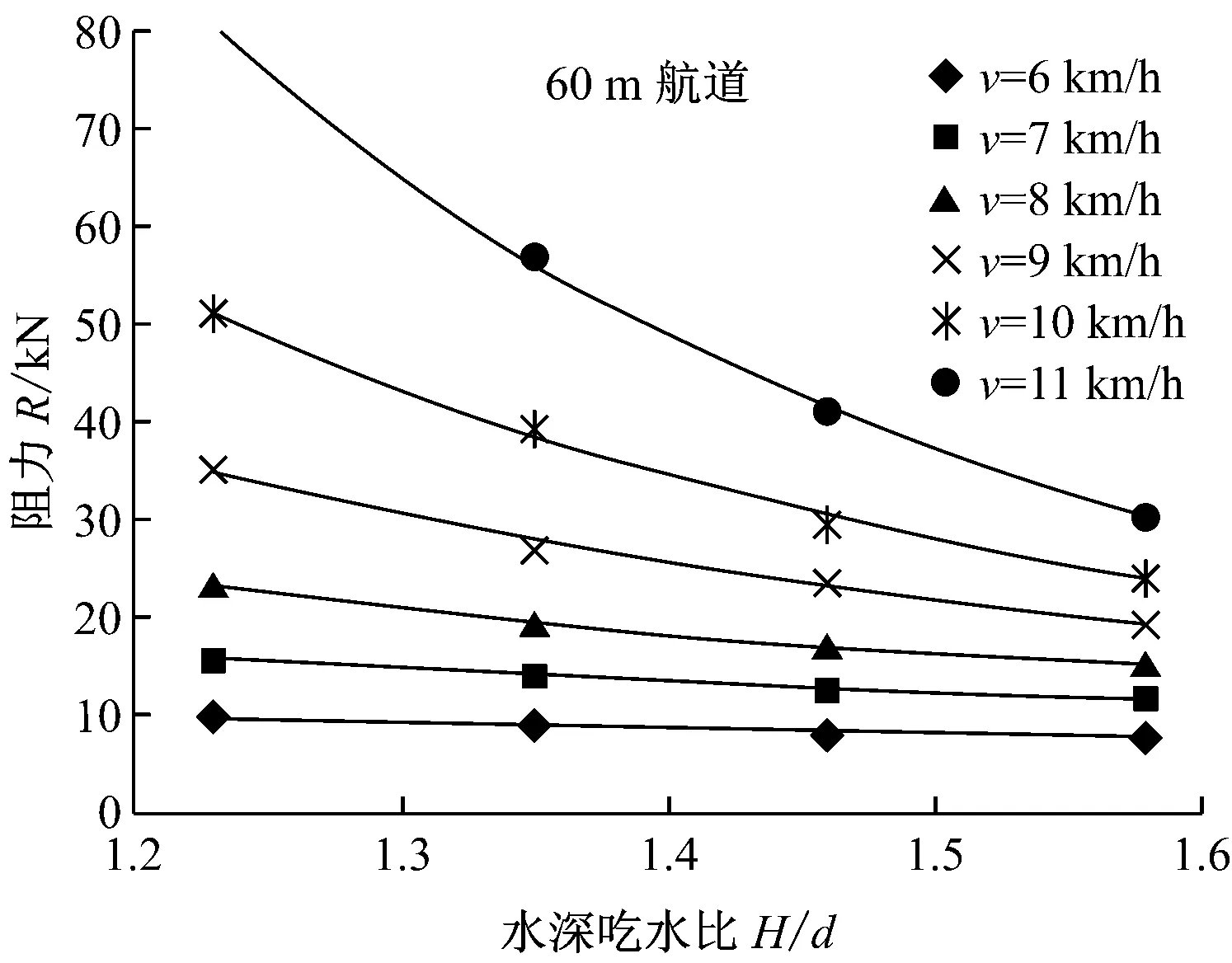
图6 阻力与h/d的关系

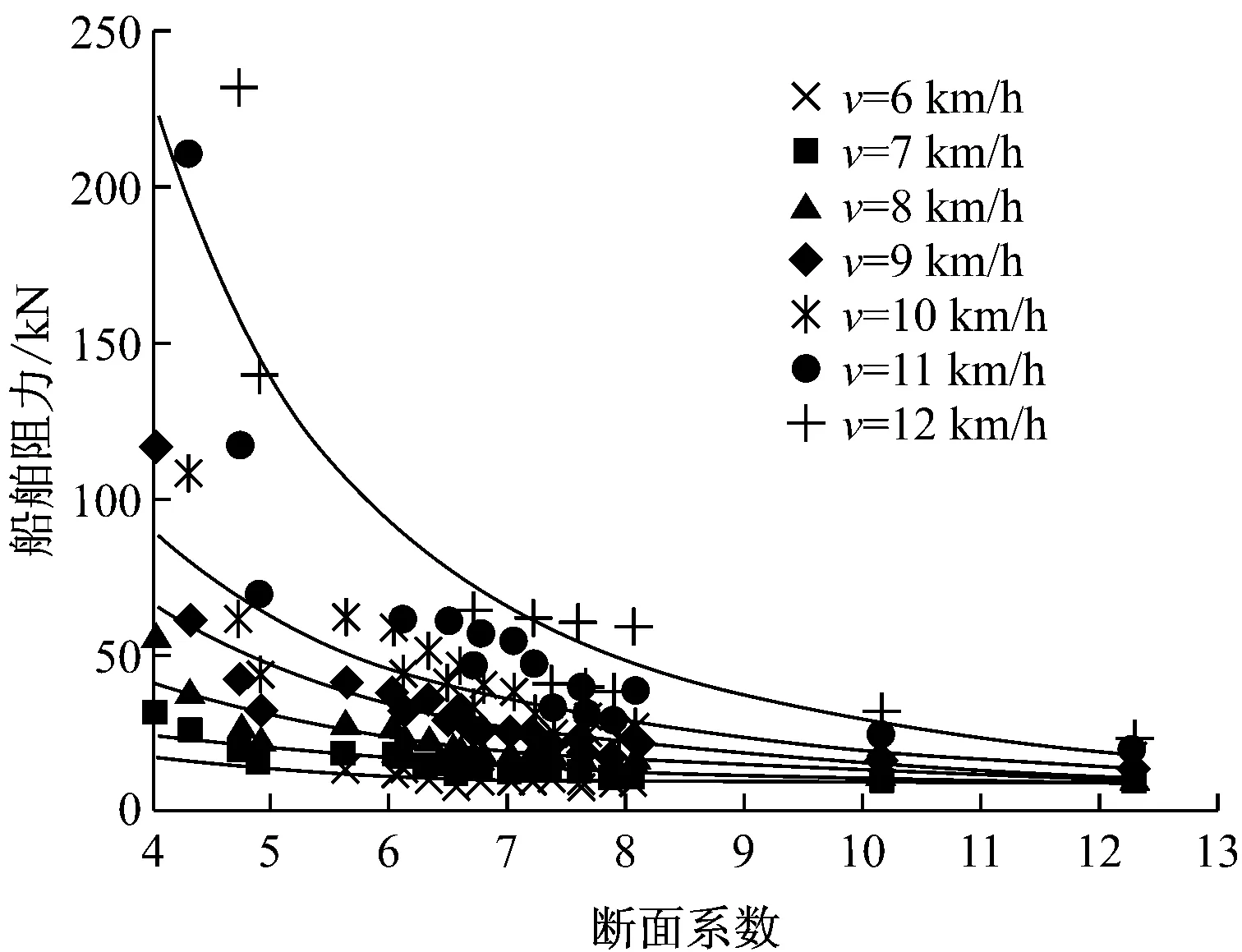
图7 阻力与断面系数n的关系

3.2 断面系数对阻力的影响

航道断面系数是影响船舶航行阻力的重要因素。试验表明，断面系数越小，船舶航行阻力越大。由图7可知，船舶低速航行时(航速<8 km/h)，断面系数<5，阻力随断面系数的减小而迅速增大；断面系数为5～8时，阻力随断面系数的增大而缓慢减小;断面系数>8时，断面系数增大，阻力变化不大。随着航速的增大(航速>8 km/h)，断面系数对阻力的影响显著增大；断面系数<6时，阻力随断面系数的减小而迅速增大；断面系数为6～10时，阻力随断面系数的增大而缓慢减小，断面系数>10时，断面系数增大，阻力变化不大。

4 限制性航道船舶阻力估算

4.1 深水中的阻力估算

应用兹万科夫公式计算了1 000 t散货船深水中的阻力，并与试验值进行了比较(见图8)。结果表明，计算值与试验值基本一致，在低速段计算值稍偏大，高速段计算值偏小，在试验的航速范围内，最大误差为8.3%。

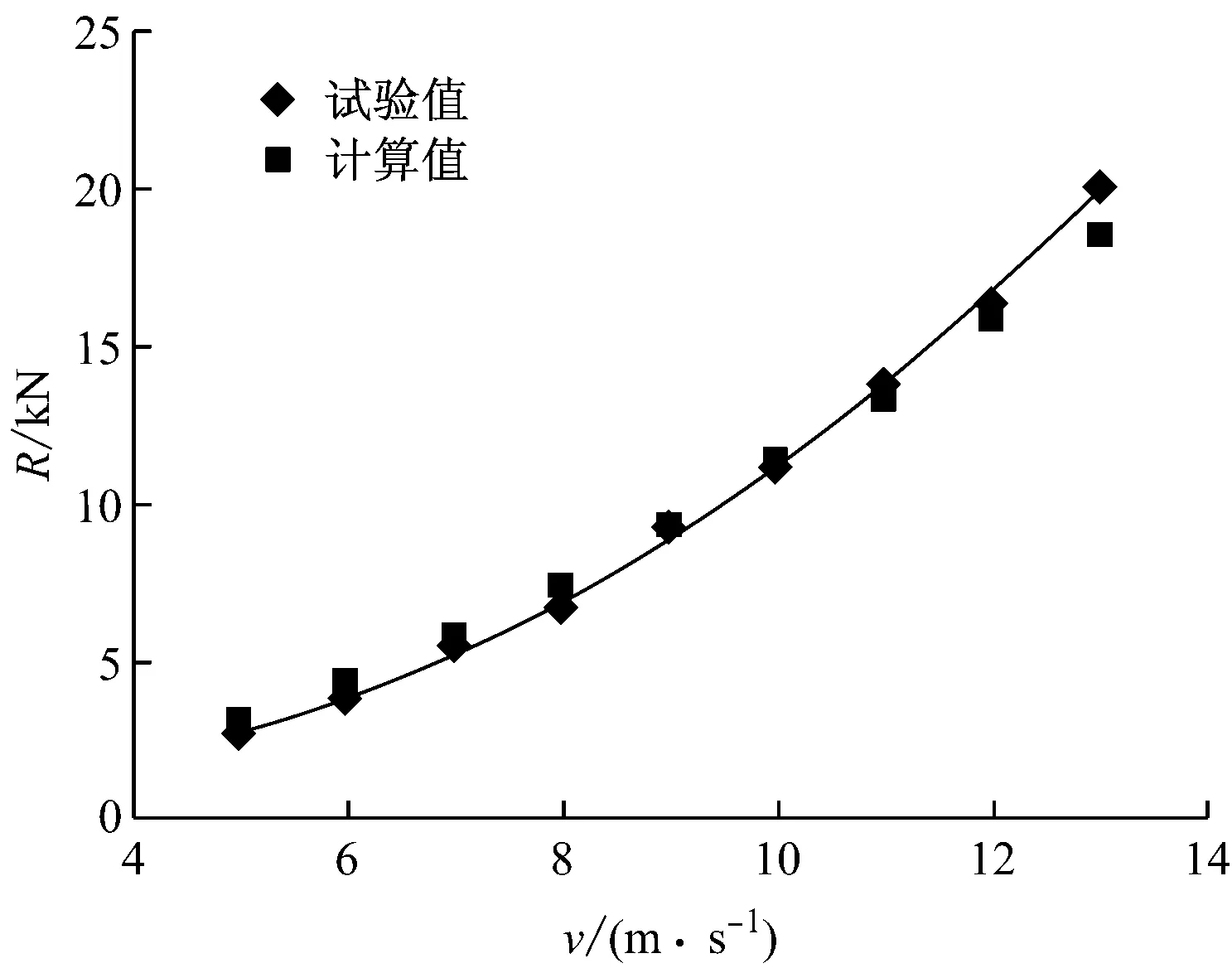
图8 深水中的阻力

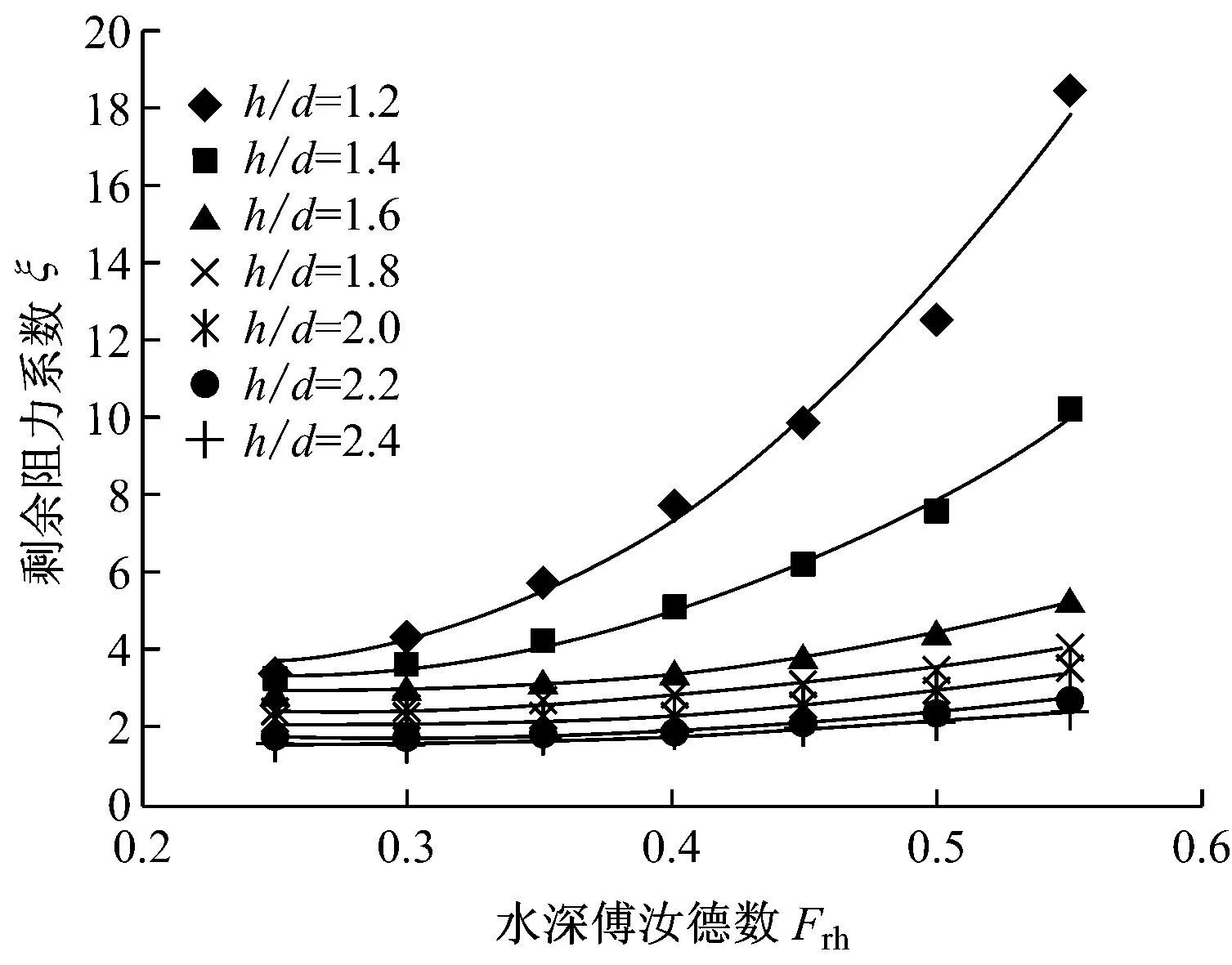
图9 剩余阻力系数与Frh的关系

4.2 限制性航道阻力估算

船舶在限制性航道中航行时，受到河道岸坡和河床底部边界的影响，船舶航行阻力比深水中大。根据相关文献，参考有关近似计算方法及公式，提出了阻力的近似估算公式。

(6)

(7)

通过对50～70 m航道的试验数据进行分析，得到剩余阻力系数ξ与Frh具有图9所示的关系。为便于计算，对剩余阻力系数进行了回归分析，得到

(8)

(9)

(10)

(11)

(12)

4.3 估算精度

为验证估算公式的精度，将试验结果与公式计算结果进行了比较，详见图10～图14(图中实线为计算值，点为试验值)，结果表明，估算具有比较满意的计算精度，平均误差≤8%。

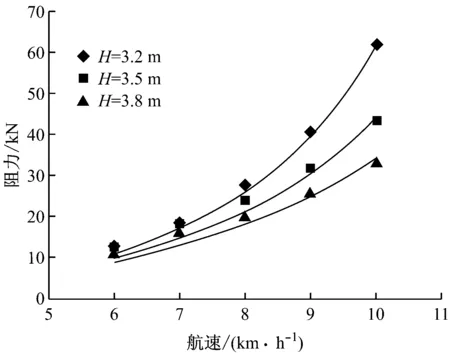
图10 50 m航道阻力比较

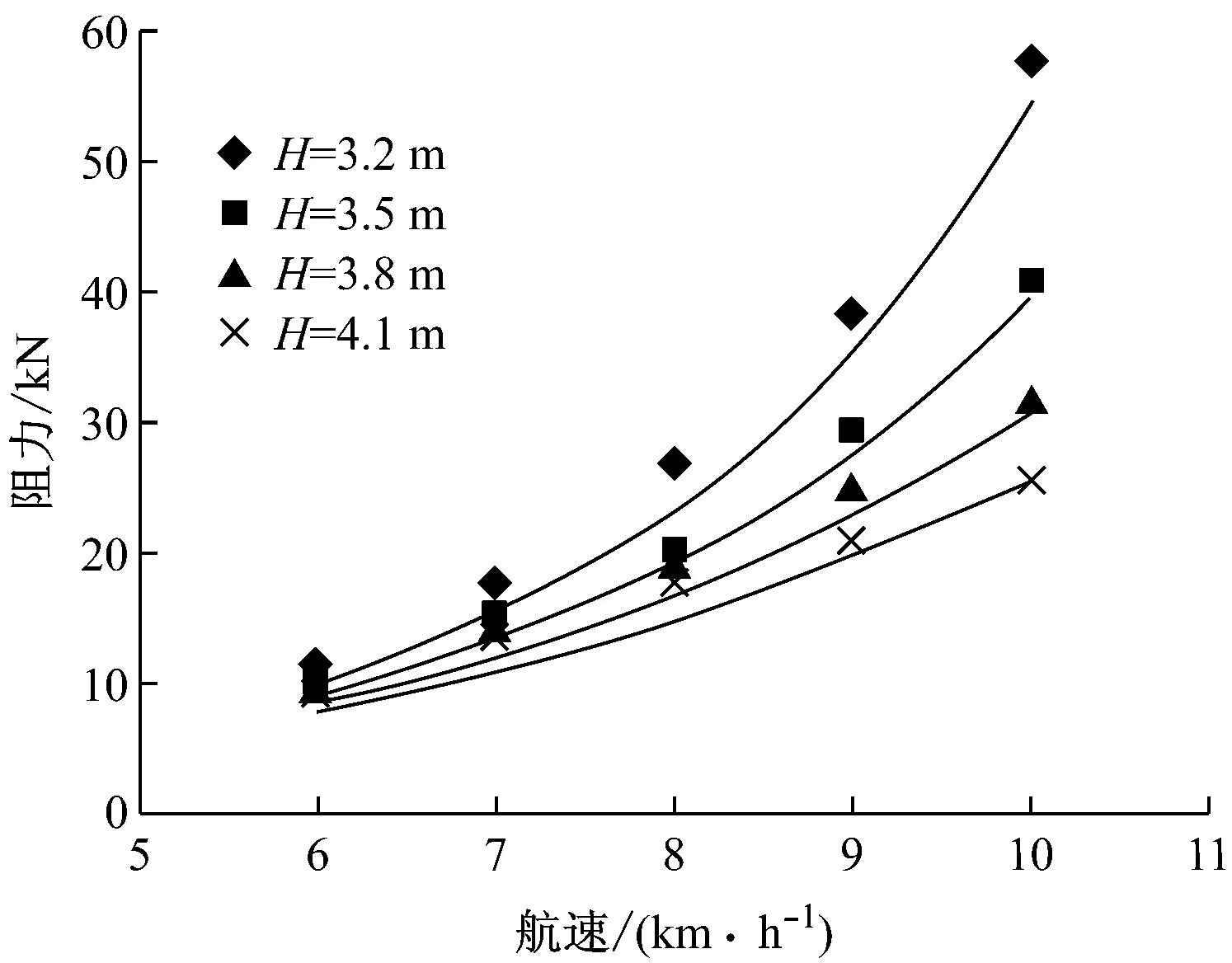
图11 55 m航道阻力比较

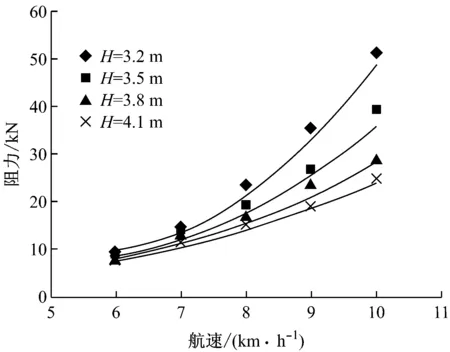
图12 60 m航道阻力比较

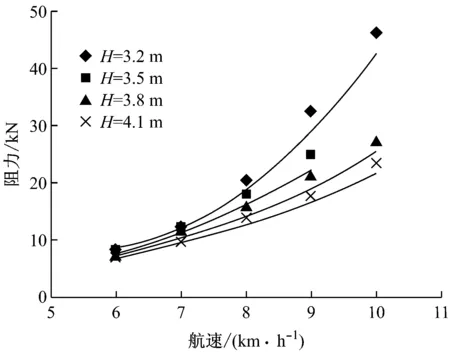
图13 70 m航道阻力比较

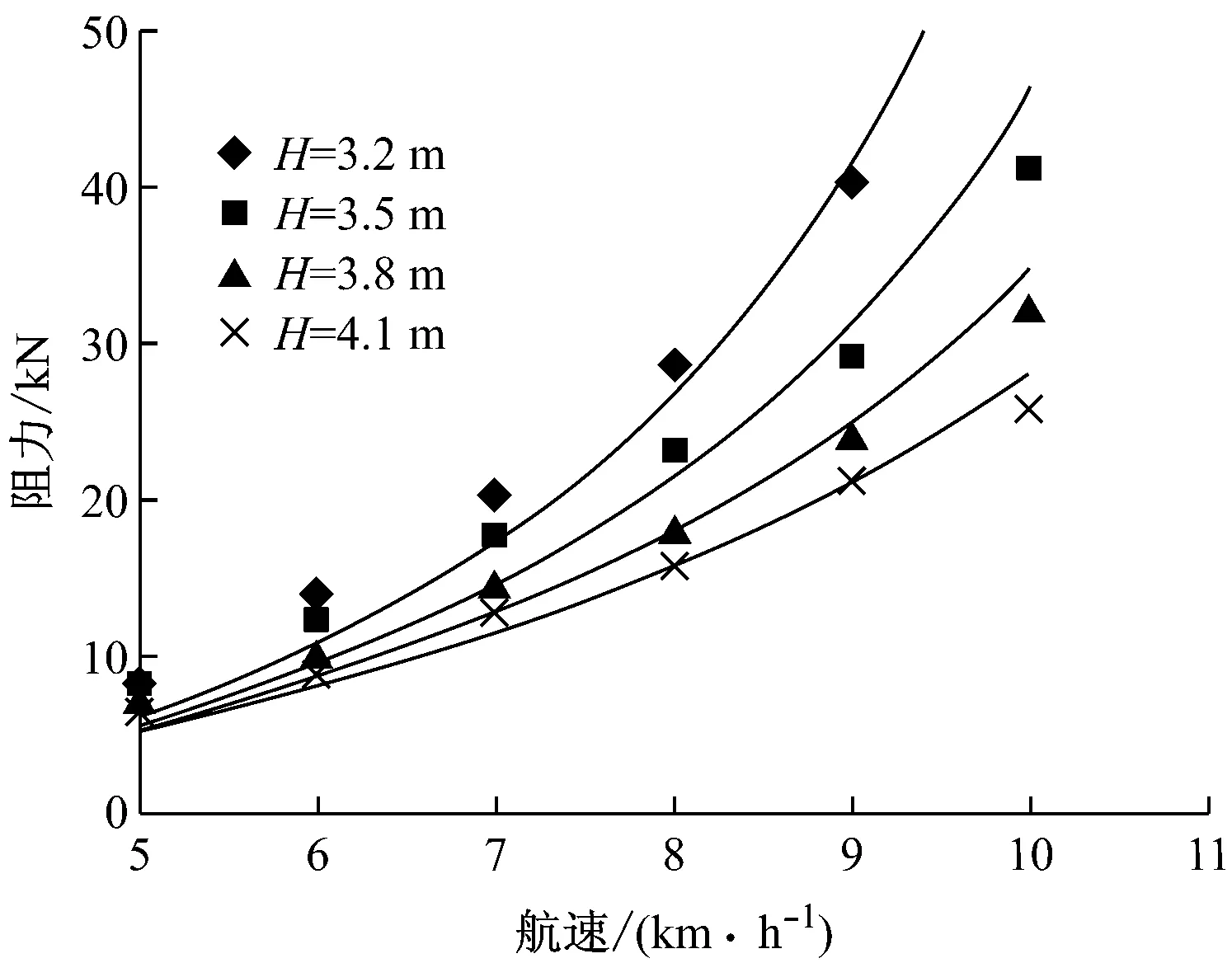
图14 60 m航道阻力比较(52.6 m船)

5 结 语

限制性航道尺度是影响船舶航行阻力的重要因素，合理的航道断面尺度不仅可以提高航道改造的经济性，而且还可以大幅降低船舶航行阻力，提高船舶航行经济性。试验表明，增大航道水深是降低船舶航行阻力最有效的措施。

应用兹万科夫公式估算内河船舶在深水中的航行阻力具有一定的精度，估算限制性航道中的阻力必须作适当修正。根据物理模型试验结果，针对具体的限制性Ⅲ级航道断面形状、面宽及水深尺度范围提出的阻力计算公式，有较高的计算精度。

由于试验的船型、船舶装载状态及航道断面有限，提出阻力估算公式适用范围仍有一定局限性，是否适用其他船型尚需要进一步研究。

参考文献：

[1] 交通运输部水运局.新理念——内河航道建设指南[M].北京:人民交通出版社,2011.

[2] Prediction of Resistance and Propulsion Power of Ships[R]. Copenhagen: Technical University of Denmark, 2010.

[3] 陈昌运，董国祥，陈霞萍，等.船舶综合性能预报系统[J].上海船舶运输科学研究所学报，2007，30(2)：81-87.

[4] 钱徐涛，张国雄.驳船阻力在不同宽度限制性航道内的阻力估算方法[C].中国造船工程学会船舶阻力性能学组论文集，1984.

[5] 沈鸿玉, 张国雄, 邵任钦, 等. 运河航道断面系数模型试验研究[R].上海船舶运输科学研究所, 1982.

[6] 钱徐涛, 张国雄, 沈鸿玉. 天然河流船舶阻力与下沉量的模型试验研究[R].上海船舶运输科学研究所,1982.

[7] Van de Kaa, E.J., Power and Speed of Push-tows in Canals[C]. Delft: Symposium on Aspects of Navigability of Constraint Waterways, Including Harbour Entrances, 1978.

[8] 李一兵.内河船舶航行阻力计算方法讨论[J].水道港口，2002，23(1)：7-11.

[9] 曹民雄,姜继红,唐存本,等. 船舶上滩阻力计算方法对比与分析[J].水利水运工程学报, 2005(2)：41-45.