CFRP中等约束钢筋混凝土方柱反复受压本构模型＊

王代玉，王震宇，乔 鑫

（1.结构工程灾变与控制教育部重点实验室（哈尔滨工业大学），黑龙江 哈尔滨 150090；2.哈尔滨工业大学 土木工程学院，黑龙江 哈尔滨 150090；3.中煤科工集团沈阳设计研究院有限公司，辽宁 沈阳 110015）

FRP约束混凝土反复受压滞回本构模型是对FRP加固混凝土构件及结构抗震性能进行研究和分析的基础.目前，国内外学者对FRP约束混凝土单调受压性能进行了许多研究，并提出了多种单调受压本构模型[1－10]，但对反复受压性能的研究却较少；而已有的研究对象多为FRP约束小尺寸的素混凝土圆柱，考虑已有纵筋和箍筋的存在对反复受压性能的研究则更少.

Shao等[11]对24个采用不同FRP材料和包裹层数约束的素混凝土圆柱进行了不同加卸载水平的反复受压试验，发现残余应变与卸载应变具有很好的线性关系，建立了FRP约束素混凝土的加卸载规则，提出了FRP素混凝土的强化型滞回本构模型.Lam和Teng等[12－13]进行了FRP约束素混凝土圆柱的反复受压试验，结果表明：加卸载历史对反复受压时的应力－应变包络线影响不大，可用单调受压应力－应变曲线代替反复受压包络线，反复加卸载可产生累积损伤，对残余应变及应力的退化有影响.并在随后的分析中建立了FRP约束混凝土圆柱的加、卸载规则，细化了再加载曲线的表述，将再加载曲线分为共同点之前的直线段和之后的曲线过渡段，建立了适于圆柱强约束的应力－应变滞回模型.王震宇等[14]对12个CFRP约束素混凝土方柱进行了反复受压试验，研究发现FRP约束方柱与约束圆柱的反复受压性能有明显差异：两者具有不同的残余应变与卸载应变关系，且再加载曲线形式也不同，圆柱近似为直线，而方柱的再加载曲线与卸载曲线相似，为下凸的曲线形式.随后基于试验结果，建立了FRP约束素混凝土方柱的滞回本构模型.Abbasnia等[15]对10个CFRP约束混凝土方柱开展了反复受压试验，建立了残余应变与卸载应变的线性关系，但并未提出相应的反复受压滞回本构模型.

针对目前FRP约束混凝土反复受压性能研究较少，且研究对象也多为小尺寸的素混凝土柱，没有考虑尺寸效应及已有钢筋对反复受压应力－应变滞回模型影响的情况，本文对较大尺寸CFRP约束钢筋混凝土方柱开展了单调及反复受压的试验研究，考察了尺寸效应、纵筋、箍筋和CFRP包裹层数对反复受压应力－应变关系的影响，在材料层面上建立了可用于CFRP约束钢筋混凝土柱非线性分析的滞回本构模型.

1 试验概况

1.1 试件设计

共设计了30个试件，根据截面尺寸分为2个系列，其中S1系列试件为12个边长305mm，高915 mm的方柱，包裹0～3层CFRP；S2系列试件为18个边长204mm，高612mm的方柱，分别包裹0～2层CFRP.未约束混凝土实测抗压强度为25.5 MPa，纵筋配筋率均为1.46%，箍筋体积配箍率分别为0，0.4%和0.8%；纵筋和箍筋分别采用HRB335和HPB235级钢筋.为保证破坏出现在柱中，上下柱端采取箍筋加密并多包裹一层CFRP.试件尺寸及配筋如图1所示，具体试件试验工况见表1.其中直径分别为6，10和12mm钢筋实测屈服强度分别为397，312和340MPa；CFRP的极限抗拉强度、弹性模量和单层厚度分别为4 340MPa，2.4×105MPa和0.167mm；MS系列碳纤维配套粘结树脂的抗拉强度及受拉弹性模量分别为46.3和2 745MPa.

图1 试件尺寸及配筋Fig.1 Dimension and reinforcement of specimens

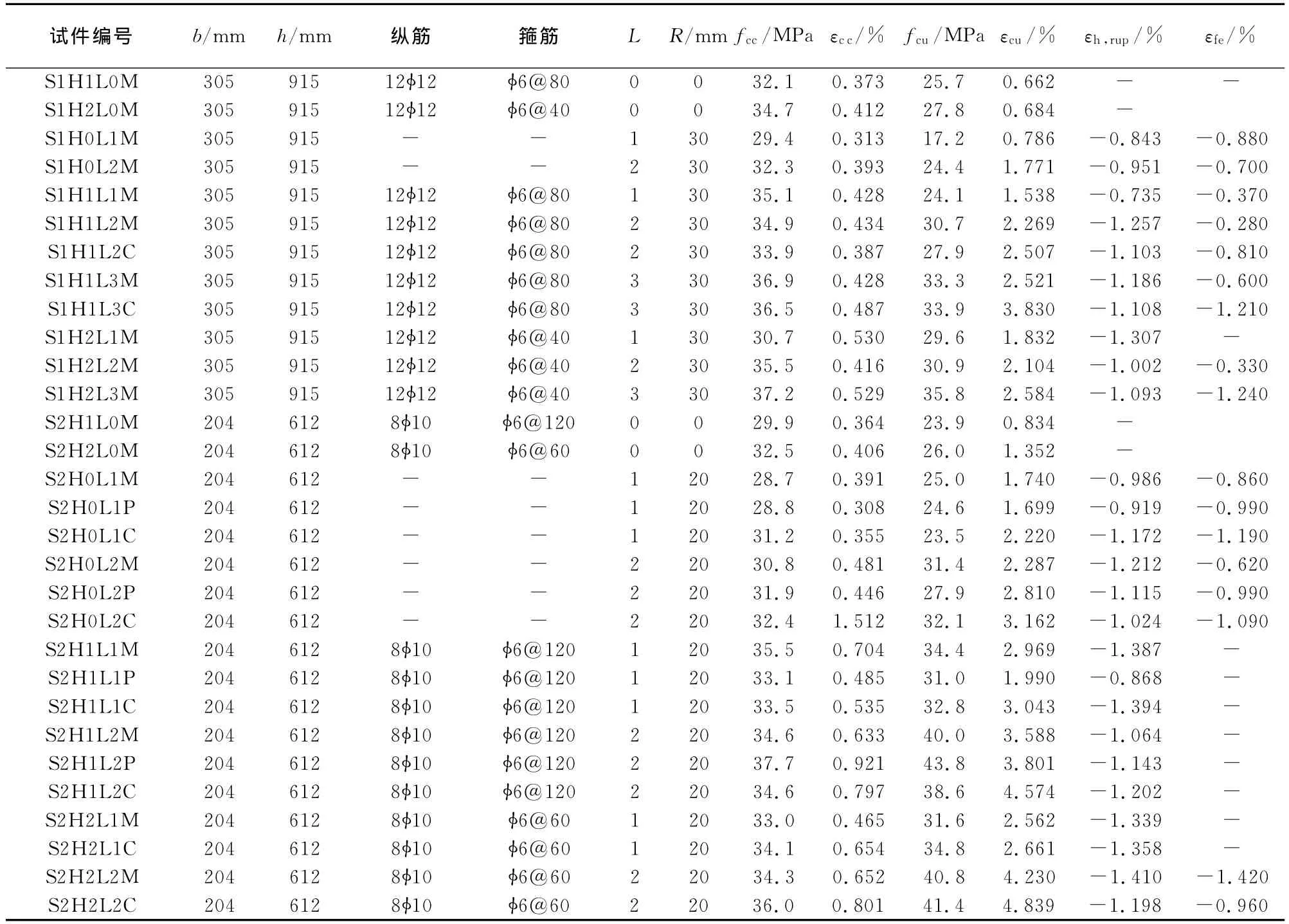
表1 试件工况及主要试验结果Tab.1 Specimen characteristics and main test results

1.2 加载及量测装置

轴向荷载采用5 000kN压力机加载，纵向位移采用4个LVDT测量，量测范围为柱中间1／3高度，箍筋和CFRP应变采用应变片量测，量测方案如图2所示.

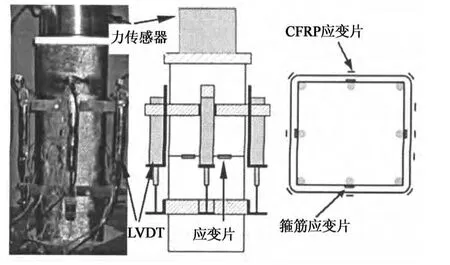
图2 LVDT及应变片位置Fig.2 Locations of LVDT and strain

2 试验结果与分析

2.1 破坏模式

试件最终破坏均是由于标距范围倒角附近区域的CFRP由于应力集中被拉断导致，典型破坏模式如图3所示.CFRP约束素混凝土试件（图3（a））破坏时表现出明显的脆性，柱中区域CFRP几乎被同时拉断，试件迅速丧失承载力.而包裹相同CFRP层数的钢筋混凝土试件（图3（b））则表现出一定的延性特征，CFRP随荷载增加而逐步拉断，直至扩展到柱中间较大区域后试件才最终丧失承载力.试验结束后剥掉CFRP发现，约束素混凝土柱（图3（c））表面出现交叉斜裂缝；而约束钢筋混凝土柱（图3（d））则表现出明显膨胀变形，箍筋由于混凝土的膨胀，受弯向外弯曲，纵筋受压屈曲成灯笼状.

图3 试件破坏模式Fig.3 Failure modes of specimens

2.2 应力－应变试验曲线

反复受压试件及对应工况下单调受压试件的应力－应变试验曲线如图4所示.图中应力为实测轴力除以试件截面面积，应变为LVDT量测位移平均值除以标距，且应力、应变均以受压为正受拉为负.由图4可知：1）与未约束钢筋混凝土试件相比，FRP约束柱的极限压应变得到显著提高，但承载力的提高幅度不大；2）应力－应变关系试验曲线多为峰值点后存在软化段的中等约束情况；3）单调受压应力－应变曲线与反复受压时的包络线整体趋势基本一致；4）对S1和S2系列柱，全部CFRP应变片量测的横向断裂应变平均值分別为CFRP极限拉应变的57%和68%，两者相差不大；而柱倒角部位CFRP应变片量测的横向断裂应变平均值分別为CFRP极限拉应变的40%和60%，由于方柱仅角部混凝土受到了FRP的有效约束，故计算FRP的有效约束作用时应取倒角部位应变片的量测结果平均值.

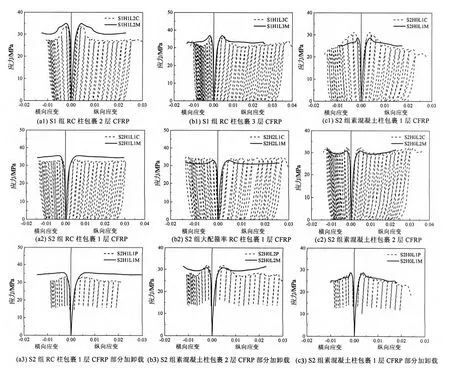
图4 应力－应变试验曲线Fig.4 Stress－strain test curves

2.3 钢筋对应力－应变曲线的影响

单调受压试验结果表明，钢筋的存在对单调受压应力－应变关系曲线形状、峰值应力及极限应变等有明显影响，详细结果讨论见文献[16－17].

本文反复受压试验结果表明：钢筋的存在对加卸载曲线同样有较大影响.部分包裹层数相同的钢筋混凝土柱和素混凝土柱反复受压应力－应变关系试验曲线的比较如图5所示.由图5可知，卸载曲线前期近似为直线，后期呈明显的曲线形式，素混凝土方柱在卸载后期的模量变化很大，而钢筋混凝土方柱的卸载模量变化较小；在卸载应变相同时，钢筋混凝土柱的残余应变明显大于素混凝土柱.素混凝土方柱与钢筋混凝土方柱的再加载曲线也不同，钢筋混凝土方柱为直线，而素混凝土方柱为曲线.因此，在建立反复受压应力－应变关系模型时不应忽略钢筋的影响.

图5 钢筋对加卸载曲线的影响Fig.5 Influence of steel bars on unloading／reloading curves

3 反复受压应力－应变模型

本文试验结果表明，由于钢筋的存在导致柱的倒角半径不能做到很大，此时对截面尺寸较大的柱其应力－应变关系曲线存在软化段，CFRP的约束作用降低，为中等约束.已有FRP约束混凝土本构模型多针对应力－应变关系曲线为单调上升的强约束情况提出，中等约束本构模型很少，考虑钢筋影响的反复受压本构模型则更少.而在实际工程中，由于构件截面尺寸较大且均为钢筋混凝土，此时约束混凝土应多为中等约束情况.故本文针对FRP中等约束钢筋混凝土方柱建立反复受压应力－应变关系模型.

3.1 有效侧向约束应力

前文试验结果表明，FRP约束钢筋混凝土柱应考虑箍筋约束对有效侧向约束应力的影响，故本文所建立的修正有效约束应力模型为：

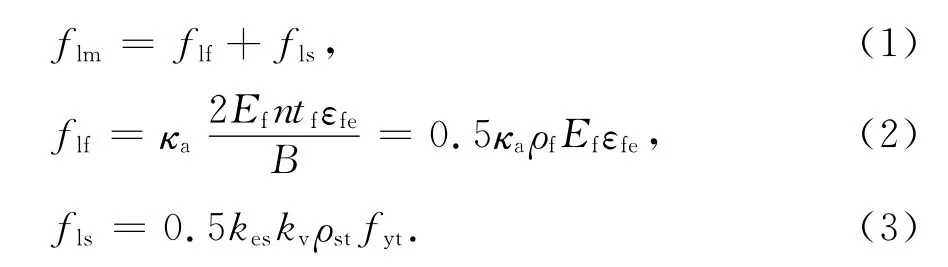
式中：flm为修正后有效侧向约束应力；flf为FRP有效侧向约束应力；fls为箍筋约束应力；Ef为FRP弹性模量；n为FRP包裹层数；tf为FRP单层厚度；ρf为FRP体积含纤率；εfe为FRP有效断裂应变，由前文可知应取倒角部位应变片量测结果平均值且应考虑截面尺寸的影响，基于试验结果本文建议：当约束方柱截面尺寸大于300mm 时，εfe＝0.4εfu，当截面尺寸小于300mm 时取εfe＝0.6εfu；ρst为体积配箍率；fyt为箍筋屈服强度；截面形状系数κa及箍筋有效约束系数kes和kv分别为：

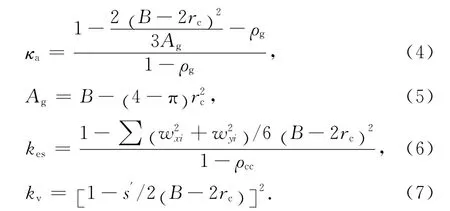
式中：ρg和ρcc分别为全截面和核心区截面纵筋配筋率；rc为截面倒角半径；wxi和wyi分别为沿截面两垂直方向第i个纵筋间净距.

目前多以FRP侧向约束应力与未约束混凝土峰值应力之比即约束比进行FRP强弱约束的界定，但已有界定标准大都未考虑钢筋及截面尺寸对侧向约束作用的影响；故本文基于建立的修正后有效侧向约束应力模型（式（1））与未约束混凝土峰值应力之比对强弱约束重新进行了界定：即当修正约束比大于0.17时为强约束，小于0.09时为弱约束，介于两者之间时为中等约束.对于FRP约束钢筋混凝土强弱约束的划分已有另文介绍，限于篇幅，本文不再重复介绍，详见文献[16－17].

3.2 包络线

本文试验及已有研究[11－12]均表明，FRP约束混凝土反复受压时的包络线可用其单调受压时的应力－应变曲线代替.故本文采用文献[16]已提出的FRP中等约束钢筋混凝土柱单调受压应力－应变模型作为反复受压时的包络线，其方程形式为：

式中：y＝fc／fcc；ycu＝fcu／fcc；x＝εc／εcc；xct＝εct／εcc；xcu＝εcu／εcc；fc，εc分别为混凝土轴向应力和应变；fcc，εcc分别为峰值点应力和应变；fcu，εcu分别为极限点应力和应变；εct为转折点应变；A＝Ec／Ep为初始上升段曲线控制参数，为混凝土初始弹性模量，fc0为素混凝土峰值应力，Ep＝fcc／εcc为约束后峰值点割线模量；α为下降段控制参数.

上式中各参数的详细计算公式在文献[16－17]中根据单调受压试验结果已经回归得到.本文基于反复受压试验结果，又对各参数进行了重新修正，修正后的极限应力和应变及下降段控制参数表达式分别为：

式中：εc0＝0.002为未约束混凝土峰值点应变.

3.3 卸载曲线

根据试验卸载曲线的形状特征，CFRP约束钢筋混凝土方柱的卸载曲线描述如下：

式中：σun和εun分别为卸载点应力和应变；εp为卸载残余应变；B0和B1为卸载曲线形状系数，由试验数据回归分析可得：

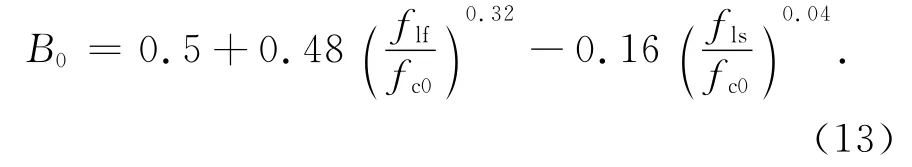
对约束钢筋混凝土柱：

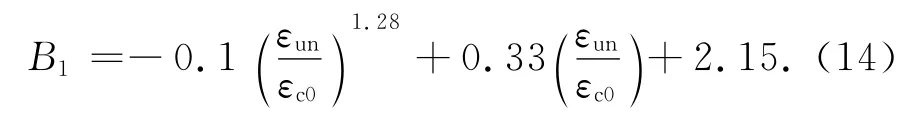
对约束素混凝土柱：

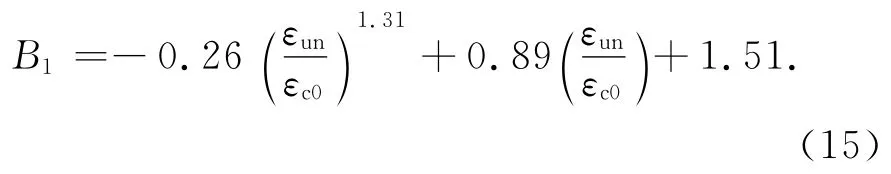
已有研究表明[11－15]，残余应变与卸载应变成线性关系，本文试验得到同样结论，但钢筋的存在对残余应变有较大影响，如图6所示.

由试验结果可知，当卸载应变小于0.001时，试件处于弹性段无残余应变产生，当卸载应变大于0.001时，回归分析得到的残余应变表达式如下.

约束钢筋混凝土柱时：

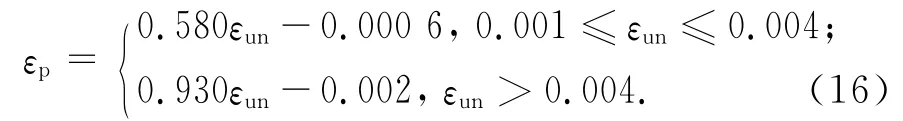
约束素混凝土柱时：

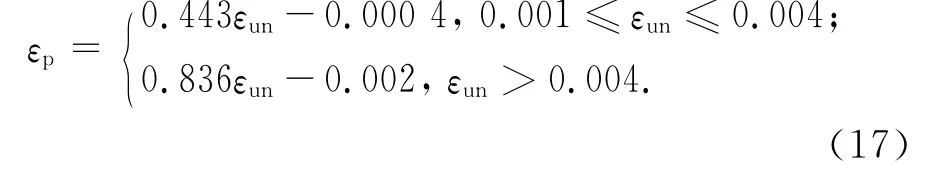
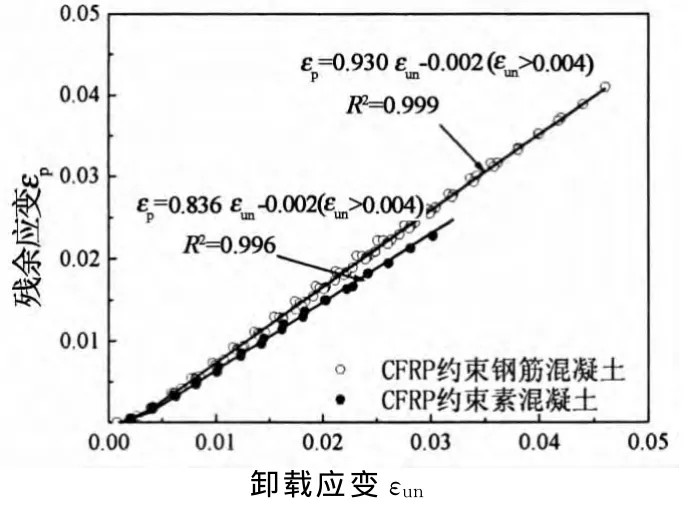
图6 残余应变和卸载应变关系Fig.6 Lastic strains versus unloading strains

3.4 再加载曲线

根据试验得到的再加载曲线特征，采用直线模型描述再加载曲线，其表达式为：

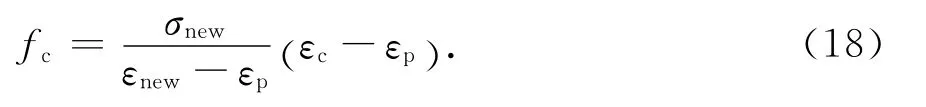
式中：σnew和εnew分别为卸载曲线与再加载曲线交点处的应力和应变，由试验结果分析可知其分别与σun和εun成线性关系，如图7和图8所示.

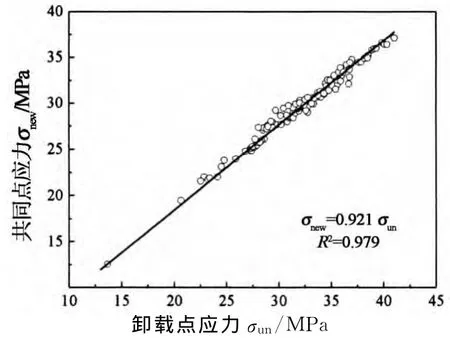
图7 共同点应力和卸载应力关系Fig.7 Stress of common points versus unload stress

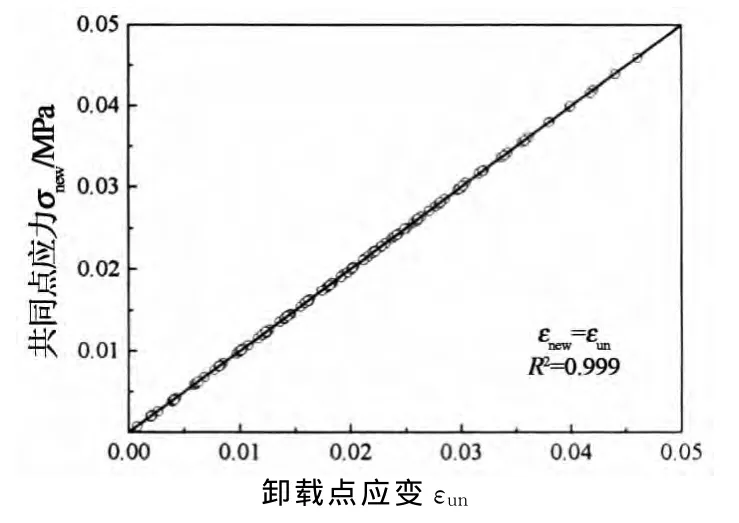
图8 共同点应变和卸载应变关系Fig.8 Strains of common points versus unload strains

基于试验数据的回归，σnew和εnew确定如下：

3.5 本文模型与试验结果的比较验证

以前述单调受压应力－应变曲线作为骨架曲线，结合加卸载曲线模型，即可建立CFRP中等约束钢筋混凝土方柱的滞回本构模型.部分卸载时先按完全卸载曲线卸载至残余应力点，然后从残余应力点以直线加载至共同点，并与骨架曲线延伸相交.部分计算结果与试验结果的比较，如图9所示.由图9可以看出，本文所提滞回本构模型对CFRP约束钢筋混凝土及素混凝土柱在完全卸载和部分卸载时均与试验结果吻合较好，模型精度较高.

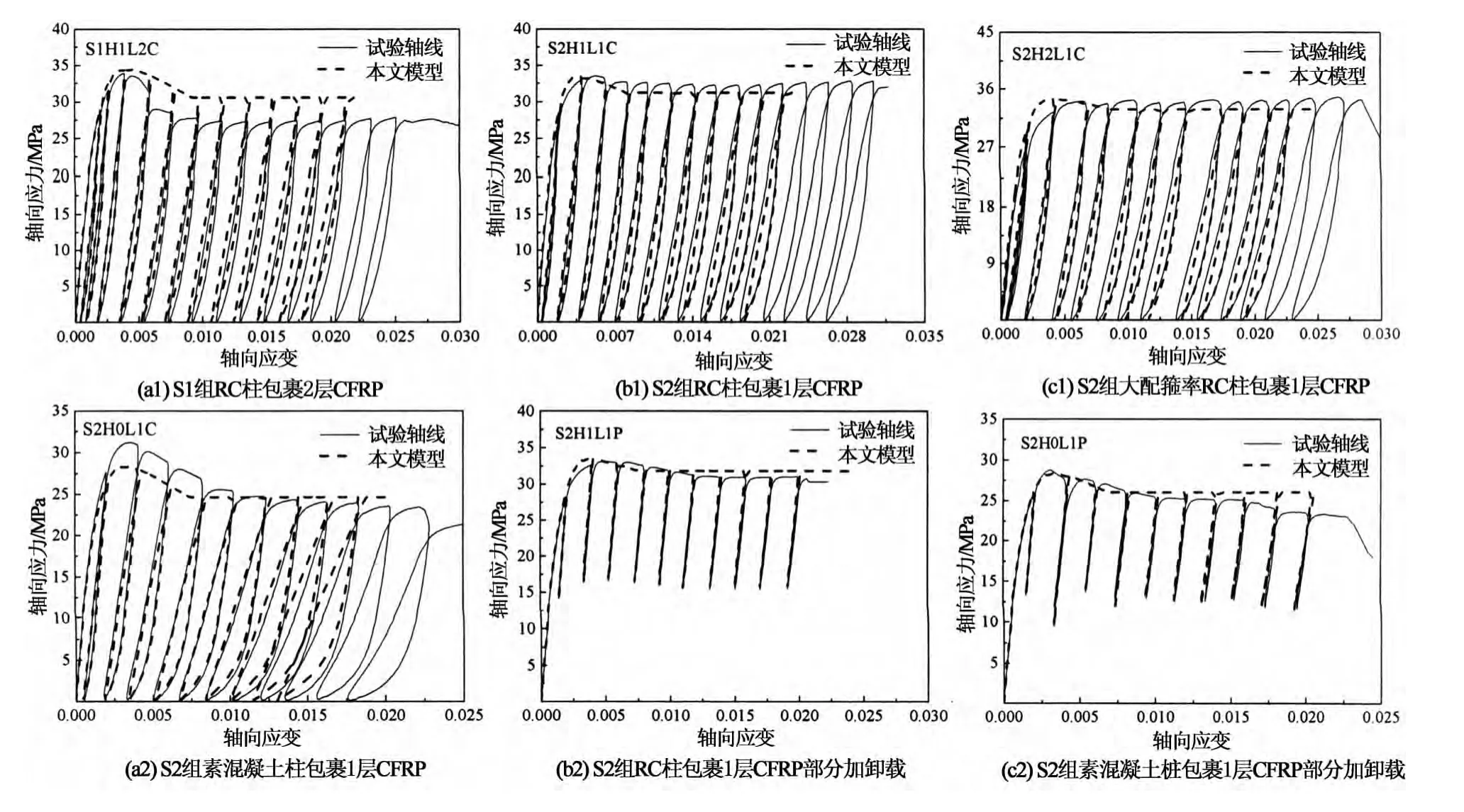
图9 计算结果与试验结果的比较Fig.9 Comparison of calculation results versus test data

4 结 论

本文对CFRP约束钢筋混凝土方柱单调及反复受压性能进行了试验研究，在此基础上建立了反复受压应力－应变滞回本构模型，得到以下主要结论：

1）对大尺寸钢筋混凝土方柱CFRP约束后明显改善了柱的延性，但对应力提高幅度不大，其应力－应变关系曲线多为峰值点后存在软化段的中等约束情况.

2）单调受压试件的应力－应变关系曲线与相同工况反复受压试件的包络线基本一致，钢筋对约束混凝土反复受压时的加卸载曲线形状及残余应变大小有明显影响，残余应变与卸载应变成很好的线性关系.

3）提出了CFRP中等约束钢筋混凝土方柱单调受压应力－应变曲线、卸载曲线和再加载曲线的数学描述，在此基础上建立了反复受压应力－应变滞回本构模型，模型预测结果与试验结果吻合较好，可用于CFRP约束钢筋混凝土结构及构件的非线性分析.

[1] XIAO Y，WU H.Compressive behavior of concrete confined by fiber composite jackets[J].Journal of Materials in Civil Engineering，2000，12（2）：139－146.

[2] ACI 440.2R－08 Guide for the design and construction of externally bonded FRP systems for strengthening concrete structures[S].MI，USA：American Concrete Institute（ACI），Farmington Hills，2008.

[3] 丁洪涛，易伟建，冼巧玲.碳纤维布（CFRP）加固压弯构件全过程分析[J].湖南大学学报：自然科学版，2003，30（3）：139－141.DING Hong－tao，YI Wei－jian，XIAN Qiao－ling.Nonlinear analysis of carbon fiber sheets（CFRP）strengthened members subjected to axial load and lateral shear[J].Journal of Hunan University：Natural Sciences，2003，30（3）：139－141.（In Chinese）

[4] JIANG T，TENG J G.Analysis－oriented stress－strain models for FRP－confined concrete[J].Engineering Structures，2007，29（11）：2968－2986.

[5] TENG J G，JIANG T，LAM L，etal.Refinement of a design－oriented stress－strain model for FRP－confined concrete[J].Journal of Composites for Construction，2009，13（4）：269－278.

[6] HARAJLI M H.Axial stress－strain relationship for FRP confined circular and rectangular concrete columns[J].Cement ＆Concrete Composites，2006，28（10）：938－948.

[7] YOUSSEF M N，FENG M Q，MOSALLAM A S.Stress－strain model for concrete confined by FRP composites[J].Composites：Part B，2007，38（5／6）：614－628.

[8] EID R，PAULTRE P.Analytical model for FRP－confined circular reinforced concrete columns[J].Journal of Composites for Construction，2008，12（5）：541－552.

[9] TURGAY T，POLAT Z，KOKSAL H O，etal.Compressive behavior of large－scale square reinforced concrete columns confined with carbon fiber reinforced polymer wraps[J].Materials and Design，2010，31（1）：357－364.

[10] 吴刚，吕志涛.FRP约束混凝土圆柱无软化段时的应力－应变关系研究[J].建筑结构学报，2003，24（5）：1－9.WU Gang，LV Zhi－tao.Study on the stress－strain relationship of FRP－confined concrete circular column without a strain－sof－tening response[J].Journal of Building Structures，2003，24（5）：1－9.（In Chinease）

[11] SHAO Y，ZHU Z，MIRMIRAN A.Cyclic modeling of FRP－confined concrete with improved ductility[J].Cement ＆ Concrete Composites，2006，28（10）：959－968.

[12] LAM L，TENG J G，CHEUNG C H，etal.FRP－confined concrete under axial cyclic compression[J].Cement ＆ Concrete Composites，2006，28（10）：949－958.

[13] LAM L，TENG J G.Stress－strain model for FRP－confined concrete under cyclic axial compression[J].Engineering Structures，2009，31（2）：308－321.

[14] 王震宇，李洪鹏.重复荷载作用下碳纤维预设混凝土加卸载准则 [J].建筑结构，2009，39（7）：100－103.WANG Zhen－yu，LI Hong－peng.Loading and unloading criteria of FRP－confined concrete under cyclic compression[J].Building Structure，2009，39（7）：100－103.（In Chinese）

[15] ABBASNIA R，ZIAADIAN H.Behavior of concrete prisms confined with FRP composites under axial cyclic compression[J].Engineering Structures，2010，32（3）：648－655.

[16] 王震宇，王代玉，吕大刚，等.CFRP中等约束钢筋混凝土方柱单轴受压应力－应变模型[J].建筑结构学报，2011，32（4）：101－109.WANG Zhen－yu，WANG Dai－yu，LV Da－gang，etal.Stressstrain model for CFRP moderately－confined reinforced concrete square columns[J].Journal of Building Structures，2011，32（4）：101－109.（In Chinese）

[17] WANG Z Y，WANG D Y，SMITH S T，etal.CFRP－confined square RC columns.I：experimental investigation[J].Journal of Composites for Construction，ASCE，2012，16（2）：150－160.