山区覆冰输电塔线体系风致不平衡张力的研究＊

杜运兴，孙 倩

（湖南大学 土木工程学院，湖南 长沙 410082）

2008年1月，在湖南、江西、浙江、湖北、贵州和云南等出现了罕见的大面积冰灾，致使电力设施承受着大大超过规范规定的荷载值，因而出现了大量倒塔断线现象，给国家电网公司带来了严重的经济损失[1].在中国北方地区，这种破坏更为常见.因而研究覆冰输电塔线体系的风致动力响应的特性是十分必要的.

为了避免覆冰对输电塔所造成的破坏，国内外许多学者对这一问题进行了大量的研究，获得了一定的科研成果.Den Hartog[2]最先发表了关于覆冰导线驰振理论研究，利用驰振理论解释覆冰后导线在风荷载激励下产生大幅振动现象.Nigol等[3－4]利用风洞实验手段，针对工程常用范围内的覆冰形状及风速研究覆冰导线风振动力响应特性.Yu等[5－6]将振动的覆冰导线用2个自由度体系模拟，分析考虑质量轴和弹性主轴中心不重合的覆冰导线驰振规律.这些研究仅针对导线覆冰后风振动力响应进行分析.Momomura等[7]通过全方位测量山区的输电塔线风致振动，得到导线气动力阻尼对整体阻尼影响作用不可忽视.李宏男等[8]对覆冰输电塔线在未考虑脉动成分的风速激励下动力响应分析，得出塔线耦联体系对覆冰导线风振有很大影响.以上研究都考虑了塔线耦合作用对整个体系风致响应的影响，但并没有注意风中脉动成分对塔线体系风致响应不可忽略的影响.李宏男[9]和陈俊旗[10]等考虑脉动风对整个体系风荷载作用下动力响应影响.

目前，针对山区覆冰输电塔线体系的风致不平衡张力缺乏深入研究，本文采用数值试验的方法模拟山区输电线路在覆冰时的风致动力响应的特性，进而研究高差对不同覆冰厚度输电塔线体系的影响.

1 有限元模型建立

为了研究相邻输电塔间的高差对覆冰输电塔线体系风致动力响应影响，本文选用山地常用的5BZBC1塔型进行研究.建立三塔四线精细三维计算模型，其中三塔依次置于同一座山的山谷、山腰、山顶，如图1所示.5B－ZBC1酒杯型输电塔几何尺寸如图2所示.计算模型采用的材料本构模型为线弹性模型，计算过程中考虑了整个体系的几何非线性.本文输电塔构件长度及几何尺寸具体参照文献[11]，水平档距为440m，导（地）线型号及物理参数如下：

1）导线型号4×LGJ—400／35，直径d＝27 mm，重量13.49N／m，弹性模量E＝6.5×1010N／m2，最大使用张力39 480N.

2）地线型号JLB40—150，直径d＝15.75mm，重量6.93N／m，弹性模量E＝1.09×1011N／m2，最大使用张力28 693N.

在计算模型中，输电塔塔身杆件用梁单元模拟.由于导（地）线具有抗扭刚度并承受一定扭矩，因而导线采用忽略剪切变形梁单元模拟，并通过定义导线的弹性模量使该单元只能承受拉力，不能受压.当应变ε＞0时，弹性模量E取导（地）线弹性模量；当应变ε＜0时，弹性模量E取为0.绝缘子串一端与输电塔横担铰接，一端与导（地）线铰接，利用刚性连接连接横担及导（地）线对应点，约束3个平动自由度来模拟，如图3所示.

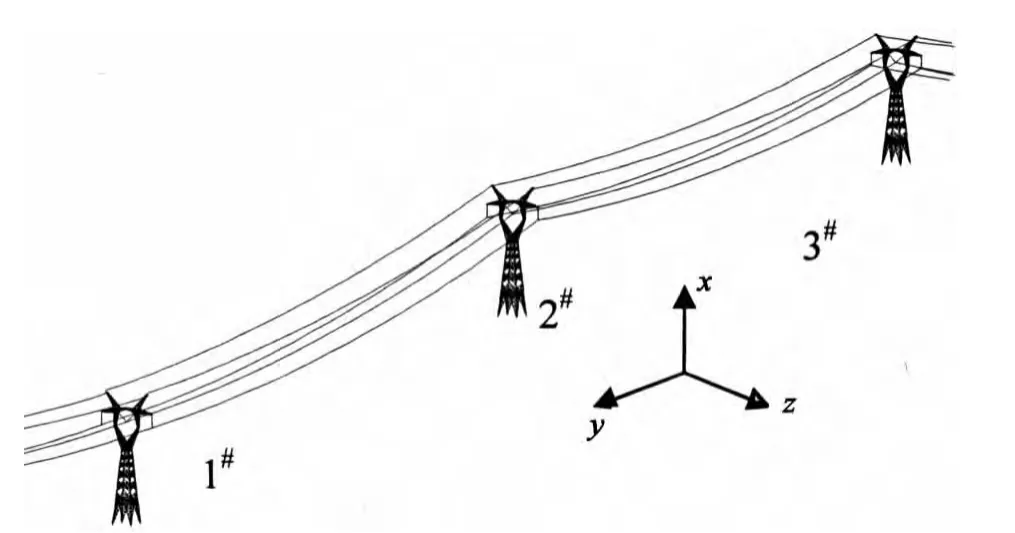
图1 输电塔线体系图Fig.1 Transmission tower－line system

图2 5B－ZBC1塔几何特性及塔身风荷载施加点分布图（单位：mm）Fig.2 Geometrical properties of 5B－ZBC1tower ＆distribution of wind load application points on tower（unit：mm）

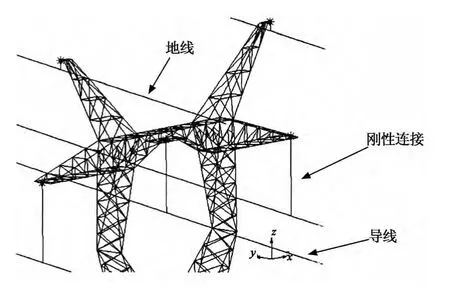
图3 绝缘子两端连接示意图Fig.3 Diagram of ends connection of insulators

1.1 杆塔及绝缘子冰荷载

根据规范[12]确定非圆截面构件每单位表面面积上覆冰荷载，按下式计算：

式中：qa为单位面积上的覆冰荷载（kN·m－2）；b为基本覆冰厚度（mm），根据当地离地10m高度处观测资料；a2为覆冰厚度高度递增系数；γ为冰重度（kN／m3）.

1.2 导（地）线冰荷载

本文不考虑覆冰对导线刚度的影响，将导（地）线冰荷载等效为导线的重力荷载，按文献[13]中公式计算：

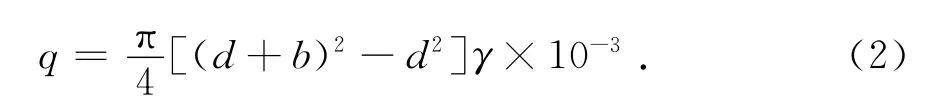
式中：q为单位长度上的覆冰荷载（N／m）；d为导线的直径（mm）；b为覆冰厚度（mm）；γ为冰重度（kN／m3），取9kN／m3.

1.3 风荷载

风速由平均风速与脉动风速组成.其中，对于平均风速沿高度变化规律，规范[14]采用指数型风剖面变化.中国规范取标准参考高度为10m，地面粗糙度指数取0.16.因而，任一高度平均风速值为：

脉动风速时程模拟的方法有：回归法、谐波合成法、逆傅立叶变换法和非均匀圆频率间隔方法[15].本文参照文献[16]，通过 MATLAB软件利用谐波合成法编写程序合成塔身荷载施加点脉动风速时程，得到t时刻施加点的脉动风速v（z，t）.

1.3.1 输电塔及绝缘子所受风荷载

本文将塔所受风载集中等效在20个施加点上，如图2所示，编号代表施加点分布情况.施加点风载可按式（4）计算：

式中：Ft为输电塔荷载施加点处风荷载值（N）；μs为构件体型系数，取2.5；As为塔承受风压投影面积计算值（mm2），取其上、下施加点间塔身受压面积各一半之和；V为风荷载施加点高度处风速（m／s）；B为覆冰时风荷载增大系数[17].

绝缘子串所受风荷载按式（5）计算：

式中：FJ为绝缘子串所受风荷载（N）；AJ为绝缘子承压投影面积（mm2）；VJ为绝缘子串中点高度处的风速（m／s）.

1.3.2 覆冰导（地）线所受风荷载

作用于覆冰导（地）线气动力荷载与作用于其他传统结构动力问题时的荷载是有区别的.它与覆于导线上冰的几何特性以及相对风攻角α非线性相关，其中覆冰导线横截面如图4所示.气动力荷载包括水平力Fx，竖直力Fz和扭矩Mθ3个分量.按文献[18]所给公式计算：

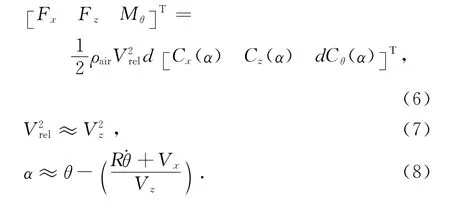
式中：ρair为空气密度（kg／m3）；Vrel为相对风速（m／s）；d为裸导线的直径（mm）；Vz为导线平均风速（m／s）；θ为初始风攻角（rad）；˙θ为风攻角角速度（rad／s）；R为导线半径（mm）；Vx为导线x方向运动的线速度（m／s）；Cx（α）为升力系数；Cz（α）为阻力系数；Cθ（α）为扭转系数.Cx（α），Cz（α）和Cθ（α）按王昕等[19]进行风洞试验的数据取值，如图5所示.本文仅针对初始风向角45°和90°两种情况进行研究.

图4 覆冰导线横截面示意图Fig.4 Transverse section of iced transmission line

图5 覆冰导线气动力系数Fig.5 Aerodynamic coefficients of iced conductors

2 模型计算

改变塔线体系中塔间高差和导（地）线覆冰厚度，风速，使塔间高差在0～105m内变化，覆冰厚度在10～30mm内变化，风速取值分别为10m／s，15m／s和30m／s.将数值模拟计算结果绘制成曲线，如图6～图12所示.其中图6～图10及图12所示结果初始风向角90°，风速30m／s.

由图6可知，2＃塔顶z方向位移随高差增加而增加，覆冰厚度越大，增长的越快.由图7和图9可以看出，在风荷载和覆冰荷载共同作用，输电塔的纵向不平衡张力随高差的增加而增加越快.规范[17]规定在山地地区悬垂塔四分裂导线情况下，塔考虑的纵向不平衡张力取值为导线最大使用张力的25%.

图6 2＃塔顶z方向位移均值Fig.6 The mean displacement in z direction at 2＃ tower’s top

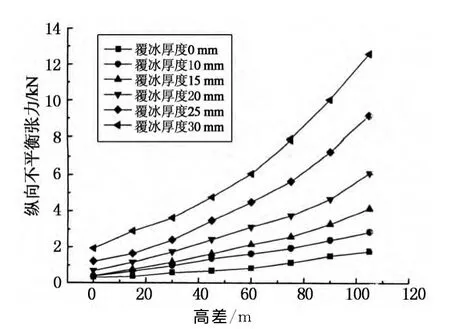
图7 2＃塔不平衡张力Fig.7 Unbalanced tension of 2＃ tower

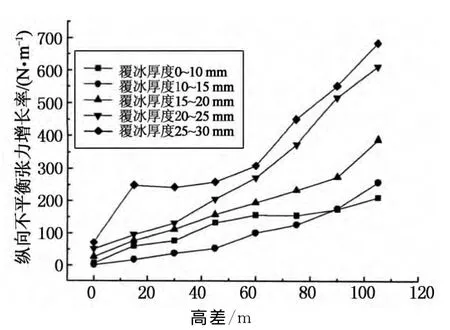
图8 2＃塔不平衡张力增长率与高差关系曲线Fig.8 Growth rate of unbalanced tension vs.elevation difference in 2＃ tower

图9 2＃塔不平衡张力Fig.9 Unbalanced tension of 2＃ tower

图10 2＃塔不平衡张力增长率与覆冰厚度关系曲线Fig.10 Growth rate of unbalanced tension vs.ice thickness curve in 2＃ tower

图11 初始风向角90°时2＃塔不平衡张力对比图Fig.11 Comparision of unbalanced tension with initial wind angle 90°in 2＃ tower

由图7可以看出，在高差105m，导线覆冰厚度30mm时，输电塔承受的不平衡张力为导线最大使用张力的31.92%.所以按规范取值设计，纵向不平衡张力取值偏小.

由图8可以看出，越大的覆冰厚度间纵向不平衡张力增长率随高差的增加趋势显得越明显.当塔间高差大于90m时，覆冰厚度0～10mm的不平衡张力增长率大于覆冰厚度10～15mm的不平衡张力增长率；当塔间高差大于60m时，覆冰厚度20～25mm的不平衡张力增长率约为覆冰厚度25～30 mm的不平衡张力增长率的1.7倍，而覆冰厚度20～25mm的增长率与25～30mm的相差不大.分析图10可知，当覆冰厚度超过20mm时，不同高差区间不平衡张力增长率相差更大；越大高差间不平衡张力增长率也越大.分析图11可知，相同覆冰厚度，在风速为10m／s较低风速下，随高差增加，不平衡张力的增加不明显；而在风速为30m／s时，随高差增加，不平衡张力的增加很明显.

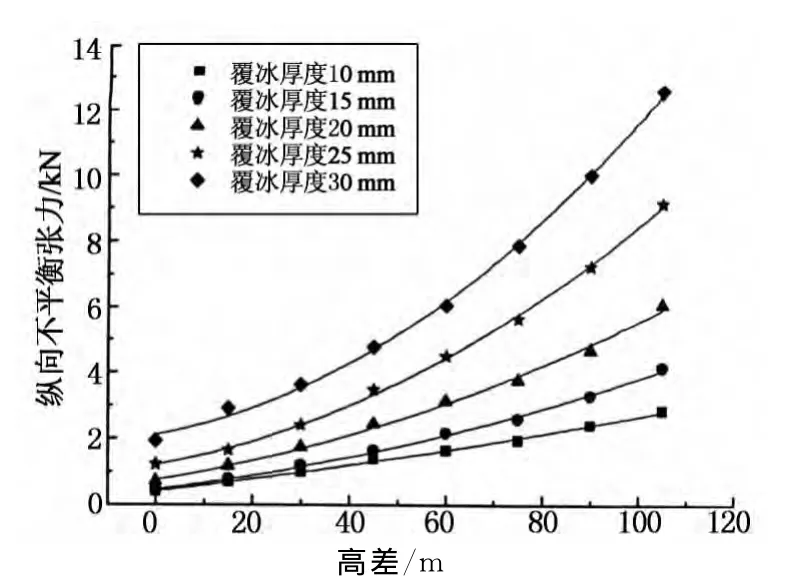
图12 2＃塔不平衡张力－高差、覆冰厚度关系曲线Fig.12 Unbalanced tension－elevation difference vs.ice thickness curve for 2＃tower

本文将输电塔的纵向不平衡张力和塔间高差、覆冰厚度的非线性关系绘制成散点图，然后进行非线性拟合.散点图及拟合曲线见图12.对以上关系拟合可以得到不平衡张力的公式为：

式中：ΔFH为输电塔纵向不平衡张力（kN）；c为塔间高差（m）；Δd为覆冰厚度（mm）；β为考虑初始风攻角和风速的影响系数，按表1取值.

表1 β取值Tab.1 Values ofβ

曲线拟合公式决定系数R2均大于0.993，平均值为0.996 74，公式拟合度很高.

3 公式验算及应用

对拟合公式（9）进行验算.验算使用的模型与拟合公式使用的模型不同，保证公式验算的意义.选取初始风向角为90°的公式计算结果与有限元结果进行对比，结果见表2.

表2 公式解与数值模拟解比较Tab.2 Comparison of solutions obtained by FEM and formula

计算结果最大误差为4.61%，最小误差为－6.65%，平均误差为－0.590 3%.由此可以看出，公式有很好的适用性.

由上节计算结果分析得到，当初始风向角90°，风速30m／s时，在覆冰厚度为30mm、高差105m时，输电塔不平衡张力按规范取值偏不安全.而在覆冰厚度不大于20mm，高差不大于105m时，按规范取值又偏于保守.

4 结 论

本文针对作用有风荷载的覆冰输电塔线体系在高差影响下不平衡张力进行了研究，得出以下结论：

1）在风荷载和覆冰荷载共同作用下，覆冰厚度越大，纵向不平衡张力随高差增长而增长的速率越大；当覆冰厚度为0和10mm时，不平衡张力随高差增长速率保持基本一致；当覆冰厚度为15mm和25mm，高差在大于60m时，纵向不平衡张力显著增加；当覆冰厚度为30mm时，纵向不平衡张力随高差保持明显增长.塔顶位移均值随高差增加而增加，覆冰厚度越大，增长越快.

2）在相同高差情况下，风荷载作用的输电塔纵向不平衡张力随覆冰厚度的增加而增加越明显.当高差为0，覆冰厚度小于15mm时，纵向不平衡张力增长平缓；当高差大于15mm时，不平衡张力增加速率随冰加厚而增加；当高差依次为30，60和90m时，纵向不平衡张力随覆冰厚度增加而增加得更显著.

3）通过大量的数值计算，在统计基础上拟合出塔线体系在风荷载作用下的纵向不平衡张力公式.该公式适用于塔型为5B－ZBC1，水平档距440m，且输电塔线路所在环境的最大风速为30m／s时的输电塔线路.利用该公式计算结果与数值模拟结果进行比较，误差在±6%以内，可以为相关设计提供参考.

[1] 李正，杨靖波，韩军科，等.2008输电塔线路冰灾倒塔原因分析[J].电网技术，2005，29（24）：16－19.LI Zheng，YANG Jing－bo，HAN Jun－ke，etal.Analysis on transmission tower toppling caused by icing disaster in 2008[J].Power System Technology，2005，29（24）：16－19.（In Chinese）

[2] DEN－HARTOG J P.Transmission line vibration due to sleet[J].AIEE Transmission，1932，51（4）：1074－1086.

[3] NIGOL O，BUCHAN P G.Conductor galloping：1.den hratog mechanism [J].IEEE Transmission on Power Apparatus System，1981，100（2）：669－707.

[4] NIGOL O，BUCHAN P G.Conductor galloping：2.den hratog mechanism [J].IEEE Transmission on Power Apparatus and System，1981，100（2）：708－720.

[5] YU P，SHAH A H，POPPLEWELL N.Inertially coupled galloping of iced conductors[J].Transmission of the ASME，1992，59（1）：140－145.

[6] YU P，POPPLEWELL N，SHAH A H.Inertially trends of inertially coupled galloping：2.periodic vibrations[J].Journal of Sound and Vibration，1995，183（4）：679－691.

[7] MOMOMURA Y，MARUKAWA H，OKAMURA T，etal.Full－scale measurements of wind－induced vibration of a transmission line system in a mountainous area[J].Wind Eng Ind Aerodyn，1997，72：241－252.

[8] 李宏男，李雪，李钢，等.覆冰输电塔－线体系风致动力响应分析[J].防灾减灾工程学报，2008（2）：127－134.LI Hong－nan，LI Xue，LI Gang，etal.Wind－induced dynamic response analysis of iced transmission tower－line system[J].Journal of Disaster Prevention and Mitigation Engineering，2008（2）：127－134.（In Chinese）

[9] 李宏男，白海峰.高压输电塔线体系抗灾研究的现状与发展趋势[J].土木工程学报，2007，40（2）：39－46.LI Hong－nan，BAI Hai－feng.State－of－the－art review on studies of disaster resistance of high－voltage transmission tower－line systems[J].China Civil Engineering Journal，2007，40（2）：39－46.（In Chinese）

[10] 陈俊旗，王伟.覆冰输电塔线体系风振响应数值模拟[J].哈尔滨工业大学学报，2011（S1）：147－151.CHEN Jun－qi，WANG Wei.Numerical simulation on wind－induced vibration oficed transmission line systems[J].Journal of Harbin Institute of Technology，2011（S1）：147－151.（In Chinese）

[11] 刘振亚.国家电网公司输变电工程典型设计－500kV输电线路分册[M].2005版.北京：中国电力出版社，2005：188－191.LIU Zhen－ya.Power transmission project typical design of State gird corporation of China－500kV transmission line branch[M].2005ed.Beijing：China Electric Power Press，2005：188－191.（In Chinese）

[12] GB 50135—2006 高耸结构设计规范[S].北京：中国计划出版社，2007：37.GB 50135—2006 Code for design of high－rising structures[S].Beijing：China Planning Press，2007：37.（In Chinese）

[13] 孟遂民，孔伟.架空输电线路设计[M].北京：中国电力出版社，2007：42－43.MENG Sui－min，KONG Wei.Overhead transmission line design[M].Beijing：China Electric Power Press，2007：42－43.（In Chinese）

[14] GB 50009—2012 建筑结构荷载规范[S].北京：中国建筑工业出版社，2012.GB 50009—2012 Load code for the design of building structures[S].Beijing：China Architecture ＆ Building Press，2012.（In Chinese）

[15] 白杰，谢强，薛松涛，等.特高压格构式输电塔线体系振动台试验设计[J].湖南大学学报：自然科学版，2013，40（4）：20－25.BAI Jie，XIE Qiang，XUE Song－tao，etal.Shaking table test model design for UHV latticed transmission tower－line coupling system [J].Journal of Hunan University：Natural Sciences，2013，40（4）：20－25.（In Chinese）

[16] 陈政清.桥梁风工程[M].北京：人民交通出版社，2005：116－119.CHEN Zheng－qing.Bridge wind engineering[M].Beijing：China Communication Press，2005：116－119.（In Chinese）

[17] GB 50545－2010 110kV～750kV架空输电线路设计规范[S].北京：中国计划出版社，2010：28－31.GB 50545－2010 Code for design of 110kV～750kV overhead transmission line[S].Beijing：China Planning Press，2010：28－31.（In Chinese）

[18] DESAI Y M，YU P，POPPLEWELL N，etal.Finite element modelling of transmission line galloping[J].Computers ＆Structures，1995，57（3）：407－420.

[19] 王昕，楼文娟，沈国辉，等.覆冰导线气动力特性风洞试验研究[J].空气动力学学报，2011（5）：573－579.WANG Xin，LOU Wen－juan，SHEN Guo－hui，etal.A wind tunnel study on aerodynamic characteristics of iced conductor[J].Acta Aerodynamica Sincica，2011（5）：73－579.（In Chinese）