预处理ICCG法求解稀疏病态方程组
于春肖,苑润浩
(燕山大学 理学院,河北 秦皇岛 066004)
许多工程、物理应用问题求解的关键是如何高效地求解大型稀疏矩阵方程组.直接解法由于在进行矩阵分解时常引入大量的填充元,导致计算过程中存储量及计算量一般很大,而且当方程组系数矩阵呈现病态时,直接解法稳定性差,致使任何中间舍入误差均可能引起最终计算结果的失真.基于上述考虑,近些年来迭代解法越来越受到重视,成为求解线性代数方程组的主要方法.可是,当系数矩阵条件数很大时,迭代法存在不收敛与收敛速度慢2个潜在问题,文献[1-2]中详细论述了预处理器的构造可使矩阵的特征值分布更集中,降低条件数.
不完全分解是一种较为通用的预处理方法,对于对称正定矩阵,可用不完全Cholesky因子分解预处理.Meijerink[3]、Van[4]及胡家赣[5]对此作了探索,指出在实际计算时,无填充的不完全分解(简记IC(0))使用最为广泛,但是这样分解的精度还不足以产生合适的收敛率.随后有不少学者就此进一步提出了相关的改进方法,如吴建平等[6]提出了带门槛不完全Cholesky改进方法、张永杰等[7]提出的大型稀疏线性方程组的改进ICCG方法.
基于此,本文提出了新的不完全Cholesky改进分解方法即在对称逐次超松弛(SSOR)预处理分解及其改进分解的基础上所产生的一类新的预处理共轭梯度法(简称SSOR-ICCG方法).
1 理论准备(ICCG法)
针对大型稀疏线性方程组大多采用迭代解法,结合适当的预处理技术,方程组良态时能够在较少的迭代次数内收敛到问题的解,并达到精度要求;方程组病态时可以很好的降低条件数,从而使方程组能够求解.不妨取线性方程组为
Ax=b,
(1)
其中A为对称正定方阵,x,b∈Rn,且x为未知向量,b为已知向量.
对系数矩阵A作不完全Cholesky分解,即A=LLT-R,其中L为下三角矩阵,R为剩余矩阵,而M=LLT为预处理矩阵.此时就得到所谓的不完全Cholesky分解共轭梯度法(ICCG).
由M=LLT≈A,可得到式(1)的等价方程组
Fy=g,
(2)
此处F=L-1AL-T,y=LTx,b=L-1b,于是具体迭代算法如下:
1)对∀x(0)∈Rn,计算r(0)=b-Ax(0),r~(0)=L-1r(0),p(0)=L-Tr~(0);
2)对于k=0,1,2,…,计算

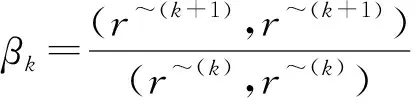
在方程组(2)中因为A对称正定,F亦然,故而M=LLT越接近于A,F就越近似于单位阵I,F的条件数就越接近最小值1,此时ICCG法的收敛速度就越快.也就是说,对于预处理矩阵M分解的好坏直接影响到对应的ICCG法收敛性的好坏.
2 一般的预处理矩阵
实际生活中采用最多的是无填充不完全Cholesky分解,简记ILLT(0)(或IC(0)),即取L的非零结构和A的下三角部分的非零结构完全一样,如下面所示:
ILLT(0)因子分解[8]
(3)
此外文献[6-7]指出,虽然上述分解保持了和A一致的稀疏性,但当矩阵A弱对角占优时,ILLT(0)因子分解的有效性会大大降低.文献[10]中给出了其修正形式,即通过适当的对角元修正策略,使预处理矩阵得以完善进而得到一种新的ICCG方法.
3 新预处理ICCG法
3.1 SSOR预处理矩阵及其改进形式
引理1[11]若矩阵A=AT∈Rn×n正定,则A=(aij)n的对角线元素均大于零,即aii>0.
引理2[11]若矩阵A∈Rn×n非奇异,则ATA为对称正定矩阵.
上述引理保证对任意非奇异方阵都可转换为对称正定阵,故假设本文所讨论的矩阵A对称正定.此外,文献[5]中胡家赣先生证明了当矩阵A对称正定时,经SSOR迭代预处理矩阵M=LLT的预处理后,矩阵F=L-1AL-T的条件数约等于系数矩阵A的条件数的平方根,从而使ICCG方法加速收敛.因此现给出以下预处理矩阵:
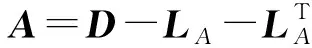
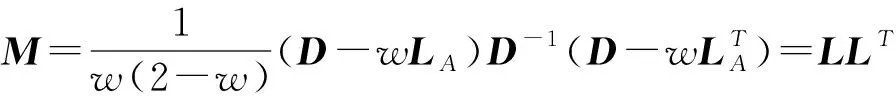
(4)
其中LA=-tril(A,-1)为A的严格下三角部分反号,D=diag(diag(A))=diag(a11,a22,…,ann)且
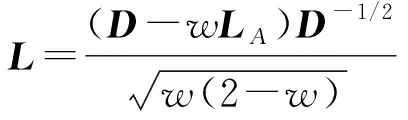
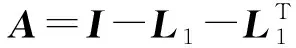

(5)
其中L1=LA+0.5(I-D),L=I-wL1.同时,指出当矩阵A的对角优势变弱时,该算法的有效性仍然保持.
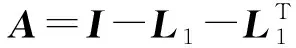
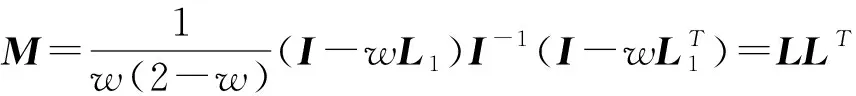
(6)
3.2 SSORICCG算法及其改进算法
算法1基于前文给出的ICCG算法,引进SSOR预处理技术,就得到了本文的SSOR-ICCG算法.具体迭代过程如下:
Step1:输入矩阵A、预处理因子w、初始值x(0)、误差精度ε1和最大迭代次数kmax,置k=0,并计算
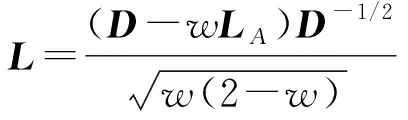
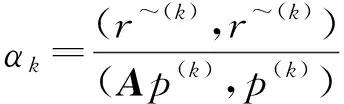
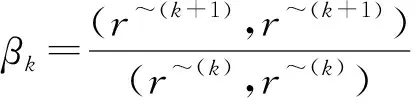
Step3:给定迭代终止条件‖x(k+1)-x(k)‖2<ε1以及k>kmax,如果满足,则算法终止,转到step4;否则转入step2继续计算;
Step4:输出数值解x(k+1)和迭代次数k.
上述过程不仅没有改变或影响ICCG算法自身的收敛性,反而经过预处理降低了矩阵A的条件数使得算法稳定性加强,收敛速度加快.
算法2若采用3)中的预处理矩阵替换算法1中的SSOR预处理矩阵,就得到了SSOR-ICCG改进算法.由于其迭代过程和算法1相似,故只需将对应的矩阵L替换即可,此处就不再赘述.
为了说明上述算法的收敛性,给出如下定理:
定理[8]设A为一对称正定矩阵且A有近似分解式M=LLT≈A,取F=L-1AL-T,则求解方程组(2)时,对于任意给定的初值x(0),预处理ICCG方法收敛且有以下误差估计式
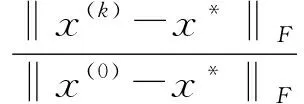
(7)
4 数值算例与分析
为验证上面理论分析、说明新预处理ICCG算法的有效可行性,进行了如下数值模拟仿真实验,并且数值实验结果表明新预处理ICCG法是比较合理有效的.
文中采用相同的迭代终止条件‖x(k+1)-x(k)‖2<10-6和k≤3 000,符号k表示迭代次数,‖ε*(x)‖2表示相对误差,w表示预处理松弛因子(其中文献[9]算法w=1.2,本文算法1,2中w=0.85).
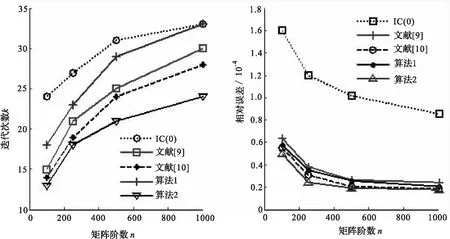
算例1:所考查的大型稀疏线性方程组为单位正方形区域Ω={(x,y)|0 为更直观的说明文中算法的优劣性,针对数值模拟仿真实验所得数据可从迭代次数和相对误差2方面给出计算结果分析,如下图1、图2所示. 此处须说明:1) 图1、图2中实际网格内点数n为图示中的平方数.2) 上述数值计算及绘图都是在Intel(R) Core(TM) i3CPU型号的微机上用Matlab 2010b实现的,并且随着CPU和Matlab版本不同,数据会略有变动. 图1 不同阶数下算法收敛速度比较 图2 不同阶数下算法求解精度比较 Fig.1 Algorithm convergence speed comparison Fig.2 Algorithm accuracy comparison under under different order number different order number 由图1、图2易得:本文算法(即新预处理ICCG法)对求解大型稀疏线性方程组是可行的,且比一般的无填充不完全ICCG法(即IC(0)法)有效;此外在相同的网格划分下,算法1与文献[9-10]中Evans和张永杰给出的有效方法相比,求解精度相差无几具有一定的可行性;其改进算法2相对上述算法可在较少的迭代次数下求得高精度的数值解,而且网格划分越细其求解的有效性、优越性愈明显. 算例2:考查大型病态线性方程组,系数矩阵为经典病态阵Hilbert矩阵,此时方程组为 Hx=b, 易得,上述方程的精确解为x*=(1,1,…,1)T,不妨取迭代初值x(0)=(0,0,…,0)T. 同样的根据数值仿真实验所得数据,可从迭代次数和相对误差2方面给出计算结果分析,如图3、图4所示. 图3 不同阶数下算法收敛速度比较 图4 不同阶数下算法求解精度比较 Fig.3 Algorithm convergence speed comparison Fig.4 Algorithm accuracy comparison under under different order number different order number 由上面的图示可以得出以下结论: 1)本文算法对求解大型病态线性方程组很有效,且算法2较算法1更优越; 2)算法1较文献[9-10]解法,迭代次数略多但求解精度方面却相差无几,具有一定的可行性; 3)算法2与上述各种算法相比,可以通过较少次数迭代求得较高精度的数值解,且矩阵阶数越大,方程组越病态其求解有效性越突出. 文中探讨了SSOR预处理分解及其改进分解,并基于此种分解分别给出了对应的预处理矩阵M和新预处理ICCG法,而后从理论角度说明了算法收敛性.最后,通过数值仿真实验进一步证实本文算法确实具有很高的可行性和实用价值. 参 考 文 献: [1] MANTEUFFEL T A. An incomplete factorization technique for positive definite linesr systems[J]. Math Comp, 1980, 34:473-497. [2] BEAUMENS ROBERT. Iterative solution methods[J]. Applied Numerical Mathematics, 2004,51(6):437-450. [3] MEIJERINK J A , H A VAN DER VORST. An iterative solution method for linear systems of which the coefficient matrix is a symmetric M-matrix[J]. Mathematics of Compytation, 1977, 31(137): 148-162. [4] HENK A,VAN DER VORST, KEES DEKKER. Conjugate gradient type methods and preconditioning[J]. J Comput Appl Math, 1988, 24(1-2): 73-87. [5] 胡家赣.线性代数方程组的迭代解法[M].北京:科学出版社,1999. [6] 吴建平,王正华.带门槛不完全Cholesky分解存在的问题与改进[J].数值计算与计算机应用,2003,3:208-210. WU Jianping, WANG Zhenghua. Problems and improvements to the incomplete cholesky decomposition with thresholds[J]. Journal of Numerical Methods and Computer Applications, 2003, 3: 208-210. [7] 张永杰,孙秦,李江海.大型稀疏线性方程组的改进ICCG方法[J].计算物理,2007,24(5):582-583. ZHANG Yongjie, SUN Qin, LI Jianghai. An improved ICCG method for large scale sparse linear equations [J]. Chinese Journal of Computational Physics, 2007, 24(5): 582-583. [8] 《现代应用数学手册》编委会编. 计算与数值分析卷[M].北京: 清华大学出版社, 2005. [9] EVANS D J. The analysis and application of sparse matrix algorithms in the finite element method[J]. J Inst Math Appl,1973, 9: 427-446. [10] 张永杰,孙秦.大型稀疏线性方程组新的ICCG方法[J].数值计算与计算机应用,2007,28(2):135-136. ZHANG Yongjie, SUN Qin. A new ICCG method of large scale sparse linear equations[J]. Journal on Numerical Methods and Computer Applications, 2007, 28(2): 135-136. [11] 蔡大用,白峰杉.高等数值分析[M].北京:清华大学出版社,2000.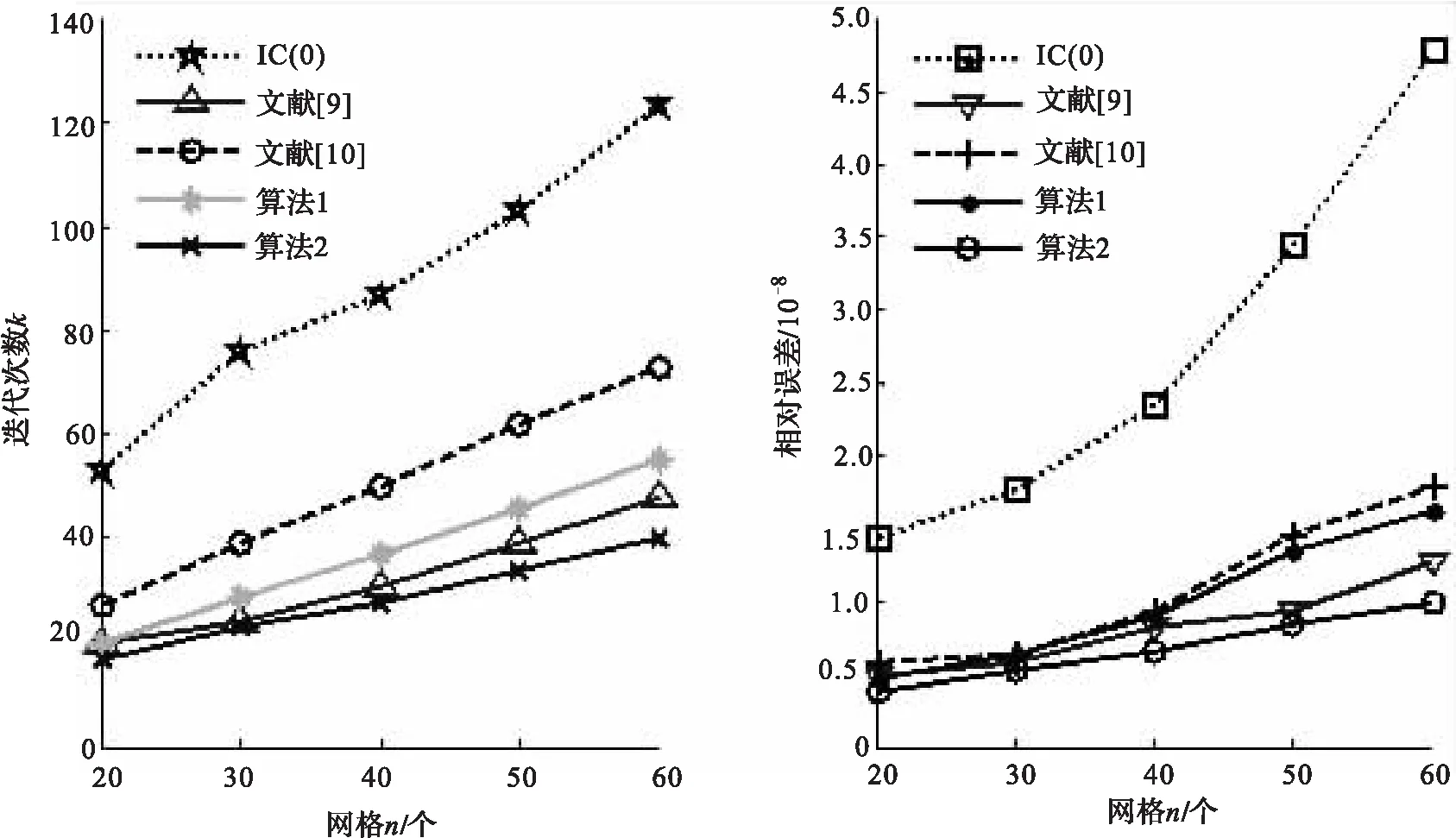
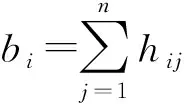
5 结束语

