一种迭代求解特征值的定姿方法
刘晓辉, 党亚民,王潜心
(中国测绘科学研究院,北京 100830)
一、引 言
(1)

F.L.Markley提出,一种利用奇异值分解(UVD)求解最优姿态矩阵Aopt的方法[6-7];Davenport把二次罚函数转换成四元数形式[3],这是对Wahba问题的极大简化,因为求解最优四元数比求解有9个元素的最优姿态矩阵所受约束更少;Keat详细说明了如何通过计算特征值和特征向量来求解最优四元数[8]。但是对矩阵进行奇异值分解,或直接求解矩阵特征值和特征向量对计算机要求较高,因此本文提出一种最优化的直接计算的方法。
二、最优化定姿方法
1. 基于奇异值分解(UVD)的最优化定姿方法[6-7]
定义函数g(A)如下
(2)

当g(A)取最大值时,L(A)最小,因而问题转化为求得使g(A)最大的Aopt,对B进行奇异值分解,可以得到
B=USVT
(3)
令
d=det(U)det(V)
(4)
则
Aopt=U[diag(1,1,d)]VT
(5)
2. 计算矩阵所有特征值和特征向量的最优化方法
Davenport[3]把姿态矩阵A转化为四元数[9]形式,四元数定义式为
(6)
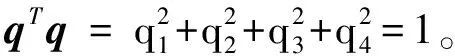
姿态矩阵和四元数的关系如下
(7)
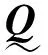
(8)
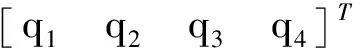
(9)
将式(7)代入式(2)得
(10)
令
(11)
(12)
(13)
则函数g(q)可以表示为关于四元数q的二次型函数
g(q)=qTKq
(14)
式中
(15)
考虑到式(4)的约束条件,利用拉格朗日乘子法可以证明[8]使g(q)达到最大的四元数恰好是矩阵K的最大特征值所对应的特征向量,即
Kqopt=λmaxqopt
(16)
如果直接计算,就需要求出矩阵K的所有特征值和特征向量,然后找到最大特征值所对应的特征向量,即为所求最优四元数qopt,把其代入式(9)即可求出姿态矩阵。
3. 迭代求解特征值法
定义Gibbs向量Y如下
Y=Q/q=ntan(θ/2)
(17)
则四元数q可以用Gibbs向量Y表示为
(18)
则式(14)可以变形为
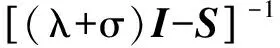
(19)
λ=σ+Z·Y
(20)
将式(17)代入式(18)得
(21)
若ξ是任意方阵S的特征值,则它们满足如下关系
det|S-ξI|=0
(22)
式(22)可以表示为如下形式
-ξ3+2σξ2+κξ+Δ=0
(23)
式中,σ=0.5tr(S)=tr(B);κ=tr(adjS);Δ=detH。
根据Cayley-Hamilton原理,S满足如下等式
S3=2σS2-κS+ΔI
(24)
对式(24)变形可以得到如下等式
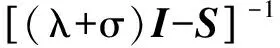
(25)
式中,α=λ2-σ2+κ;β=λ-σ;γ=(λ+σ)α-Δ。
把式(25)代入式(21)并整理,得
λ4-(a+b)λ2-cλ+(ab+cσ-d)=0
(26)
式中,a=σ2-tr(adjS);b=σ2+ZTZ;c=detS+ZTSZ;d=ZTS2Z。
对上式利用迭代方法即可求出λ,然后将其代入式(18)、式(19)求得最优四元数。为了防止迭代发散和加快收敛速度,选用牛顿下山法作为迭代方法,该方法同时具有牛顿法和下山法的优点,即在下山法保证函数稳定下降的前提下,用牛顿法加快收敛速度。
其迭代公式为
(27)
式中,ω为下山因子,ω的取值从1开始逐次减半直至满足|f(xk+1)|<|f(xk)|。
关于λ迭代初值的选择,把式(16)代入式(14)并考虑式(2)得
(28)
从上式可以看出,λmax≈1,因此用1作为初值比较合理。
三、试验分析
本节将分别用奇异值分解方法(方法1)、求解所有特征值和特征向量方法(方法2)和直接求解最大特征值方法(方法3)对仿真基线数据进行处理,然后对各种方法的计算精度和代价函数进行分析。
选取载体坐标系下的基线W1、W2、W3、W4、W5、W6如下
姿态矩阵为

如果没有误差,则V1、V2、V3、V4、V5、V6应为
由于传感器观测存在误差,V1、V2、V3、V4、V5、V6不可能准确地获得上面的数值。假设基线误差服从零均值高斯分布,根据基线精度和姿态角精度的关系[10],并参考实际测量中姿态角的测量精度,在V1、V2、V3、V4、V5、V6中都加入均值为零、标准差为0.000 1 m的随机白噪声。对每种情况进行100次仿真,并利用上述3种方法对仿真数据进行解算。
解算结果的精度如何,需要根据罚函数进行判定,根据3种方法对100个历元解算结果得到的罚函数平均值见表1,各个历元的罚函数如图1所示。

表1 3种方法罚函数平均值
从表1可以看出,3种方法的罚函数平均值都很小,且3种方法的罚函数平均值完全相同,说明姿态解算的精度很高。

图1 3种方法的罚函数
从图1可以看出,3种方法的罚函数完全重合,这说明它们的定姿结果很可能完全相同。为了进一步分析,下面将每个历元的姿态角都计算出来,并将其与真值进行比较。3种方法计算得到的航向角、俯仰角、翻滚角与真值的误差如图2—图4所示,姿态解算结果的平均值与真值的差值及标准差见表2。

图2 航向角与真值误差
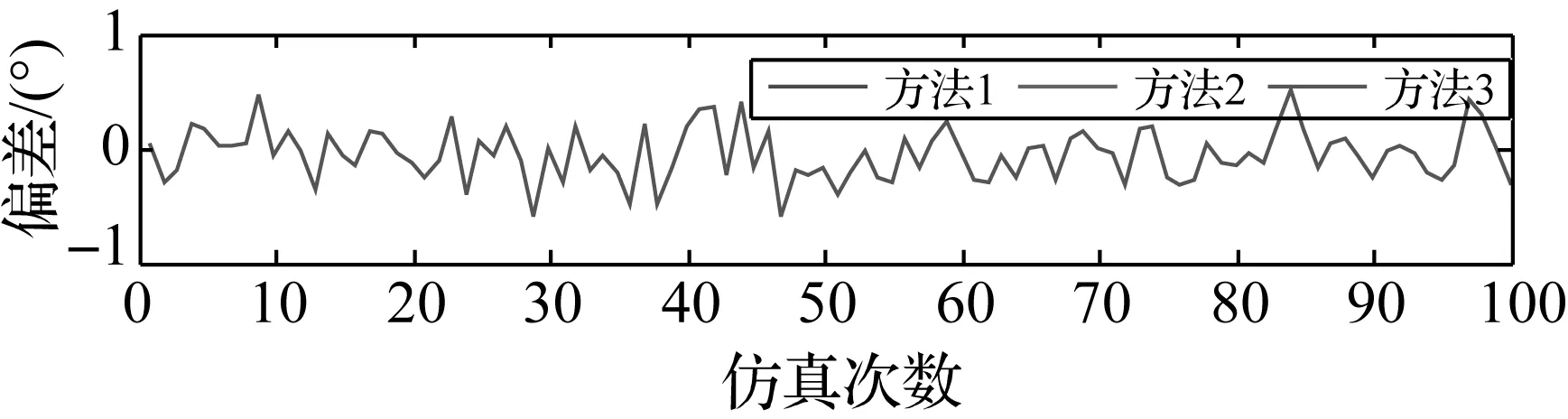
图3 俯仰角与真值误差
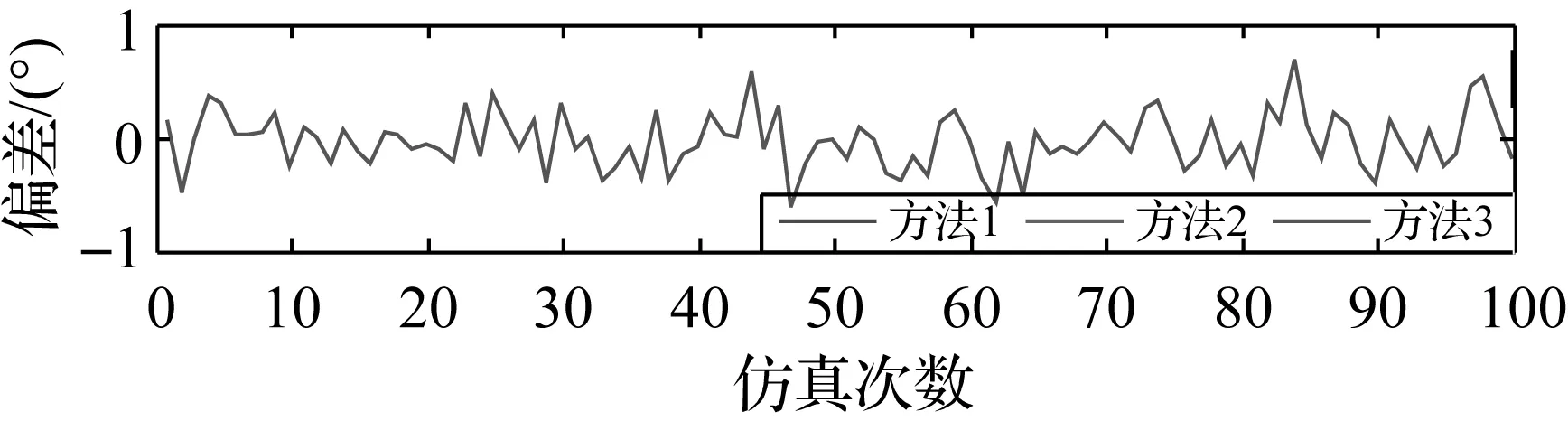
图4 翻滚角与真值误差

表2 姿态解算结果的标准差和平均值与真值之差 (°)
通过图2—图4和表2可以看出,3种方法的定姿结果完全相同,航向角、俯仰角和翻滚角的定姿精度都能达到0.2°左右,最大偏差不超过0.5°。
四、结束语
本文分析了两种常用的最优化定姿方法及其存在的问题,提出了一种基于四元数的最优姿态解算方法。该方法首先利用牛顿下山法求解大特征值,然后根据特征值和最优四元数的关系求解最优四元数,从而求出姿态参数。基于奇异值分解的定姿方法由于需要对矩阵进行奇异值分解,对计算机要求较高;第二种方法需要求解出所有的特征值和特征向量,然后找到最大特征值对应的特征向量,该方法由于涉及矩阵特征值和特征向量的求解,因此对计算机要求也较高。本文所提方法由于只涉及对矩阵和向量的基本运算,因此对计算机的要求较低,便于编程实现。通过对仿真数据解算结果的分析可以发现:本文所提方法和前两种最优化方法的解算结果一致,完全可以达到要求的定姿精度。
参考文献:
[1] BAR-ITZHACK I Y, HARMAN R R. Optimized TRIAD Algorithm for Attitude Determination[J].Journal of Guidance Control and Dynamics, 1997, 20(1):208-211.
[2] FARRELL J L, STUELPNAGEL J C, WESWNER R H, et al. A Least Squares Estimate of Spacecraft Attitude[J].SIAM Review,1966,8(3):384-386.
[3] DAVENPORT P B. A Vector Approach to the Algebra of Rotations with Applications[R].Washington D.C.:NASA,1965.
[4] BLACK H D.A Passive System for Determining the Attitude of a Satellite[J]. AIAA Journal,1964,2(7):1350-1351.
[5] Wahba G.A Least Squares Estimate of Satellite Attitude, Problem 65.1[J].SIAM Review,1965,7(3):409.
[6] MARKLEY F L. Attitude Determination Using Vector Observation and the Singular Value Decomposition [J]. The Journal of the Astronautical Sciences. 1988, 36(3): 245-258.
[7] MARKLEY F L. Attitude Determination Using Vector Observation: A Fast Optimal Matrix Algorithm [J].The Journal of the Astronautical Sciences(S0021-9142). 1993, 41(2): 261-281.
[8] KEAT J E. Analysis of Least-square Attitude Determination Routine DOAOP[R].[S.l.]:Computer Science Corp., Report,1977.
[9] 程国采. 四元数法及其应用[M].长沙:国防科技大学出版社,1991.
[10] LU G. Development of a GPS Multi-antenna System for Attitude Determination[D].Calgary, Canada:The University of Calgary,1995.

