物理量的度量模型及其在测绘学中的应用

陈仲怀，钟业勋，，胡宝清

(1. 广西壮族自治区测绘地理信息局，广西 南宁 530023； 2. 广西师范学院 北部湾环境演变与资源利用省部共建教育部重点实验室，广西 南宁 530001)

地球信息是指关于地理实体，如资源、环境、经济和社会诸要素的物质和能量的性质、特征和状态表征的知识[1]。地球信息是制作地图的依据和源泉，而获取地球信息总离不开对地物的空间位置、形状、大小、质量、状态等的度量。本文是笔者关于地物物理量的度量模型及其在测绘学中的应用的研究。

一、常用物理量的计算单

1960年10月，第11届国际计量大会确定了国际通用的国际单位制，简称SI制。SI制共有7个基本单位[2]，见表1。

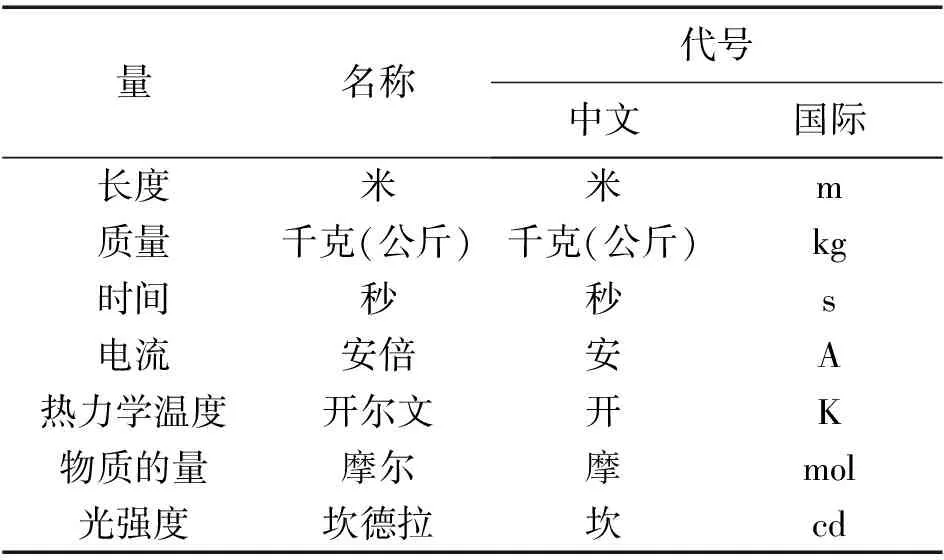
表1 国际制(SI)基本单位

二、物理量度量模型

从拓扑学得知，一维、二维和三维空间都是度量空间。对于三维度量空间(R3,d)的任何子集ai都叫做空间(R3,d)的点集。设ai∈(R3,d)，i为ai的物理特性，i的标号集为I，i∈I，I={物理特性}。因此ai的空间坐标、时间坐标、质量等都属于I范畴。在度量空间(R3,d)中，∀ai∈(R3,d),∃i∈ai和i0∈(R3,d)，i≠i0⟹d(i,i0)>0，将度量单位Bi与d(i,i0)进行比较，即得ai度量结果Qi

Qi=d(i,i0)/Bi

(1)

i∈I的关系表明，式(1)可对多种ai的物理特性i进行度量。式(1)为度量对象ai的物理量i的度量模型。

三、地物物理量的度量模型在测绘学中的应用

1. 地物空间位置度量

任何事物，无论是物质的(如道路)或是非物质的(如宗教信仰)，都是一种地理现象，或称空间现象，它们都具有位置，因而可以表示在地图上。数据间的位置关系，通常称为地理序列(geographical ordering)，是最重要的基本性质[3]。地物空间位置的确定，必须将其置于一定的坐标系中。在大地测量中，地面点的位置常使用大地坐标系。大地坐标系是通过一个辅助面(参考椭球面)定义的。大地坐标系中的参考面是长半轴a以短半轴b为旋转轴的椭球面。椭球面的中心与直角坐标系的原点重合，短半轴与直角坐标系的Z轴重合。大地坐标系的纬度B为过空间点p的椭球面法线与XOY平面的夹角。大地经度L为ZOX平面与ZOp平面的夹角，自ZOX平面起算，右旋为正。大地高H为过p点的椭球面法线上自椭球面至p点的距离，以远离椭球中心为正[4]。

在ai=p(B,L,H)的大地坐标系中，i有3个分量：i∈B∈[0°，±90°]⟹i0=0°(赤道)，i∈L∈[0°，±180°]⟹i0=0°(零子午线)，i∈H∈[法线内外]⟹i0=0(椭球面)。纬度B和经度L的度量单位Bi均为“度”，1度等与圆周的1/360。 大地高H的度量单位Bi为米(m)。度量结果Qi即度量对象ai以纬度B、经度L及大地高H表示的大地坐标。

2. 高程度量

在大地测量中，将重力位为常数的面定义为重力等位面。大地水准面是与平均海水面紧密相关的重力等位面。由于大地水准面与整个地球较为接近，因此通常用大地水准面作为高程基准面[5]。在高程度量中，ai=i∈{空间点}，i0=0(大地水准面)，度量单位Bi为米(m)。度量结果Qi为度量对象ai的以度量单位m表示的高程。同一度量对象在不同的度量基准下其高程也不同。如青岛市观象山上的水准原点，在“1956黄海高程系”中的高程为72.289 m,而在“1985国家高程基准”中则为720.260 m, 原因是后者比前者升高了29 mm。i>i0⟺高程为正；否则高程为负，如新疆吐鲁番盆地低于海平面地方的高程。

3. 一维、二维和三维度量

在度量空间中，度量对象ai与度量单位Bi必须同维，即满足

∀ai∈Rn⟹Bi∈Rnn=1,2,3

(2)

通常n=1时属线性度量，Bi属长度单位，如米(m)、千米(km)等， 可度量道路的里程等；n=2时属面积度量，Bi属面积单位，如平方米 (m2)、平方千米(km2)等， 可度量土地的面积等；n=3时属体积度量，Bi属体积单位，如立方米(m3)、立方千米(km3)等， 可度量土方等地理实体的体积。

4. 时间度量

空间和时间是物质固有的存在形式。度量两个时刻之间的间隔长短的物理量叫做“时间”，它表征物质运动过程的广延性、间断性和顺序性。时间是天体及其物体的自然属性，是一种实实在在的运动形式，必不能为虚。由于天体运动是不可逆的，因此也不能为负，仅有过去、现在、将来而已。时间、空间和物质运动的不可分离性已被狭义相对论证实。我们的世界是四维连续区。1908年，德国数学家闵可夫斯基(Minkowski)为四维时空提出了数学框架，即闵可夫斯基几何，此时的时间和空间坐标满足[6]

l2=x2+y2+z2-t2

(3)

按照物理学的说法，三维空间中的“事件”就成为四维“世界”的存在。即∃ai∈R3⟹ai≠∅⟹tj>0|ai,ti∈R4。这一蕴涵关系表明，空间非空性和时间非负性是物质存在的充要条件。设T1为过去，T2为现在，T3为将来，“存在”的定义为[7]

C={ai,ti|ai≠∅∧ti>0，ai,ti∈T1∨T2∨T3}

(4)

C⊃ 过去存在(ai,ti∈T1)，现实存在(ai,ti∈T2)，将来存在(ai,ti∈T3)

由于物质存在的空间非空性和时间非负性条件，使任何空间存在物ai≠∅必有大于零的寿命ti，从而有其创生时刻ti0和消亡时刻ti1，两者间的“距离”d(ti1-ti0)=ti就是ai的寿命。这样，按式(1)，ai的寿命为

Qi=d(ti1,ti0)/s

(5)

式中，Qi就是ai的以秒为时间单位的寿命。

不同的事物一般使用不同的度量单位，如动植物、社会经济事件等，常用“年”为度量单位度量；地质年代往往用“万年” 、“百万年”为度量单位。

5. 质量度量

质量是物体所含物质的度量。根据使物体产生一个确定加速度所需要的力定义的该物体的物质数量，称为惯性质量。根据物体施加的万有引力定义的该物体所含的质量称为引力质量。现代物理证明，这两种质量完全相等，这就是所谓的马赫原理[8]。惯性质量和引力质量等价的事实成了广义相对论的重要依据。在质量度量中，质量i∈ai，i0=0为度量基准，Bi=kg(千克)为度量单位，Qi=d(i,i0)/kg为度量对象ai以Bi=kg(千克)为单位表示的质量。

质量和重量有联系又有区别。同一物体在哪里的质量都是一样的，而重量则与物体所处的位置有关。同一物体，在地球的两极因其离心力最小，离地心较近，因而会重些；在赤道上因离心力最大且与地心引力方向相反，其重量比在两极轻。1000 g的物体放到月球上，就只有160 g了，原因是月球的引力场比地球的引力场小得多。

四、结束语

对地物物理量的度量是获得地物的空间和物理

特性的相关信息的必要手段。地物物理量的度量模型由度量对象ai、度量基准ai0、度量单位Bi和度量结果Qi构成，度量对象ai包含多种性质i，即i∈ai⟹i0∈ai0。通过测绘学中的坐标、高程、时间、质量等实例，证明地物物理量的度量模型有实用价值和科学解释功能。

参考文献：

[1] 承继成，林晖，周成虎，等.数字地球导论[M].北京：科学出版社，2000.

[2] 测绘字典编辑委员会.测绘词典[M].上海：上海辞书出版社，1981.

[3] 罗宾逊，塞尔，莫里逊，等.地图学原理[M].北京：测绘出版社，1989.

[4] 程鹏飞，成英燕，文汉江，等.国家大地坐标系实用宝典[M].北京：测绘出版社，2008.

[5] 宁津生，陈俊勇，李德仁，等.测绘学概论[M].武汉：武汉大学出版社，2004.

[6] 阿尔伯特.爱因斯坦.相对论[M].重庆：重庆出版社，2009:189.

[7] 钟业勋，童新华，韦清嫄.地物性质和外形及其在地球椭球面上的投影的数学定义[J].桂林理工大学学报，2012,32(4)：528-531.

[8] 约翰.格里宾，黄麟译.大宇宙百科全书[M].海口：海南出版社，2001.