基于Snakes算法的道路要素移位软件模块

刘远刚，郭庆胜，孙雅庚，郑春燕

(1.武汉大学 资源与环境科学学院，湖北 武汉 430079； 2. 长江大学 地球科学学院，湖北 荆州 434023；3. 武汉大学 测绘遥感信息工程国家重点实验室，湖北 武汉 430079； 4. 嘉应学院 地理科学与旅游学院，广东 梅州 514015)

一、引 言

地图综合中的移位是一种为了保持要素之间的空间关系，保证要素的清晰易辨性或适应地图上的其他要素，而进行的解决地图要素间的冲突的地图综合操作。国内外关于地图要素移位的研究已经有了较长的历史，并提出了众多有效的算法[1-9]。其中 Burghardt和Meier(1997年)提出的基于Snakes的地图要素移位算法是一种非常适合线状要素移位的全局最优化算法，该算法把计算机视觉中已得到广泛应用的Snakes模型引入到地图综合领域，可有效地控制移位引起的后继冲突问题；Bader(2001年)、Galanda(2003年)和吴小芳(2005年)等多位学者对该算法进行了改进，并将其应用于线状要素移位和变形、多边形要素的移位、放大和夸大等操作[10-13]。本文采用C#编程语言和ArcGIS Engine二次开发组件，设计并实现了一种基于Snakes算法的道路要素移位软件模块。该模块针对道路要素移位的应用需求，采用面向对象的设计思想，实现了Snakes移位算法的数据模型、逻辑结构和算法流程，从而为Snakes移位算法的研究和应用提供软件支持。

二、Snakes移位算法基本原理

在基于Snakes的地图要素移位算法中，能量的描述均由最基本的移位量表示，将曲线要素的几何特征变化产生的能量作为内部能量，将空间冲突产生的排斥力作为外部能量，通过对内外能的计算，获得能量最小时的道路移位后的最优形状和位置。公式(1)是移位量的计算公式，其中l表示线的长度，(x0，y0)表示原始线的坐标，(x,y)表示线移位后的坐标，d(s)是移位量的参数表达；公式(2)是总能量计算公式，其中E(d)是总能量，Eint是内部能量，Eext是外部能量；内部能量由公式(3)求出，其中d′(s)和d″(s)分别是移位量d(s)关于s的一阶导数和二阶导数，反映了由于移位而产生的形状变化的大小，α(s)和β(s)参数决定Snakes模型的弹性和刚性，反映模型的属性，对移位效果有一定的控制作用；外部能量由产生冲突时地图符号的重叠产生，其值与重叠的大小成正比，由它促使线移动变形，从而解决冲突。

s→d(s)=(x(s)-x0(s),y(s)-y0(s))T,0≤s≤l

(1)

(2)

Snakes模型的原则是保持内能和外能之和的总能量值最小，因此需求解公式(2)中的E(d)取最小值时曲线各处的移位量。利用欧拉方程、有限元方法，并经过一系列变换，求得矩阵方程公式

Kd=f

(4)

式中，K是刚度矩阵；d是由曲线上各点处移位量及其一阶导数组成的移位向量，是方程的未知数；f是由曲线上各点处所受外力计算得到的向量。根据有限元方法，曲线上每一线段上对应的局部矩阵KL、dL、fL的计算方法如下(以x轴方向为例，y轴方向类似)

式中，α、β为α(s)、β(s)的常量形式；h为线段的长度；x0、x1为线段起点和终点处的坐标；d(x0)和d(x1)表示两点处x方向移位量；d′(x0)和d′(x1)表示两点处x方向移位量的一阶导数；f(x0)和f(x1)表示两点处所受外力在x方向上的分量。

对于整个道路网，需要对每一条线段分别计算局部矩阵，并依次将局部矩阵聚集到全局矩阵K、d、f中，最后分别对x和y方向上的全局矩阵方程求解，得到各点的移位向量。需要注意的是，K是奇异矩阵，无法求得其逆矩阵，导致无法直接对方程进行求解。因此，需要在矩阵中增加边界条件，将奇异矩阵K转换为常规矩阵，使之可解。另外，如果冲突区域目标不是很密集，冲突可能在一次操作中就得到解决；但实际上大多数的冲突区域情况复杂，参与冲突的目标较多，一次操作并不能完全解决所有的冲突，此时就要多次操作，逐步解决冲突。采用迭代最优化过程逐步解决所有冲突的计算方法如下

(E+γK)d(t)=d(t-1)+γf(t-1)

(8)

式中，E是单位矩阵；t为迭代次数；d(t)与d(t-1)分别是第t次的移位向量和第t-1次的移位向量；f(t-1)是第t-1次的各点处的受力向量；γ为迭代步长。

三、道路要素移位软件模块的设计与实现

该软件模块在Visual Studio 2010开发环境下，采用C#语言和ArcGIS Engine 10.0二次开发组件进行集成开发。地图显示功能和数据存取功能借助ArcGIS Engine提供的相关组件实现，数据结构和算法逻辑自主开发完成，其总体上分为主程序和Snakes移位算法模块两部分(如图1所示)。主程序是基于ArcGIS Engine组件的窗口应用程序，实现了地图显示和浏览、图层管理、算法全局参数交互设置和地图要素集存取等功能；Snakes移位算法模块用于实现整个算法的业务逻辑，主要包括道路网数据模型、算法全局参数列表和算法逻辑实现几个部分。道路网数据模型定义了道路网中所包含的道路对象、道路顶点对象、道路端点对象，以及三者之间的关联关系，且每种对象都以类进行封装，并设计了各自的属性和方法；算法全局参数列表包括整个算法的各项参数，如形状参数、迭代步长、迭代次数、道路符号设置、目标比例尺等；算法逻辑实现是对Snakes移位算法的实现，包括计算刚度矩阵、计算外力向量，以及矩阵加、减、乘、除、求逆等基本运算的实现。主程序与Snakes移位算法模块之间通过可视化界面进行数据交换。主程序调用算法模块时，系统先向算法模块中的全局参数列表写入用户设置好的全局参数，并将ArcGIS Geodatabase中的原始要素集导入算法模块，建立对应的道路网数据集；然后将全局参数作为输入条件运行算法逻辑实现部分对道路网数据集进行移位处理，处理后的结果再导出为新的ArcGIS Geodatabase要素集(结果数据集)显示到地图窗口中。

在基于Snakes的道路要素的移位算法中，必须先计算出整个道路网的刚度矩阵和受力向量，然后解矩阵方程得到移位向量。对于前者，不仅需要用到道路网中所有道路顶点的坐标数据，而且需要知道道路之间的拓扑关联信息，否则无法完成不同道路的刚度矩阵的聚合。根据上述刚度矩阵和受力向量的数值计算方法的需要，笔者设计了一种简单的道路网数据模型。图2中的道路网模型主要定义了RoadNetWork、Road、PointCoord和ConnNode几个类，分别用于描述与道路网、道路、道路网中的顶点和端点几类对象的属性和方法。这几个类之间相互关联形成一个包含了基本拓扑信息和坐标信息的道路网模型。在该模型中，一个道路网由道路列表、顶点列表和端点列表构成；一条道路包含一个起点和一个终点(统称为端点)，包含多个(两个以上)顶点；每一个端点同时也是一个顶点，它可以作为道路的起点或终点，与多条(一条以上)道路相关联。另外，RoadGrade类用于描述道路的等级属性特征，在算法中它是设置单条道路的形状参数的基本依据。图2中的AlgSnakes类是Snakes移位算法逻辑的实现，该类中定义了Snakes算法的全局参数列表与所有的计算方法和计算流程，具体见表1和表2。其中Run_Alg_Snakes方法通过对其他计算方法的调用实现了Snakes移位算法的基本流程。

图1 总体结构图

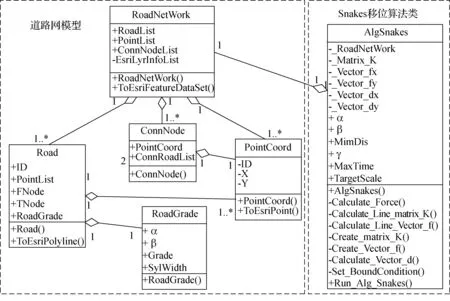
图2 UML类图

表1 AlgSnakes属性说明

表2 AlgSnakes方法说明

图3是Snakes算法用于道路要素移位的基本流程，具体步骤包括：①初始化，设置各项全局参数的初始值和创建道路网数据模型。全局参数包括形状参数、最大迭代次数、迭代步长、目标比例尺、道路符号宽度、地图目标间最小间隔等；道路网数据模型通过导入的道路要素集数据得到。②计算道路网刚度矩阵，先根据式(5)计算出组成道路要素的所有线段的局部刚度矩阵，然后根据道路顶点下标将其依次累加到全局刚度矩阵中对应的元素上，最终得到道路网的全局刚度矩阵。③计算各点的受力，如果所有顶点的受力均为0，则直接结束，否则执行下一步。④计算道路网受力向量，先根据式(7) 计算出组成道路要素的所有线段的局部受力向量，然后根据道路顶点下标将它们依次累加到全局受力向量中对应的元素上，最终得到道路网的全局受力向量。⑤跟据式(8)解矩阵方程，得到新的移位向量。⑥用新的移位向量更新道路网中各坐标点的值，判断是否达到迭代最大次数，若达到则结束，否则迭代次数增加1次，然后转到步骤③继续执行。

图4和图5为本文所实现的软件系统运行截图。图中所用试验数据是通过ArcGIS矢量化得到的来源于Google Map上某山区的部分道路网。在进行移位操作之前，已经完成线目标的化简、弯曲合并等处理。图4是对算法全局参数进行设置的对话框，本例中目标比例尺为1∶50万，形状参数α和β分别设置为10 000 000和1 000 000，图上最小间隔为0.2 mm，最大迭代次数为2，迭代步长为0.1，各类要素符号宽度设置分别为高速公路2.0 mm、国道1.8 mm、省道1.2 mm、河流中心线0.7 mm。图5是采用该模块对试验数据实施移位操作得到的最终效果。为了便于对比，将移位前后的道路网同时显示于地图窗口中，从中可以看出，原本处于冲突区域的道路路段已移出冲突范围，且道路的整体形状保持较好，道路间的拓扑关系也未被破坏，整体效果良好。

图3 算法流程图

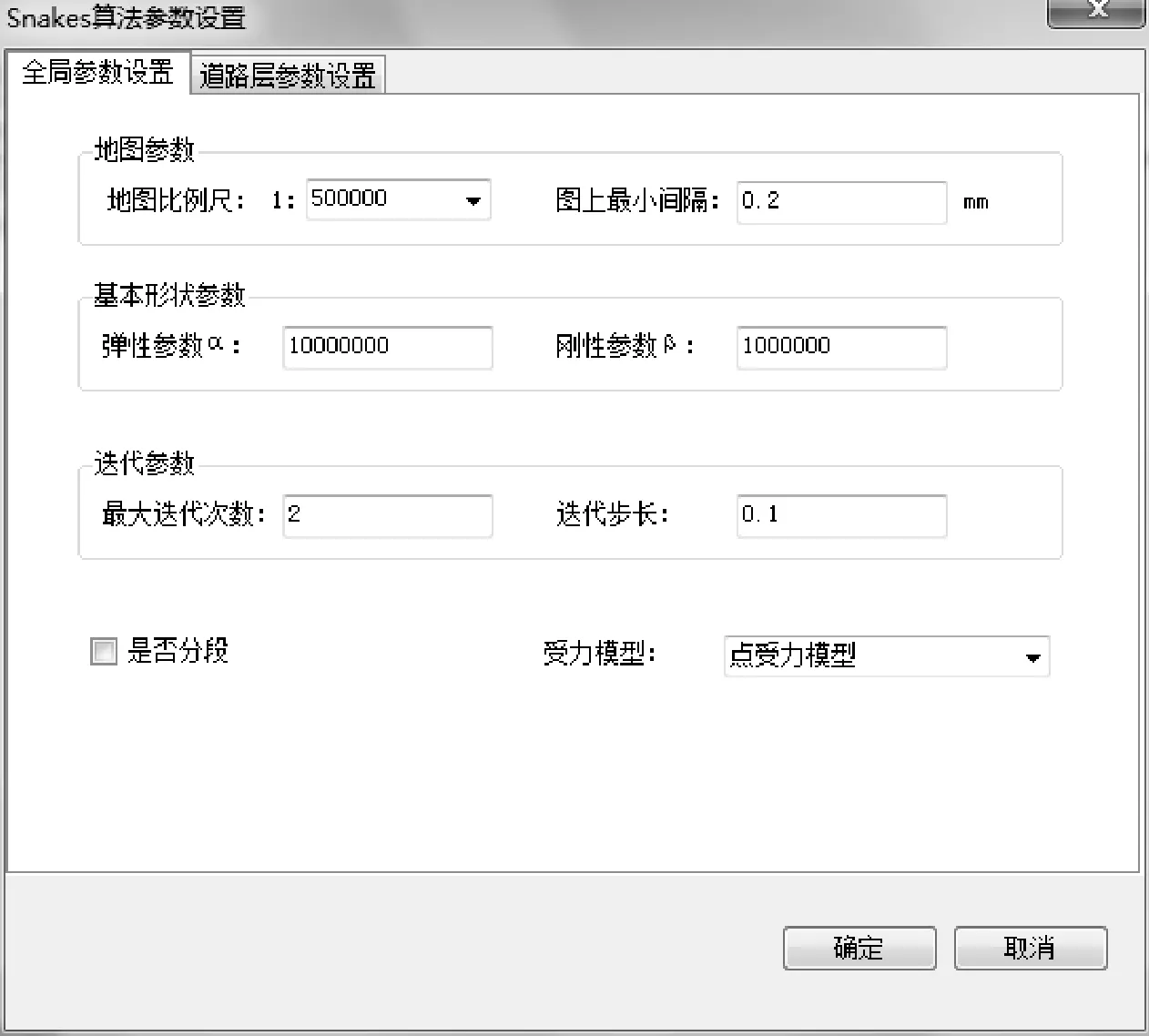
图4 Snakes移位算法参数设置

四、结束语

基于Snakes模型的地图要素移位算法是一种适合线状要移位的全局最优化算法，该算法具有成熟的理论基础。本文采用C#编程语言和ArcGIS Engine二次开发组件，设计并实现了一种基于Snakes算法的道路要素移位软件模块。使用该模块对道路网进行移位，在算法中的形状参数设置合适时，可同时解决道路网中多条道路之间的冲突问题，且能较好地保持道路的形状特征。通过本软件模块的开发和试验数据的测试，进一步验证了基于Snakes的移位算法全局性最优化的优点，同时也发现了该算法在参数设置方面自动化程度低的缺点，为算法的改进指明了方向；而且模块采用了面向对象的程序设计方法和独立于ArcGIS平台的数据模型，具有较好的可移植性和可扩展性，有利于今后进一步的改进和应用。

参考文献：

[1] LICHTNER W.Computer-assisted Processes of Cartographic Generalization in Topographic Maps[J]. Geo-Processing, 1979,1(1):183-199.

[3] RUAS A. A Method for Building Displacement in Automated Map Generalisation[J]. International Journal of Geographic Information Science, 1998,12(7):789-803.

[4] HØJHOLT P. Solving Local and Global Space Conflicts in Map Generalization: Using a Finite Element Method[J].Cartography and Geographic Information Science, 2000, 27(1):65-73.

[5] WATE J M, JONES C B. Conflict Reduction in Map Generalization Using Iterative Improvement[J]. GeoInformatica,1998, 2 (4):383-407.

[6] HARRIE L E. the Constraint Method for Solving Spatial Conflicts in Cartographic Generalization[J].Cartography and GIS, 1999, 26(1):55-69.

[7] BADER M. Energy Minimization Methods for Feature Displacement in Map Generalization[D]. Zurich: University of Zurich, 2001.

[8] WILSON I D, WARE J M, WARE J A.A Genetic Algorithm Approach to Cartographicmap Generalization[J]. Computers in Industry,2003,52 (3):291-304.

[9] 艾廷华.基于场论分析的建筑群的移位[J].测绘学报,2004,35(1):89-94.

[10] BADER M. Energy Minimization Methods for Feature Displacement in Map Generalization[D]. Zurich: University of Zurich, 2001.

[11] GALANDA M.Automated Polygon Generalization in a Multi Agent System[D]. Zurich:University of Zurich,2003.

[12] 吴小芳,杜清运, 胡月明，等. 基于改进Snake模型的道路网空间冲突处理[J].测绘学报,2008,37(2):224-229.