CGCS2000独立坐标系与原城市独立坐标系融合问题的研究

李 东，毛之琳，王文利，齐 芮

(国家测绘地理信息局大地测量数据处理中心，陕西 西安 710054)

一、引 言

一般独立坐标系的设计原则是寻找坐标系最佳参数，让满足区域内长度变形不超限的范围最大化。目前基于CGCS2000[1]新建城市独立坐标系(以下简称2000独立坐标系)正是遵循此原则，但是没有顾及或无法解决与原先城市独立坐标系(以下简称原独立系)兼容问题，使得两者坐标差异较大，原有测绘成果需全部转换到2000独立坐标系下方可使用。虽然2000独立坐标系具有众多优越性[2]，但转换工作量及费用之大，让业界望而却步，成为CGCS2000在城市推广的瓶颈问题。2000独立坐标系是以全球定位系统作为获取成果的主要手段，其大地控制点的相对精度为10-7～10-8[3]，而原独立系多数成果是以三角测量获取的，其大地控制点的相对精度为10-6，两者成果精度存在一定差异。另外，现有大多数城市独立坐标系是基于1954北京坐标系建立的，由于新旧坐标系基于椭球不同，即使采用同样模型和方法，产生的坐标也具有较大差异，因此新旧坐标系差异是存在的，如何使两者坐标差达到最小，减少转换工作量是解决问题的关键。本文提出一种建立2000独立坐标系与原独立系相融合的方法，使两者坐标差达到地形图允许误差，使原有大部分地图无需转换，直接在新坐标系下使用，基本解决了新旧坐标系融合问题。

二、建立2000独立坐标系方法

1. 建立2000独立坐标系原则

寻找坐标系最佳参数，使新旧城市独立坐标系坐标相差最小，达到地形图允许误差，其次再考虑限制长度变形超限问题。

2. 地形图最大允许误差

《城市测量规范》(CJJ/T 8—2011)[4]规定：“6.3.2图根点相对于图根起算点的点位中误差，不得大于图上0.1 mm；6.1.6平地、丘陵地平面点位中误差限差为图上0.5 mm。”从规范可知，图上0.1 mm误差，实地误差为0.1M(M为测图比例尺分母)，单位为毫米；测图平面点位最大允许误差为0.5M，单位为毫米(见表1)。考虑原有地形图已有误差，为了保证在新坐标系下具有可靠精度，本文提出方法规定：以两坐标系平均坐标差小于0.1M实地误差作为衡量标准。

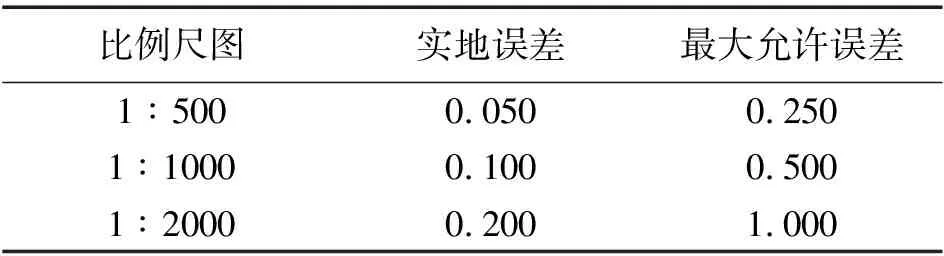
表1 各种比例尺地图误差 m

如1∶500地形图，图上0.1 mm误差，实地误差为0.05 m，最大允许误差0.250 m，当两坐标系平均坐标差 ≤ 0.05 m，可满足1∶500地形图直接在新坐标系下使用的要求。

3. 独立坐标系参数和模型分析

(1) 独立坐标系参数分析

独立坐标系参数一般包含椭球参数、高斯投影中央子午线、投影面及坐标原点。由于2000独立坐标系和原独立系基于椭球不同，为了减少两者坐标差，中央子午线和原点要保持一致，从高斯投影公式(1)分析，主要影响y值大小是第一项，中央子午线保持一致，两坐标差相对较小。

(1)

式中，l=该点的经纬度值-中央子午线。

(2) 常用独立坐标系模型分析

① 椭球膨胀法

以投影面的大地高ΔH作为椭球平均曲率半径的变动量，有

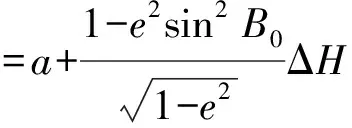
(2)

则有

② 比例缩放法

由平面坐标变换为独立坐标公式

式中，q=H/Rm为缩放系数；H为抬高投影面高度；(X0,Y0)为原点坐标。

③ 模型分析

对于抬高投影面城市独立坐标系，分别采用椭球膨胀法与比例缩放法，产生坐标有几十米非线性差异。虽然新旧坐标系基于椭球不同，但采用相同模型，可减少差异。

4. 检验数据及精度分析

在一定区域内，收集CGCS2000坐标和原独立系重合控制点坐标作为检验数据，要求重合点分布在区域范围四周和内部，具有一定代表性。检验数据作为衡量2000独立坐标系是否达到设计要求的依据，其精度决定两坐标系的符合程度，不能含有异常点，可利用坐标转换方法对其进行精度检验。常用坐标转换模型有Bursa七参数和二维四参数模型[3，5]。

(1) Bursa七参数模型

式中，ΔX、ΔY、ΔZ为3个平移参数；ωX、ωY、ωZ为3个旋转参数；m为尺度因子；(XN，YN，ZN)为目标坐标系坐标。

(2) 二维四参数转换模型

式中，(xT,yT)为目标坐标系高斯平面坐标；(xS,yS)为源坐标系高斯平面坐标；Δx、Δy为平移参数；θ为旋转参数；m为尺度参数。

(3) 坐标转换精度估计

精度估计是通过转换残差反映，是利用重合点的回代误差，评定转换精度。

X和Y坐标转换中误差

转换坐标中误差(转换残差)

式中，n为重合点个数；参加转换重合点的vi=已知坐标 - 转换坐标。

三、实例分析

西部某市原独立系是基于1954北京坐标系椭球参数，中央子午线为任意带，抬高投影面700 m，原点为4号点，采用比例缩放法。收集8个CGCS2000与原独立系重合控制点坐标作为检验数据，其分布基本覆盖控制区域四周和中央(如图1所示)。

1. 检验数据精度估计

采用Bursa七参数模型对检验数据进行精度估计，坐标转换残差为0.035 m，说明提取重合点数据精度较高，可作为检验数据(如表2、图2所示)。

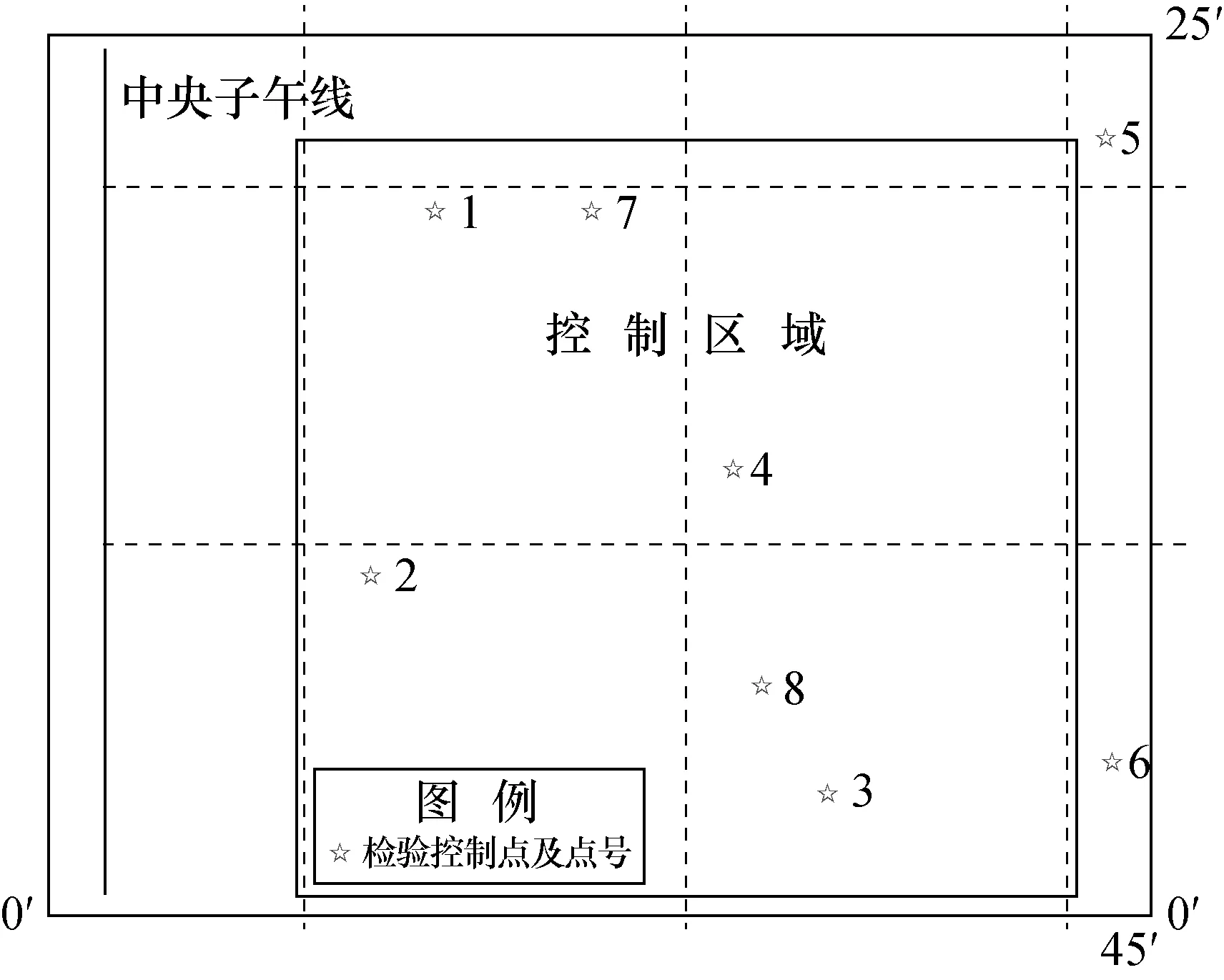
图1 检验数据分布图

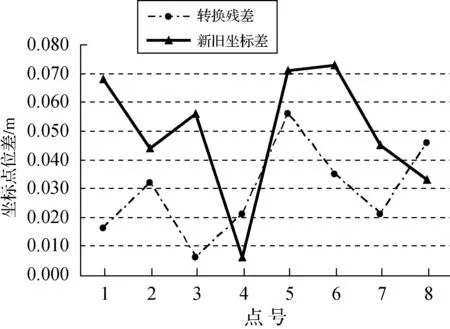
图2 坐标转换残差和新旧城市坐标系坐标差分布图

表2 2000独立坐标系与原独立系转换残差及新旧坐标差 m

2. 寻找建立2000独立坐标系最佳参数

以检验数据为依据，用相同比例缩放法模型，在原坐标系中央子午线±1°之间，且投影面在0～4000 m之间，寻找2000独立坐标系与原独立系符合最接近的参数。试算结果：当新旧坐标系原点和中央子午线一致、且长度变形较为接近时，两者坐标差最小，即两坐标系附合得最好。考虑到两坐标系基于不同椭球，在一般城市范围内两者坐标差接近常数，2000独立坐标系坐标与原独立系接近，需要加常数。新建2000独立坐标系参数见表3。

表3 2000独立坐标系参数

3. 结果分析

产生新旧坐标系平均坐标差为0.049 m，最大坐标差为0.073 m(见表2、图2)，新旧坐标系平均坐标差小于1∶500图实地误差，即0.049 m<0.050 m，满足1∶500以小比例尺地形图在2000独立坐标系下直接使用精度要求，仅需对控制点进行转换，说明新建立2000独立坐标系与原独立系具有较高的符合性。

四、结束语

1) 上述方法建立2000独立坐标系与原独立系坐标较为接近，极大减少了转换工作量，达到2000独立坐标系的设计目标。两坐标系符合程度主要与成果精度和控制范围有关，如果原独立系成果精度较差，与高精度成果将很难有较高符合性；如果控制范围较大，两坐标系坐标差不再接近一个常数，符合程度也随之降低。符合程度决定转换工作量。

2) 由于上述方法产生2000独立坐标系与原独立系长度变形基本相同，为了改善长度变形现状，可在大城市主要区域(成果较多)用上述方法建立2000独立坐标系,在其他区域可新增投影带，这样既可减少转换工作量，又能够有效限制长度变形超限。

3) 对于原先没有抬高投影面城市独立坐标系，也可用类似方法找到相应的解决途径，由于篇幅所限，将另文再叙。

本文提出的方法既发挥了2000独立坐标系的优越性，又较大减少了转换成果的工作量及成本，基本上解决了2000独立坐标系在城市推广的瓶颈问题。

参考文献：

[1] 陈俊勇．中国现代大地基准——中国大地坐标系统2000(CGCS 2000)及其框架[ J ]．测绘学报，2008，37(3)：269-271.

[2] 郭春喜，李东.基于CGCS2000建立城市相对独立坐标系统的方法[J].测绘通报，2012(10)：5-7，14.

[3] 程鹏飞，成英燕，文汉江，等.2000国家大地坐标系实用宝典[M].北京：测绘出版社，2008.

[4] 中华人民共和国住房和城乡建设部.CJJ/T 8—2011城市测量规范[M].北京：中国建筑工业出版社，2011.

[5] 杨元喜，徐天河.不同坐标系综合变换法[J].武汉大学学报：信息科学版，2001，26(6)：509-513.

[6] 施一民.现代大地控制测量[M]. 北京：测绘出版社，2003.