集成物流、能流和流分析的纸机干燥部建模

周艳明 刘焕彬 李继庚

(1.电子科技大学中山学院,广东中山，528402;2.华南理工大学制浆造纸工程国家重点实验室,广东广州，510640)

我国造纸工业的物耗、水耗和能耗都很高[1]。纸机干燥部(以下简称“干燥部”)是造纸过程能耗最大的工序[2]，约占造纸过程总能耗的67%以上[3]，占纸张生产成本的5%～15%[4]。在纸幅干燥设备中，多烘缸干燥部是目前应用最多的干燥设备，约占现有造纸干燥设备的85%～90%[5]。因此，通过研究多烘缸纸幅干燥过程，建立干燥部机理-实验模型和仿真系统，优化干燥部的设计及运行，对于提高干燥部能效，尤其是纸幅干燥过程的能效，从而降低造纸过程能耗，是一种行之有效的信息化手段。

在干燥部建模方面，Karlsson基于物料和能量平衡给出了一种多烘缸纸幅干燥的建模方法[6]。Nilsson[7]和Yeo[8]等人根据热质传递机理分别对多烘缸纸幅干燥过程进行了建模。鉴于纸张是一种多孔介质，Etemoglu等人也基于物料和能量平衡，提出了基于多孔介质理论的纸幅干燥模型[9]。在国内，周强等人从纸张干燥过程的原理出发，建立了纸幅干燥过程的数学模型，并采用遗传算法对烘缸干燥曲线进行优化[10]。沈胜强等人也基于多孔介质理论，建立了纸幅干燥过程的数学模型，对纸幅干燥过程进行了数值模拟和参数分析[11-13]。Kong等人基于物质和能量平衡对多烘缸纸机干燥部建立了静态能量模型[14]。林治作等人则专门针对纸幅干燥过程的建模进行了系统研究[15]。刘金星等人基于物料和能量平衡专门针对多烘缸纸机干燥部进行了建模和仿真[16]。

对干燥部的用能分析，Bujak基于能量平衡对生产瓦楞原纸的纸板机蒸汽系统的节能和热效率进行了分析[17]。Roonprasang为提高干燥性能对多烘缸干燥部进行了热力学分析[18]。Sivill等人对纸机干燥部的热回收系统进行了热力学模拟，并用换热网络对其能源效率进行了改善[19-20]。Kong等人从节能角度出发对涂布纸机干燥过程的废热集成进行了研究[21]。李玉刚等人则基于联立模块法，用NLP方法对纸机干燥部操作环境进行了参数优化[22]，并用过程参数优化方法，对纸机干燥部的节能进行了研究[23]。

1 单元模型

1.1 功能单元划分

1.2 干燥部各功能模块的建立

1.3 纸幅单元模型

该模块用于模拟湿纸幅在烘缸表面干燥过程纸幅物性参数变化，称之为纸幅模块。湿纸幅依靠烘缸提供的热量和气罩内热风发生传热传质过程，达到干燥纸幅的目的。它包含与烘缸接触干燥以及纸幅在烘缸之间的对流干燥。该模块较为复杂，因为它需要考虑纸幅干燥速率(蒸发水量)与蒸汽消耗、通风能耗(包括通风电耗)、蒸汽与空气的状态变量和主要的设备变量等关系。

1.3.1抽象模型

图1 含分析参数的纸幅功能模块的抽象模型

1.3.2数学模型

Fpi+Fhai=Fpo+Fhao

(1)

Fhaia=Fhaoa

(2)

Fhao=Fhai+Fvo

(3)

Epi+Ehai+Edi=Epo+Ehao

(4)

Expi+Exhai+Exdi=Expo+Exhao+Exd

(5)

式中，Fhaia、Fhaoa分别为Fhai、Fhao的绝干空气量，Fvo为湿纸幅蒸发水量。

已知进湿纸幅的Fpi、tpi、Rpi，进热空气的Fhai、thai、Rhai，出热空气的thao。根据文献[27]，计算进湿纸幅Epi、Expi的数学模型分别为：

Epi=FpiRpicpftpi+Fpi(1-Rpi)hw(Tpi,ppi)

(6)

Expi=FpiRpi[cpf(Tpi-T0)-T0cpfln(Tpi/T0)]+

Fpi(1-Rpi){[hw(Tpi,ppi)-h0]-

T0[sw(Tpi,ppi)-s0]}

(7)

式中，cpf为纤维的比热容(kJ/(kg·K))，hw(Tpi,ppi)为求水在温度Tpi、压力ppi下的焓h，sw(Tpi,ppi)为求水在温度Tpi、压力ppi下的熵s。

纸幅单元模型的关键在于如何求得湿纸幅蒸发水量、出纸幅的干度和温度。湿纸幅蒸发水量是根据纸幅在烘缸中的干燥速率(以下简称“纸幅干燥速率”)计算得到的。在烘缸的双面自由蒸发干燥区，纸幅受到对流干燥作用；在贴缸干燥区和压纸干燥区，纸幅受到接触干燥作用，因此，纸幅干燥速率又分为纸幅接触干燥速率和纸幅对流干燥速率。在实际建模中，对多烘缸往往进行分段处理，每段烘缸组包含的烘缸个数不同。在同一段烘缸组中纸幅对流/接触蒸发速率在不同烘缸之间是不同的。为减少模型的复杂性，假设同一烘缸段的对流/接触蒸发速率是相同的。

湿纸幅蒸发水量Fvo为：

Fvo=Fvod+Fvoj

(8)

式中，Fvod为同一烘缸段纸幅对流蒸发水量(kg/h)(见式(9))，Fvoj为同一烘缸段纸幅接触蒸发水量(kg/h)(见式(11))。

(1)烘缸段内纸幅对流蒸发水量的计算

烘缸段内纸幅对流蒸发水量Fvod可用式(9)计算得到：

(9)

式中，Wd为纸幅对流干燥蒸发水量(kg)，t为蒸发时间(h)，Vd为纸幅水分对流蒸发速率(kg/(m2·h))，Ad为单个烘缸对流蒸发面积(m2)，n为烘缸段内的烘缸个数。

纸幅对流干燥的干燥速率Vd服从道尔顿方程：

(10)

式中，ps为在水蒸发温度时的饱和蒸汽压(MPa)，pd为纸幅周围空气的水蒸气分压(MPa)，Ph为纸幅周围的大气压(MPa)，Kn为自由水表面蒸发系数(kg/(m2·h))。

(2)烘缸段纸幅接触蒸发水量的计算

烘缸段纸幅接触蒸发水量Fvoj可用式(11)计算得到：

(11)

式中，Wj为纸幅接触干燥的蒸发水量(kg)，Vj为纸幅水分接触蒸发速率(kg/(m2·h))，Aj为单个烘缸接触蒸发面积(m2)。

纸幅接触干燥的干燥速率Vj可由下式计算：

(12)

式中，ts为烘缸内饱和蒸汽温度(℃)，tp为烘缸表面纸幅温度(℃)，γ为蒸发水的汽化潜热(kJ/kg)，Kt为接触总的传热系数(kJ/(m2·h·℃))。

(3)烘缸段出口纸幅干度Rpo的计算

对于每个烘缸段，由质量守恒定律得：

(13)

(4)烘缸段出口纸幅温度tpo的计算

对于每个烘缸段，由能量守恒定律得：

(14)

式中，Q1为有效传热量(kJ/kg)，cpw为水的比热容(kJ/(kg·K))。

1.4 烘缸组模块

该模块用于模拟纸机中被划分的烘缸组，其作用是模拟饱和蒸汽进入烘缸组冷凝为纸幅干燥提供热量的过程。在这个过程中，饱和蒸汽经过烘缸组后变成二次蒸汽和冷凝水输出，同时伴随烘缸组的散热，这些热量传给气罩内的空气。

1.4.1抽象模型

含各种输入/输出物质分析参数的烘缸组模块抽象模型如图2所示。功能模块称为Dryer。其中，s表示比熵(kJ/(kg·℃))，下标s表示新鲜蒸汽(二次蒸汽)、w表示冷凝水、a表示空气、p表示纸幅。

图2 含分析参数的烘缸组功能模块的抽象模型

1.4.2数学模型

Fsi=Fso+Fwo

(15)

Esi=Eso+Ewo+Epo+Eao

(16)

Exsi=Exso+Exwo+Expo+Exao+Exd

(17)

已知进新鲜蒸汽的压力psi、出二次蒸汽的压力pso、乏汽比Rso(%)、烘缸传给纸幅的能量Epo、烘缸传给空气的能量比(散热比)Rao(%)，则出二次蒸汽流量Fso为：

Fso=FsiRso

(18)

Eao=EsiRao

(19)

(20)

依据式(15)和式(16)，所需进新鲜蒸汽的流量Fsi为：

(21)

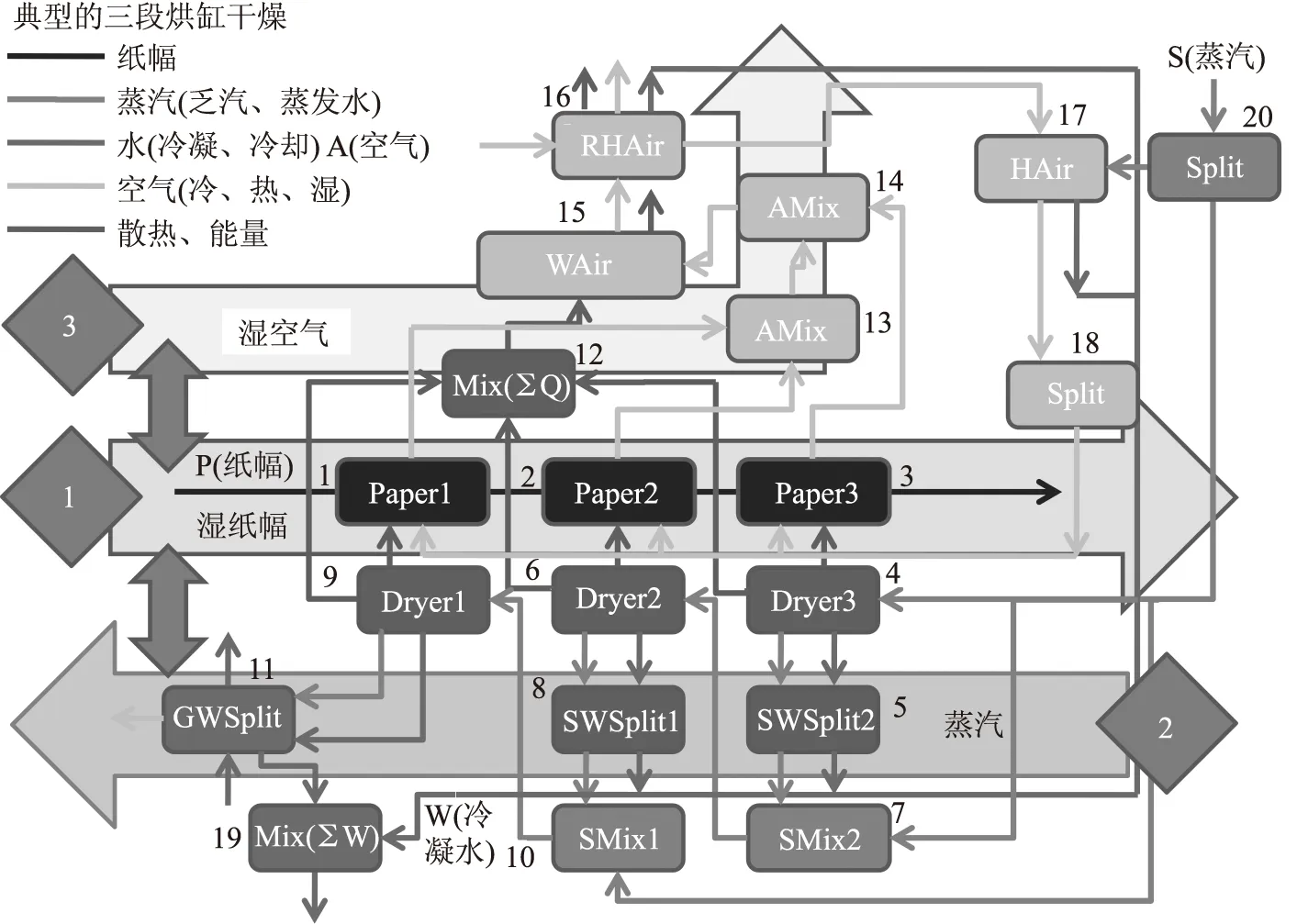
图3 典型三段烘缸干燥的模块流程图(考虑纸幅干燥速率)

图4 中山永发11#纸机前干燥的工艺流程

2 模块流程图

根据建立的干燥部各功能模块，针对典型的三段烘缸干燥过程，如果综合考虑纸幅干燥水分蒸发速率(蒸发水量)与蒸汽消耗、通风能耗(包括通风电耗)、蒸汽与空气的状态变量和主要设备变量等因素，可组建出如图3所示的模块流程图。

图3中菱形格内的数字表示大致的计算顺序，即先计算纸幅模块，然后再计算烘缸组和汽水分离器模块，最后计算气罩和通风系统等模块。模块旁边的数字表示具体的计算顺序。

模块流程图可通过仿真系统对具体纸机干燥部进行模拟。模拟结果与实际生产数据对比之后，利用各功能模块机理模型计算未知变量，并与实验或生产现场采集对应功能模块相应未知变量对比，来验证与修正各功能模块机理模型的参数，使机理模型与实际生产更吻合，以便最终建立与实际生产情况符合的纸机干燥部各功能模块的机理-实验模型和仿真系统。通过单元模型组合，应用功能模块可易于构建表征各种复杂的干燥过程的仿真系统。

3 应用案例

以中山永发纸业有限公司(简称“中山永发”)11#纸机的前干燥为例，探讨本研究提出的模块的应用。该厂11#纸机于2004年投产，主要生产定量为105～145 g/m2的高强瓦楞芯纸。整个干燥部采用半封闭式气罩，为无袋通风，分为前干燥和后干燥两部分。前干燥由48个直径为1.5 m的烘缸组成，共分为5组烘缸，四段通汽；后干燥由14个直径为1.8 m的烘缸组成，分2组，两段通汽。前干燥出来的纸幅经过施胶进入后干燥，从而得到高强瓦楞芯纸。图4为11#纸机前干燥的工艺流程。

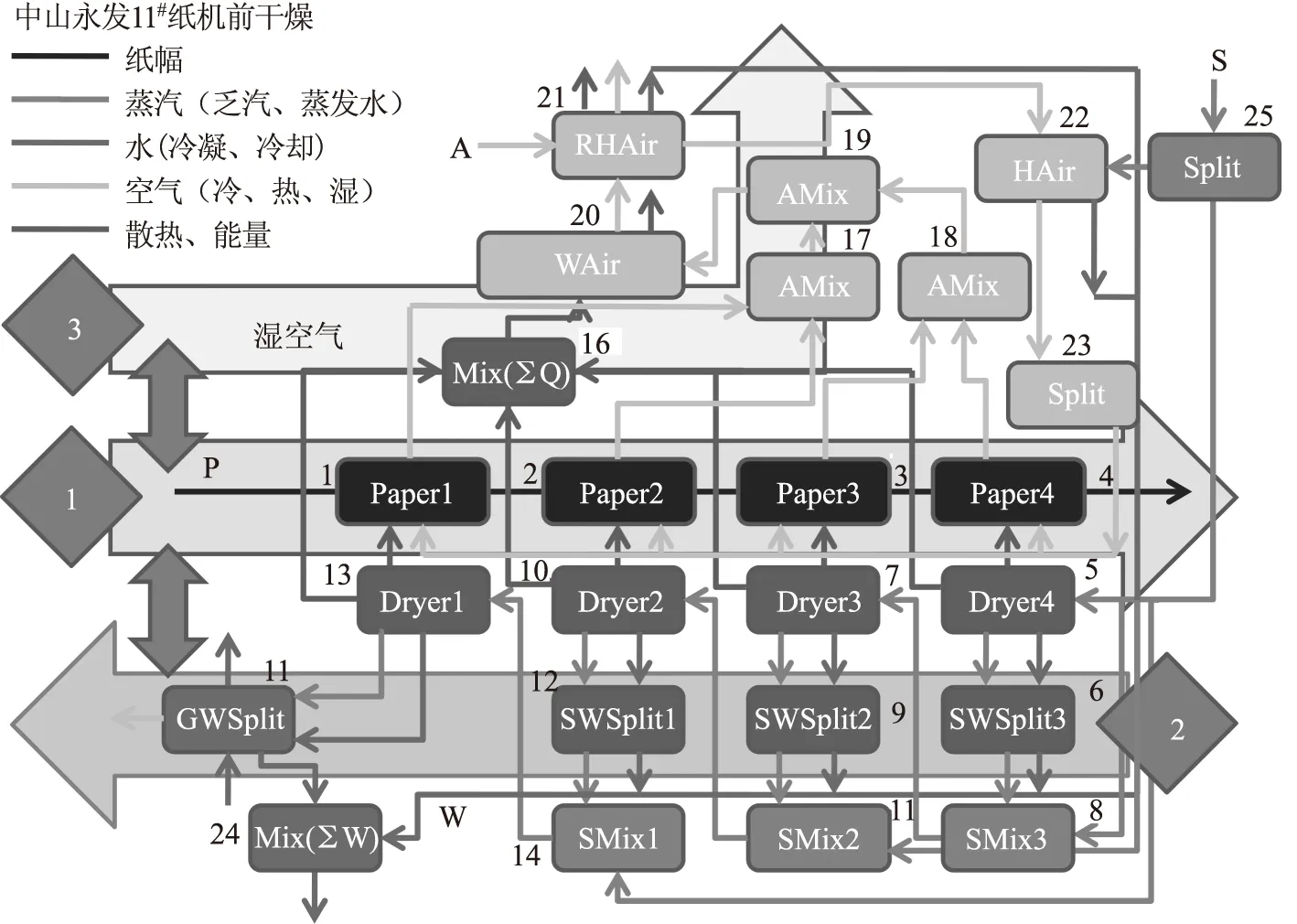
图5 中山永发11#纸机前干燥的模块流程图

图6 中山永发11#纸机前干燥的仿真流程

应用本研究提出的模块，中山永发11#纸机前干燥的模块流程图如图5所示。

在上述单元模型与功能模块的基础上，采用面向对象等技术开发了纸机干燥部仿真软件WinPAMS[28]。在WinPAMS中可以根据图4所示的11#纸机前干燥工艺流程以及图5所示的模块流程图，构造出如图6所示的11#纸机前干燥的仿真流程。WinPAMS采用序贯模块法，基于联立方程，结合物性库，通过迭代计算收敛等方法对仿真流程进行求解。

中山永发11#纸机前干燥主要工艺参数如表1所示。表2为仿真结果。

表2表明，用WinPAMS对11#纸机前干燥进行仿真，可以获得如下益处。

(1)根据前干燥的工艺流程(见图4)及其模块流程(见图5)，用可视化的方式可直接构造11#纸机前干燥的仿真流程(见图6)。

(3)在表1所示条件下，蒸汽消耗总量为12105.11 kg/h，即纸机前干燥的吨纸汽耗为1.25 t/t纸(12105.11/9713)，比改造前(由四段通汽改为三段通汽)实际的前干燥吨纸汽耗(约为1.3 t蒸汽/t纸)略低。产生这个现象的主要原因是在实际生产过程中，每个烘缸的接触和对流干燥速率是不同的，但在本应用中，将48个烘缸分为4个烘缸段，每个烘缸段的接触和对流干燥速率是相同的。另外，表2蒸汽流量的仿真结果表明，已解决了干燥部通入各烘缸段新鲜蒸汽量难以测量的问题。

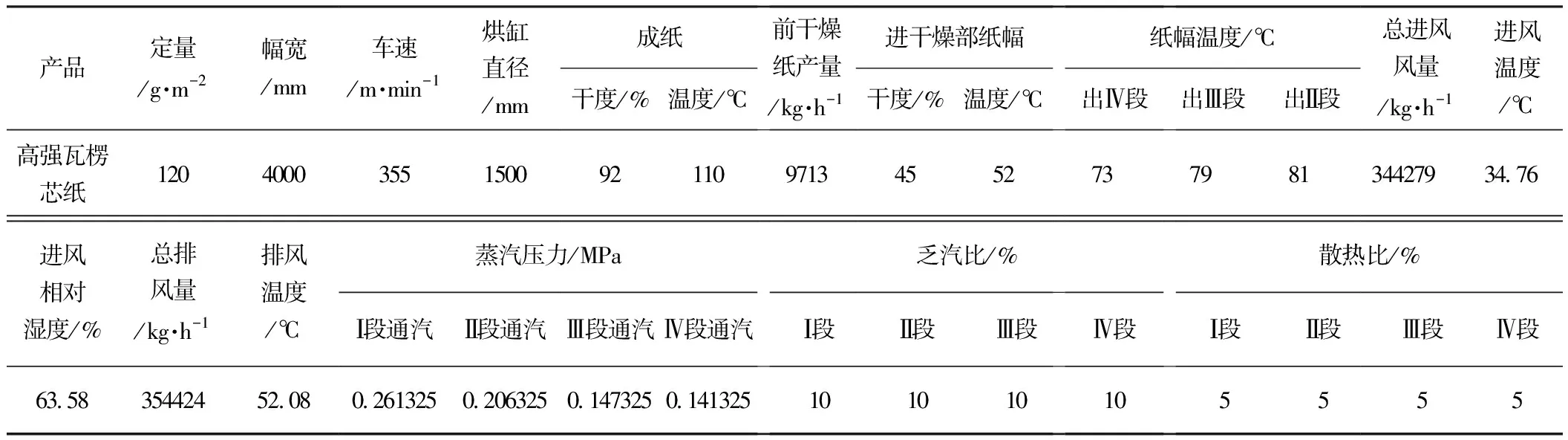
表1 中山永发11#纸机前干燥主要工艺参数

表2 仿真结果

(4)随着进湿纸幅温度的提高(由52℃提高到53℃)，蒸汽消耗总量降低。在保证成纸干度的前提下，蒸汽消耗总量为12078.43 kg/h，新鲜蒸汽节省26.58 kg/h。当然，提高进湿纸幅的温度也需要消耗能量，但仿真结果表明，本研究建立的模型基本合理。

(5)在保证成纸干度的前提下，如果Ⅳ段增加1个烘缸、Ⅰ段减少1个烘缸，蒸汽消耗总量为12087.66 kg/h，新鲜蒸汽节省17.45 kg/h。这说明该厂前干燥的通汽方式仍存在改进的空间，可考虑增加Ⅳ段烘缸个数、减少Ⅰ段烘缸个数，或者将四段通汽改成三段通汽，以降低前干燥的吨纸汽耗。事实上，本研究完成后该厂将前干燥原来的四段通汽改为三段通汽，每段烘缸个数分别为Ⅲ段8个(1#～8#缸)、Ⅱ段14个(9#～22#缸)、Ⅰ段26个(23#～48#缸)，改造后前干燥吨纸汽耗约为1.28 t/t纸，蒸汽消耗节省了1.54%。

(6)上述分析表明，中山永发的11#纸机通过将半封闭气罩改成封闭气罩、提高进湿纸幅温度或者干度、改变不同烘缸段的烘缸个数、改变进不同烘缸段新鲜蒸汽的压力或流量等手段，可节省新鲜蒸汽用量，降低吨纸汽耗。

(7)用WinPAMS对纸机干燥部进行仿真，可通过改变进烘缸纸幅温度、干度，改变烘缸分组，改变蒸汽操作参数(流量、压力/温度)，改变空气操作参数(通风量、温度、相对湿度)，改变通汽/气方式等手段来研究干燥部蒸汽消耗情况，为优化干燥部的设计及运行，提高干燥部的能效打下基础。

4 结 语

在此基础上，基于序贯模块法，应用功能模块构建了干燥部的模块流程图，并对中山永发11#纸机前干燥进行了仿真，仿真结果与实际测量结果基本一致。应用结果表明，通过提高进湿纸幅的温度或干度、改变进不同烘缸段新鲜蒸汽的压力或流量等手段，可提高湿纸幅干燥速率，节省新鲜蒸汽用量，降低吨纸汽耗。

参 考 文 献

[1] 国家发展与改革委员会, 工业和信息化部, 国家林业局. 造纸工业发展“十二五”规划[J]. 中华纸业, 2012, 33(1): 8.

[2] Worrell E, Price L, Neelis M, et al. World Best Practice Energy Intensity Values for Selected Industrial Sectors[R]. California: Ernest Orlando Lawrence Berkeley National Laboratory, 2008.

[3] Yaroslav C, Aleksander K, Lester S. Laboratory development of a high capacity gas-fired paper dryer[R]. Des Plaines(IL): Gas Technology Institute- Energy Utilization Center, 2004.

[4] 卢谦和. 造纸原理与工程 [M]. 2版. 北京: 中国轻工业出版社, 2007.

[5] Karlsson M, Oyg M. Papermaking science and technology series. Papermaking Part 2, Drying[M]. Finish Paper Engineers’ Association and TAPPI, 2000.

[6] Karlsson M, Stenström S. Static and dynamic modelling of cardboard drying [J]. Drying Technology, 2005, 23(1/2):143； 2005, 23(1/2):165.

[7] Nilsson L. Heat and mass transfer in multicylinder drying[J]. Chemical Engineering and Processing, 2004, 43(12):1547； 2004, 43(12): 1555.

[8] Yeo Y K, Hwang K S, Yi S C, et al. Modeling of the drying process in paper plants[J]. Korean Journal Chemical Engineering, 2004, 21(4): 761.

[9] Etemoglu A B, Can M, Avci A, et al. Theoretical study of combined heat and mass transfer process during paper drying [J]. Heat Mass Transfer, 2005, 41(5): 419.

[10] 周 强, 韩九强. 基于遗传算法的烘缸干燥曲线的参数优化[J]. 中国造纸学报， 2007, 22(1): 80.

[11] 沈胜强, 卢 涛, 李素芬. 纸页干燥过程计算模型[J]. 中国造纸, 2003, 22(4): 22.

[12] 沈胜强, 卢 涛, 李素芬. 纸页干燥过程的数值模拟与参数分析[J]. 中国造纸学报， 2003, 18(1): 119.

[13] Lu T, Shen S Q. Numerical and experimental investigation of paper drying: Heat and mass transfer with phase change in porous media[J]. Applied Thermal Engineering, 2007, 27(8/9): 1248.

[14] Kong L B, Liu H B. A static energy model of conventional paper drying for multicylinder paper machines[J]. Drying Technology, 2012, 30(3): 276.

[15] 林治作, 李继庚, 周艳明, 等. 双干网多烘缸纸机纸页干燥过程建模研究[J]. 造纸科学与技术, 2012, 31(3): 78.

[16] 刘金星, 刘焕彬, 高英莲. 制浆造纸工业过程仿真平台的研究[J]. 中国造纸学报, 2011, 26(1): 55.

[17] Bujak J. Energy savings and heat efficiency in the paper industry: A case study of a corrugated board machine[J]. Energy, 2008, 33(11): 1597.

[18] Roonprasang K. Thermal analysis of multi-cylinder drying section with variant geomretry[D]. Tagungsband: TU Dresen, 2008.

[19] Sivill L, Ahtila P, Taimisto M. Thermodynamic simulation of dryer section heat recovery in paper machines [J]. Applied Thermal Engineering, 2005， 25(8/9): 1273.

[20] Sivill L, Ahtila P. Energy efficiency improvement of dryer section heat recovery systems in paper machines-A case study [J]. Applied Thermal Engineering, 2009, 29(17/18): 3663.

[21] Kong L B, Liu H B, Li J G, et al. Waste heat integration of coating paper machine drying process[J]. Drying Technology, 2011, 29(4): 442.

[22] 李玉刚, 刘焕彬, 李继庚, 等. 基于联立模块法的造纸机干燥部操作参数优化[J]. 华南理工大学学报: 自然科学版, 2011, 39(3): 8.

[23] Li Y, Liu H, Li J, et al. Process parameters optimization for energy saving in paper machine dryer section[J]. Drying Technology, 2011, 29(8): 910.

[24] Koper G J M, Kjelstrup S, van de Ven T, et al. Entropy production for cylinder drying of linerboard and newsprint[J]. International Journal of Heat and Mass Transfer, 2007, 50(7/8): 1344.

[25] Zvolinschi A, Johannessen E, Kjelstrup S. The second-law optimal operation of a paper drying machine[J]. Chemical Engineering Science, 2006, 61(11): 3653.

[26] Gong M. Exergy analysis of a pulp and paper mill[J]. International Journal of Energy Research, 2005, 29(1): 79.