PID神经网络在卷纸辊张力控制中的应用

邓 肖 胡慕伊

(南京林业大学江苏省制浆造纸科学与技术重点实验室，江苏南京，210037)

在纸机运行过程中，卷纸辊张力是一个重要的参数[1]。张力太大会造成断纸，不仅影响生产，还会造成一定的经济损失；张力过小则会出现纸幅松弛现象，引起堆积和褶皱，对成纸质量产生影响。因此，控制好卷纸辊张力，不仅能有效提高生产效率，还能使纸机运行更加稳定，提高产品质量。在纸机卷曲过程中，卷纸辊张力控制是一个时变、强耦合、多干扰的非线性系统，中间环节有很多影响，且具有很多其他不可预测的因素，因此保持适宜的卷纸辊张力有很大难度。

PID神经网络(Proportional Integral Derivative Neural Network，PIDNN)是一种由比例元(P)、积分元(I)、微分元(D)组成的3层前向神经元网络。网络的输入层接受系统给的信号和对象输出信号，网络的隐含层(神经元个数、连接方式、连接权重初值)是按PID控制规律的基本原则确定，采用误差反向传播算法修改连接权重，通过在线训练和学习，改变网络中比例、积分、微分作用的强弱，输出层实现规律的综合。它具有传统PID控制器结构简单的优点，又具有神经网络的并行结构和本质学习记忆功能，以及多层网络逼近任意函数的能力[2]。本课题研究了PIDNN控制器对卷纸辊张力的控制，并与传统PID控制器控制效果进行比较。

1 卷纸辊张力控制系统模型

在纸张卷曲过程中，由于纸卷半径不断变化使得卷辊转动惯量、线速度等处于不断变化中，因此卷纸辊张力控制过程是一个时变的非线性系统[3]，纸机卷纸辊控制系统结构及纸张受力如图1所示。

图1 卷纸辊张力系统原理图

在卷纸机启动达到稳定后，其放卷线速度V1是恒定值，只有V2>V1，纸幅才能产生一定的张力使卷纸辊正常卷纸，卷纸辊卷绕速度V2=2πRn。由于纸张不断增加，R逐渐变大，张力F也会成比例增大，卷纸辊力矩M=FR将以更快速率增大，导致纸幅拉伸过度直至断纸。要使V2恒定不变，则转速n要减小，所以此系统是一个时变非线性系统。力矩M与张力F的传递函数的表达式为：

(1)

式中：K为常数；γ为阻尼系数；R为卷纸辊卷径(变化)。

磁粉离合器是电磁离合器的一种，它是靠线圈的通断电来控制离合器的结合和分离。磁粉离合器有主动件、从动件和固定支撑3部分组成；其工作原理是在主动件和从动件之间放置一定量的软性磁粉，励磁线圈不通电时，磁粉处于离散状态，励磁线圈通电吋，线圈中产生了电流，此时磁粉结合成磁粉链，从而主动件带动从动件转动，将转矩由输入端传给从动件，从动件即可驱动机器运转。励磁电流增大时，磁感应强度也增大，电磁吸力增大，传递的力矩就变大，反之，励磁电流减小，传递的力矩减小[4]。

磁粉离合器是根据电磁原理并利用磁粉来传达转矩的,其传达的转矩与励磁电流基本成线性关系，当励磁电流保持不变时,力矩不受传动件与从动件之间速度差(滑差转速)的影响,这是磁粉离合器的一大优点，只要励磁电流恒定,就可以稳定地传达恒定的力矩。因此，在造纸机卷纸辊张力控制中，只需调节励磁电流的大小，便能准确控制并传达所需力矩，从而准确控制卷纸辊张力。

磁粉离合器传递的力矩取决于励磁线圈中的电流,它们之间的关系可近似看作是一阶惯性环节[4-5]。但是,磁通产生后，磁粉由离散状态到形成磁粉链有一定的延时，所以磁粉离合器具有滞后的特性。磁粉离合器的传递函数为:

(2)

式中：M(s)为磁粉离合器力矩；IM(s)为励磁电流；Km为磁粉离合器增益；τ为磁粉离合器滞后时间；Tm为时间常数。

总的传递函数为：

(3)

2 PIDNN参数调整算法

2.1 PIDNN结构形式

张力控制系统只有一个控制量，本实验采用的是单输出的SPIDNN(Single-output PIDNN)。图2为SPIDNN控制器结构，其网络为2×3×1的结构，属3层前向神经元网络形式，包括输入层、隐含层和输出层。输入层有2个神经元，其输入分别为控制系统给定值r和被控对象输出值y；隐含层有3个神经元，分别为比例元、积分元和微分元，分别完成比例、积分和微分运算；输出层有1个神经元，完成控制规律的综合和输出[6]，PIDNN及其控制系统结构如图2所示。

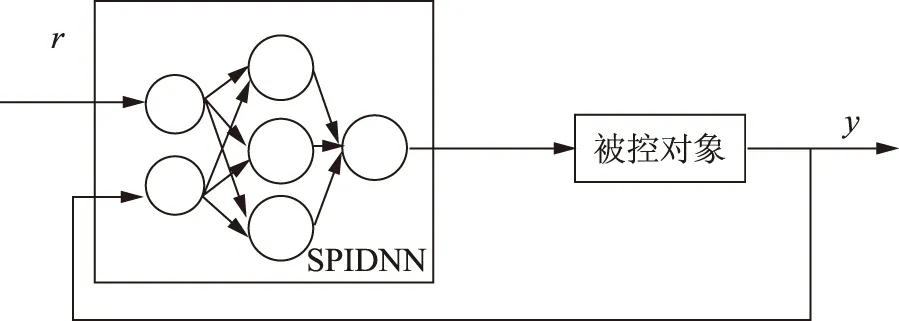
图2 SPIDNN及其控制系统结构

2.2 PIDNN的控制算法

PIDNN的算法由前向算法和误差反向传播算法两部分组成[2]。

2.2.1PIDNN的前向算法[7]

(1)输入层

PIDNN的输入层有2个神经元，在构成控制系统时可分别输入系统被调量的给定值r(k)和实际值y(k)。神经元的状态函数u(k)等于输入net(k),即：

ui(k)=neti(k)

(4)

输入层各神经元的输出函数均为比例阈值函数。

(2)隐含层

隐含层有3个神经元，分别为比例元、积分元和微分元，完成对应的比例、积分和微分计算。它们各自的输入均为输入层至隐含层的加权求和，即:

(5)

式中：wij是输入层第i个节点到隐含层第j个神经元的权重；上标“′”为隐含层标记。

比例元的状态为：u1′(k)=net1′(k)

(6)

积分元的状态为：u2′(k)=u2′(k-1)+net2′(k)

(7)

微分元的状态为：u3′(k)=net3′(k)-net3′(k-1)

(8)

(3)输出层

输出层结构比较简单，只有1个神经元，完成网络的总和输出功能，输入为隐含层到输出层的加权求和，即：

(9)

式中：xj′(k)为隐含层各神经元的输出值；wj′为隐含层到输出层的连接权值；上标“″”为输出层变量标记。

输出层神经元的状态函数

u″=net″(k)

(10)

PIDNN的输出就等于输出层神经元的输出。

2.2.2PIDNN的误差反向传播算法

PIDNN的误差反向传播算法完成网络权重的修改，即完成学习和记忆功能。PIDNN训练和学习的目的是使被控变量给定值和实际值的偏差最小，整个网络的控制目标和训练准则为：

(11)

按梯度法调节PIDNN权值，经n步训练和学习后，权值分别由以下各式确定。

输入层至隐含层的权值迭代公式为：

(12)

式中：ηij为wij的学习步长。

隐含层至输出层的权值迭代公式为：

(13)

式中：ηj为wj′的学习步长。

3 仿真实验

以江苏某纸厂一个典型造纸机的卷纸辊张力控制系统的模型为控制对象，带延迟的二阶模型为：

利用MATLAB/Simulink可以建立此仿真模型，根据经验并反复调试得到常规PID控制参数为KP=4.8、KI=0.006、kD=12.5。

根据PIDNN控制器的原理，在MATLAB中编程实现PIDNN控制单变量系统。下面给出反传算法代码：

disp([′反传算法开始:迭代次数：′,num2str(n),′/′,num2str(MaxNum)]);

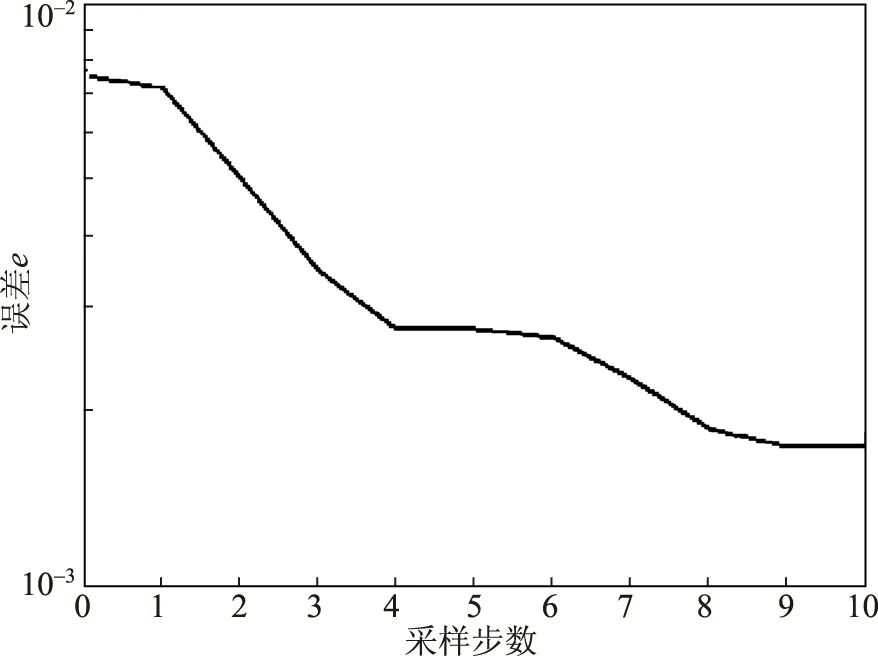
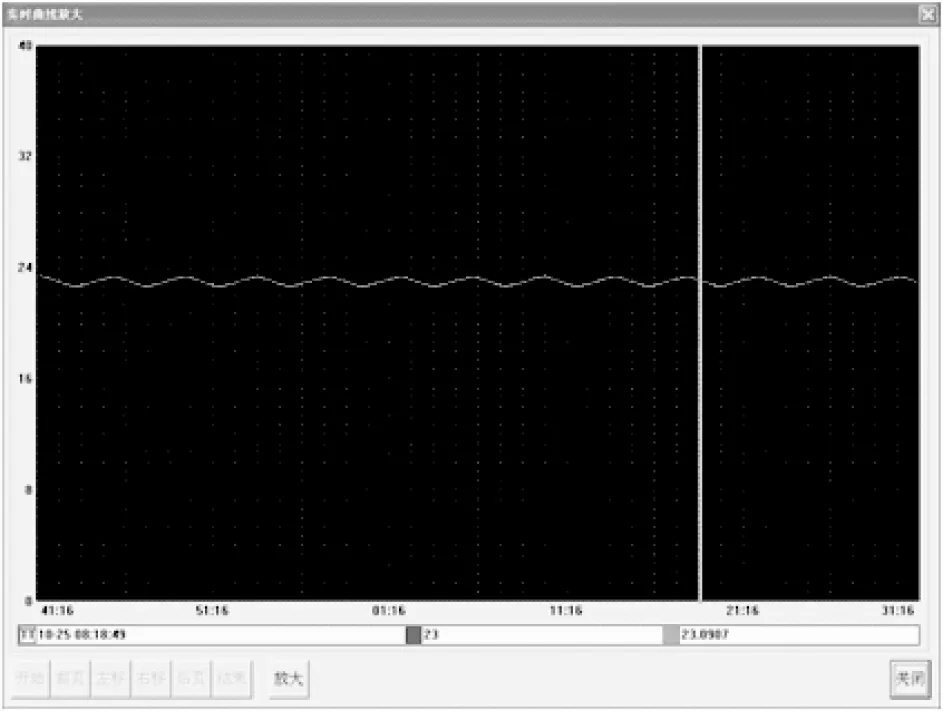
if Je(n)

disp(′反传算法break结束′);

break;

end

ifn==1‖(n>1&(Je(n)<=Je(n-1)))

disp(′权值改变为新值′);

forj=1:3

x1=0;

fork=2:m-1

x1=x1+e(k)*sign((Y(k+1)-Y(k))*(xo(k)-xo(k-1)))*xj(j,k);

end

dwj(j)=-x1/200;

end

PIDNN控制系统中，设网络的学习步长η=0.1，每步采样点数m=100,输入层至隐含层的连接权重初值w1j=1，w2j=-1，j=1,2,3；隐含层至输出层的连接权重初值wj′(0)取小于0.1的随机数。采样周期T=3。造纸机卷纸辊张力由阶跃信号给定。

从图3可以看出，通过常规调节PID控制参数，其控制并不理想，虽然输出没有超调，但调节时间超过15 s，不能满足卷曲过程的工艺要求；如果缩短调节时间，则会发生超调。PIDNN算法响应曲线无超调，无静差，响应速度快，调节时间为1 s左右，其控制性能明显优于常规PID控制器，对张力波动的反应更快、更准。

图3 常规PID和PIDNN仿真结果比较图

进入稳态以后，加20%干扰，PIDNN控制系统的输出曲线如图4所示。由图4可知，加入干扰后调节非常及时，表明此控制器具有较好的抗干扰能力。图5为PIDNN训练的前10步，网络的目标误差呈单调递减趋势并且衰减很快。

图4 干扰作用下PIDNN控制曲线

图5 网络训练曲线

图6 方波作用下网络跟踪曲线

给定系统输入采用方波函数：r(k)=1(k)-0.8(k-100)时，PIDNN控制系统的输出曲线如图6所示，系统的静态性能很好，表明PIDNN控制器具有良好的自适应性。

由上述结果可知，PIDNN控制器通过自学习和参数调整，使系统很快达到较好的动态和静态性能，系统的输出响应无超调、无静差、响应速度快、过渡时间短，收敛性好。

4 应用实验

PlD神经网络控制算法采用开发功能构件的方法,使用VB语言编写算法处理程序,生成包含MCGS工控机接口的ActiveDLL策略模块(PlDNN策略模块),供MCGS进行策略调用。其核心是从MCGS实时数据库取得网络参数和实时数据，对MCGS实时数据用VB进行算法运算和处理，随后送回MCGS，对被控对象进行控制，MCGS实际数据库对应于卷取段卷纸辊张力控制的实时数据，网络经过10步的在线训练，调节权值，最后实施控制。本课题将PIDNN用于MCGS工控机中，模拟对卷纸辊张力的控制。系统运行效果如图7所示。由图7可知，卷纸辊张力波动<1 N，达到了较好的控制效果。

图7 PIDNN在MCGS中对卷纸辊张力的控制曲线

5 结 语

在造纸过程中，纸机卷纸辊张力控制是一个时变、强耦合、多干扰的控制对象，传统的控制方法难以达到理想的控制效果；本实验采用PID神经网络(PIDNN)，不依赖控制对象的数学模型，将PID控制规律融入多层神经网络，采用误差反向传播算法修改连接权重，通过训练自主调整网络权值，改变网络中比例、积分和微分作用的强弱，使目标函数达到最优值。仿真结果及在MCGS工控机中的实验结果显示，PIDNN控制器对卷纸辊张力控制的效果较好。

参 考 文 献

[1] 黄俊勇. 复合机张力的模糊控制算法研究与应用[D]. 长沙： 中南大学， 2006.

[2] 舒怀林. PID神经网络及其控制系统[M]. 北京： 国防工业出版社, 2005.

[3] Hakan Koc, Dominique Knittel, Michel de Mathelin, et al. Modeling and Robust control of systems for elasticwebs[J]. IEEE Transactions on Control Systems Technology, 2002, 2(10): 197.

[4] 刘建建， 陈祝平. 磁粉离合器及其应用[J]. 机电技术， 2010(4): 63.

[5] 李 华， 姚 进， 赵世佳. 高效液力变矩传动系统[J]. 机械工程学报， 2010， 46(13): 116.

[6] 舒怀林. 基于PID神经网络的倒立摆控制系统[J]. 机床与液压， 2008， 36(3): 142.

[7] 翟饶杰， 舒怀林， 熊胜祖. PID神经网络改进研究[J]. 机电工程技术， 2010， 39(8): 39.