CCR模型“投影”有效的新证

彭 军 宋马林

(安徽财经大学统计与应用数学学院， 安徽 蚌埠 233030)

随着资源日益枯竭，人们对生产过程越来越重视。人们总是期望能够更加理性地去分析生产过程、投入冗余及产出亏损，其中生产效率是反映生产过程是否理想的一个很重要的指标，因此计算生产效率已成为一个热门的研究内容，其研究成果可以作为企业或者政府进行生产和管理的理论依据。这些理论成果有利于改进要素投入量和产品产出量，从而达到提高生产效率的目的。关于生产效率的研究，学者们作出了很多尝试，其中数据包络分析(Data Envelopment Analysis，DEA)[1]方法是一种比较好的测度生产效率的工具。在数据包络分析中，每个生产活动被视为一个决策单元(Decision-making unit, DMU)，不仅能够计算出每个DMU的效率值，还能提供每个DMU的改进方向。改进方向就涉及到“投影”和“投影”有限性概念。经典的数据包络分析模型以及派生出的模型都会涉及到“投影”和“投影”有效性，因此其在数据包络分析中占重要的位置。CCR模型作为数据包络分析(DEA)的第一个模型，它对数据包络分析的发展具有深远的影响。CCR模型的一些定义及性质可以平行推广到其他的模型中，如有效性定义、“投影”定理及Pareto-Koopmans有效等。本文仅从CCR模型“投影”有效性考虑，对“投影”有效性进行重新证明。

1 文献综述和知识储备

Charnes等人[1]首次提出数据包络分析，它将数据包络分析与数学、工程学、计算科学、管理学和经济学等多个学科联系在一起：

假设存在n个决策单元(DMU)，每个决策单元都有m项投入、s项产出，决策单元j用DMUj(1≤j≤n)表示，记：xj=(x1j,x2j,…，xmj)T表示DMUj的投入向量，其中xij为DMUj对第i种投入的投入量，xij>0；yj=(y1j,y2j,…，ysj)T表示DMUj的产出向量，其中yrj为DMUj对第r种产出的产出量，yrj>0；对于被评价决策单元DMUj0用DMU0表示。基于相对有效概念，提出了决策单元DMU0相对效率的分式规划模型(1)：

uk≥0,k=1,2,…,s

vi≥0,i=1,2,…,m

(1)

式中：v=(v1,v2,…,vm)T、u=(u1,u2,…,us)T— 分别表示m项投入对应的权重向量和s项产出对应的权重向量。

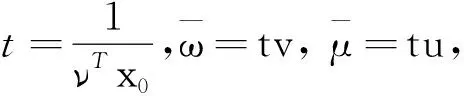
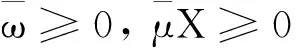
(2)

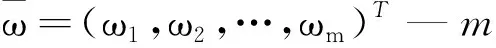
再利用对偶理论得到其对偶规划模型(3)：

minθ

λj≥0, j=1,2,…,n

S-≥0,S+≥0

(3)

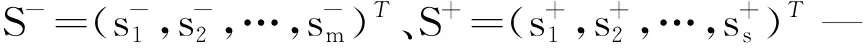
分式规划模型、线性规划模型和对偶规划模型统称为CCR模型。其中模型(1)和模型(2)的权重是选择最有利于决策单元DMU的相对效率评价的权重。对于模型(3)，定义了决策单元DMU(decision making units)相对有效，得到了决策单元DMU0相对有效的条件,即

并且提出相对有效和Pareto-Koopmans有效[4]的关系，即DMU0为DEA有效的条件可能也是Pareto-Koopmans有效的条件。这种方法契合了生产函数(production function)定义的要求，他们认为可以得到一种新的生产函数，这种生产函数有以下几个优点：(1)这种生产函数是从被评价决策单元得到的，没有具体的函数形式,因此这种生产函数可以直接应用于观测对象；(2)其他类型生产函数具有不易处理的缺点，这种生产函数能够避免这类缺点；(3)它还可以用于比较静态分析去检测生产技术是否发生变化。这个静态分析可以通过多种途径进行实现，比如在不同时期，当技术发生变化时，同一个决策单元应该被看作不同的主体。(4)这种方法不需要事先确定权重就可以得到DEA有效的决策单元，有利于减少主观因素导致的效率测量误差。DEA有效的决策单元构成了生产可能面。因此这些优点决定了数据包络分析方法具有很广泛的使用性，比如在企业管理、生产活动和银行等领域。他们还讨论了数据包络分析与非DEA有效决策单元“投影”[5]、等产量线分析、Farrell效率[6]、Shephard距离函数、成本函数和边际替代率之间的联系。Banker 等人[7]提出考虑规模收益变化的BCC模型，他们也研究了“投影”有效性。Charnes 等人[8]再次研究了CCR模型的决策单元DMU在有效面上的“投影”，他们还提出了CCGSS模型，分析了决策单元Pareto-Koopman有效与CCGSS模型的目标函数之间的关系，并且形象地描述了Pareto-Koopman有效的几何意义；在CCGSS模型下，他们还提出对非DEA有效的DMU“投影”的改进方法。Tone[9]提出了SBM(slack-based measure)模型,他探讨了SBM模型和CCR模型的关系，并且分析了SBM模型的“投影”问题。关于“投影”有效性，本文在前人的基础上提出2种新的证明方法，去解决其他模型“投影”有效定理，比如BBC模型，CCGSS模型，SBM模型等。

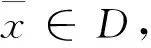
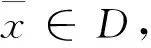
对于基于输入的CCR模型，假设生产可能集满足以下5条公理：(1)平凡性公理；(2)凸性公理；(3)锥性公理；(4)无效性公理；(5)最小性公理。由这5条公理可以推导出CCR模型的生产可能集TCCR：

λj≥0, j=1,2,…,n}

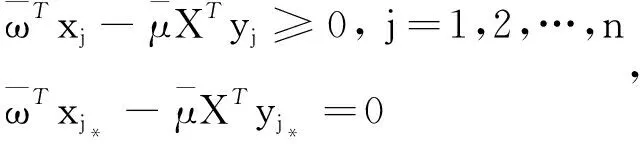
x*,yj*=y*

则 (Ⅰ)(x*，y*)是下列多目标规划的最优解

(VP1)min(x1j,x2j,…,xsj,-y1s,-y2s,…,-yms)

s.t. (x,y)∈TCCR，

其中，(x1j,x2j,…,xsj,-y1j,-y2j,…,-ymj)=(xj,-yj)

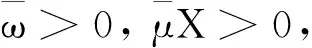
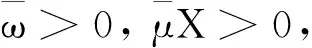
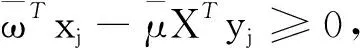
(Ⅱ)由(Ⅲ)知(x*，y*)是多目标规划(VP1)模型的最优解，多目标规划(VP1)模型可以转化为线性加权和问题[11]：

s.t. (x,y)∈TCCR

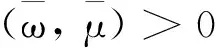
(Ⅲ)由(Ⅱ)得到(x*，y*)为多目标规划(VP1)的(弱)Pareto-Koopmans有效，又对于CCR模型，(弱)Pareto-Koopmans有效和(弱)DEA有效是等价的[12]，当(x*，y*)是(VP1)的弱Pareto-Koopmans有效解，则DMU*是弱DEA有效；当(x*，y*)为(VP1)的Pareto-Koopmans有效解，则DMU*是DEA有效。证毕。

3 新证法及推广

为了证明“投影”有效性，引进CCR模型“投影”的定义。

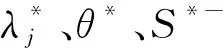
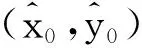
模型(2)和(3)分别引进非阿基米德无穷小ε，得到基于输入的CCR模型：

s.t. ωTxj-μTyj≥0, j=1,2,…,n

ωTx0=1

ωT≥εeT, μT≥εeT

(4)

minθ-εeTS+-εeTS-

λj≥0, j=1,2,…,n

S-≥0, S+≥0

(5)

其中eT=(1,1,…,1)

下面用新方法证明决策单元DMU0“投影”为DEA有效。

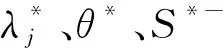
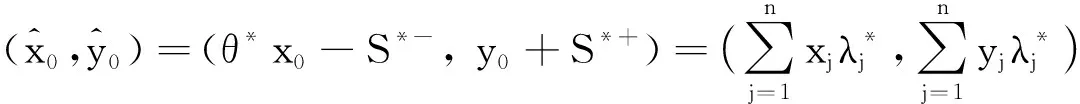
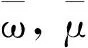
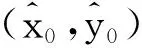
又由

(6)

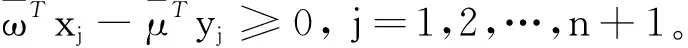
所以

(7)

由线性松紧定理得

(8)

(9)

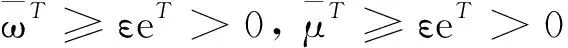
(10)

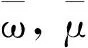
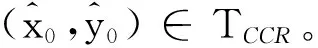
(11)

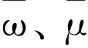
用新方法对BCC模型的“投影”有效进行证明。对于基于输入的BBC模型，规模收益是可变的，一般假设生产可能集满足以下4条公理：(1)平凡性公理；(2)凸性公理；(3)无效性公理；(4)最小性公理。由这4条公理可以推导出基于输入的BCC模型的生产可能集TBCC：

类似引理1，得到引理2：

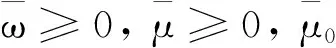
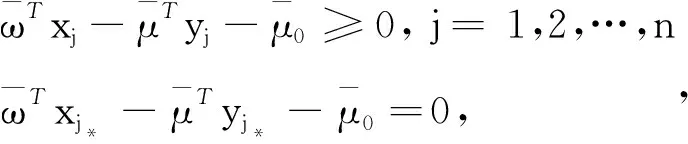
x*,yj*=y*

则 (Ⅰ)(x*，y*)是下列多目标规划的最优解：

(VP2)min(x1j,x2j,…,xsj,-y1j,-y2j,…,-ymj)

s.t. (x,y)∈TBCC

其中，(x1j,x2j,…,xsj,-y1j,-y2j,…,-ymj)=(xj,-yj)

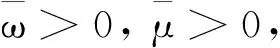
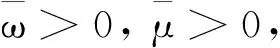
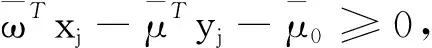
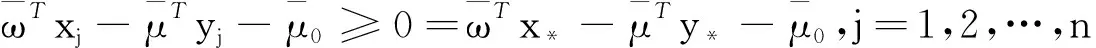
满足最优解的定义，得到(x*， y*)是多目标规划(VP2)的最优解。

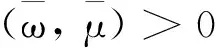
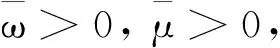
对于其他模型，如CCGSS模型，SBM模型，我们仍然可以应用类似的方法进行证明，本文不再详述。

4 结 论

数据包络分析是数学、计算科学、计算机科学、管理科学、经济学和工程学的一个交叉研究领域。数学证明能够使数据包络分析在逻辑上更加缜密，并且能使数据包络分析的一些经典模型的相关性质和定理相互联系在一起，比如CCR模型效率值和BCC模型效率值的大小关系、基于投入的CCR模型效率值和基于产出的CCR模型的效率值之间的关系、SBM模型与CCR模型之间的关系等。在研究过程中，学者们应该运用数学手段去分析新模型，找出模型之间的关系，并且能够运用已有的知识进行证明。

[1] Charnes A,Cooper W W,Rhodes E.Measuring the Efficiency of Decision Making Units[J].European Journal of Operational Research,1978,2(6):429-444.

[2] Charnes A,Cooper W W.Programming with Linear Fractional Functionals [J].Naval Research Logistics Quarterly 9,1962：3,4.

[3] Charnes A,Cooper W W,Wei Q L.A Semi-infinite Multicriteria Programming Approach to Data Envelopment Analysis with Many Decision-making Units [J].Center for Cybernetic Studies Report,CCS, 1986,9:551 .

[4] Charnes A,Cooper W W.Management Models and Industrial Applications of Linear Programming [M].New York:Wiley,1961.

[5] Charnes A, Cooper W W, Rhodes E.Evaluating Program and Managerial Efftciency:An Application of Data Envelopment Analysis to Program Follow Through[J].Management Science,1981,27:668-687.

[6] Farrell M J.The Measurement of Productive Efficiency[J].Journal of Royal Statistical Society A,1957,120:253-281.

[7] Banker R D, Charnes A,Cooper W W .Some Models for Estimating Technical and Scale Inefficiencies in Data Envelopment Analysis [J].Management Science,1984,9:1078-1092.

[8] Charnes A, Cooper W W, Golany B, et al.J Foundations of Data Envelopment Analysis for Pareto-Koopmans Efficient Empirical Production Function [J].Journal of Econometrics, 1985,30:91-107.

[9] Tone K.A Slacks-based Measure of Efficiency in Data Envelopment Analysis[J].European Journal of Operational Research,2001,130(3):498-509.

[10] 魏权龄.数据包络分析[M].北京:科学出版社,2004:27.

[11] 魏权龄.评价相对有效的数据包络分析模型[M].北京：中国人民大学出版社,2012:47- 48.

[12] 盛昭瀚,朱乔,吴广谋.DEA理论、方法和应用[M].北京：科学出版社,1996:49-57.

[13] 魏权龄.评价相对有效的数据包络分析模型[M].北京：中国人民大学出版社,2012:115-116.