油料装备故障检测数据融合研究

曾慧娥 周庆忠 胡为艳

(1.重庆科技学院机械与动力工程学院， 重庆 401331； 2.后勤工程学院， 重庆 401331；3.78088部队， 重庆 400039)

油料装备效能由运行状态监控、故障诊断、维修决策等环节及其相关技术来保证。油料装备运行环境呈动态分布式，使得油料装备运行状态监控难度大，检测数据繁多，故障诊断复杂，维修任务及其维修决策随机多变。如何充分利用油料装备信息资源，实现油料装备故障检测数据融合，是确保油料装备性能可靠迫切需要解决的问题[1]。针对这一问题，对油料装备故障检测数据融合进行研究，根据油料装备故障检测融合结果做出故障诊断决策，探讨提高油料装备运行状态评估及故障诊断性能的方法，对于提高油料装备效能具有重要作用。

1 油料装备状态检测数据融合

在线监测油料装备运行工况参数(如温度、压力、流量、振动等)，获取装备状态变化的预警参数。针对所采集的数据存在不确定性和模糊性，运用数据融合技术，利用多传感器数据间互补信息，消除检测数据误差和冗余信息，得到精度较高的关于装备零部件的工作性能、机械强度、疲劳极限与磨损程度等方面的数据融合结果[2-3]。

采用物理冗余和解析性冗余对传感器进行验证。物理冗余即是在相同空间位置使用多传感器，利用多数规则加权系统来确定实际读数，但它并不是在所有情况下都可行。而解析性冗余利用的是系统组件之间的功能关系。通常功能被独立于密切相关的子系统，以降低其复杂性。人工神经网络(Artificial Neural Networks, ANNs)具有进行非线性主成分分析的能力，主成分分析允许提取高维非线性数据集的主要特征，已被应用于传感器验证[4]。

油料装备状态检测数据融合模型如图1所示。采用三步训练法用于传感器验证和ANNs。第一步训练，采用来自专家系统的装备历史运行数据，组成神经网络的训练和测试样本，训练ANN权值和阈值，调整网络结构，测试其性能。第二步训练，将正常运行数据提供给ANN，ANN输出正常运行数据，以便学习ANN两者间功能关系。第三步训练，将包含异常运行数据的实际检测数据提供给ANN，由ANN按规则进行处理，输出正常运行数据。经过三步训练法，使ANN对检测数据变得“不敏感”，仅从数据集中提取适当特征参数，如振动、转速、温度、压力、流量、电压和噪音等，经过多传感器数据融合，推理出运行状态预测评估结果，并储存在动态数据库中。

ANNs可预测有故障传感器输出值的能力。如果用在关键油料装备保障任务场景下，即使检测到故障，也能提供所需信息来继续测试。这些估计数据还可向故障诊断算法提供精确数据，有助于确定油料装备系统失效源。

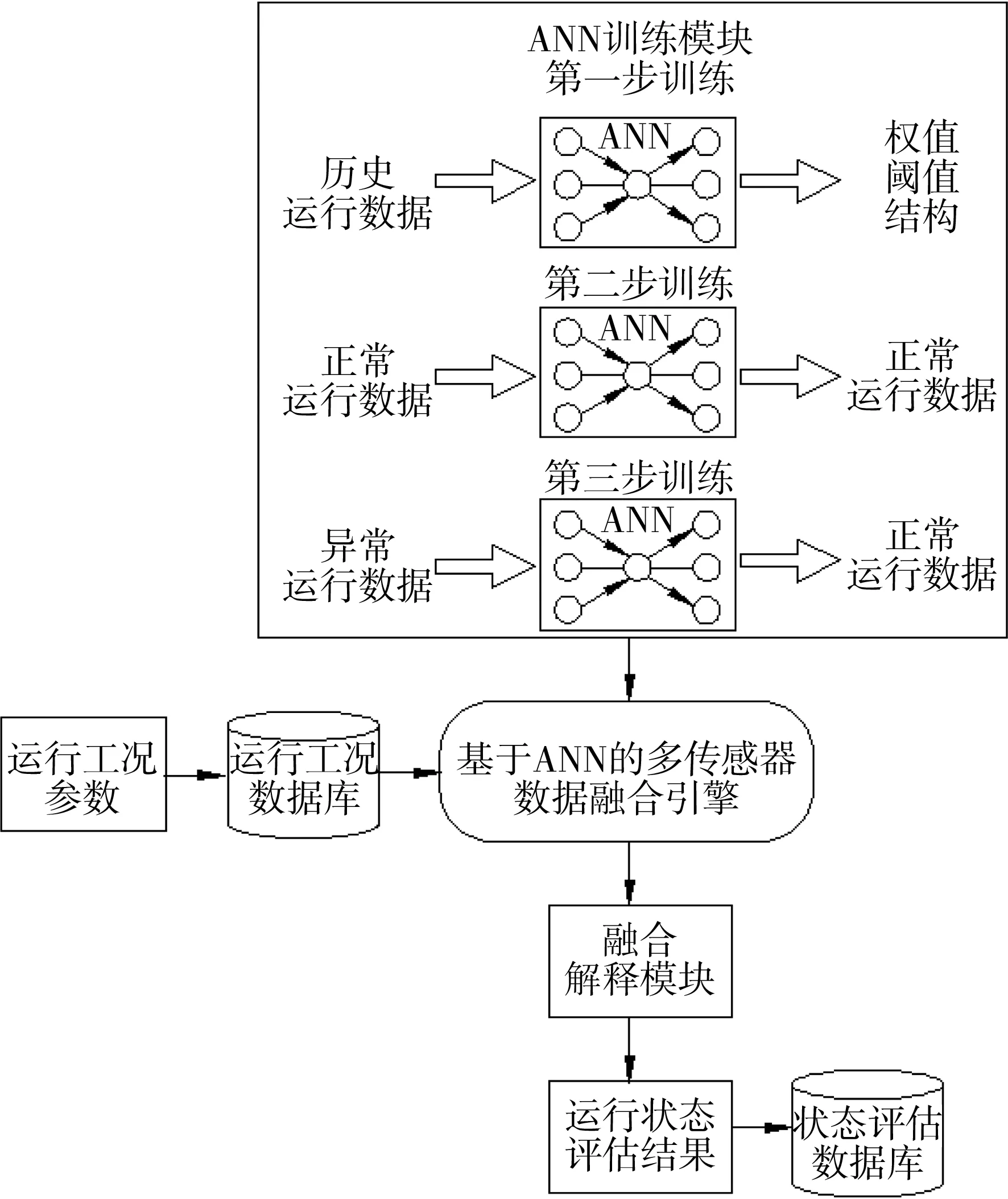
图1 油料装备状态检测数据融合模型

2 油料装备故障诊断数据融合

油料装备故障诊断数据融合过程如图2所示。

(1)数据压缩。由于油料装备故障检测数据变量及其数量庞大，传统存储方法难以维持。本文使用基于MPLS(Multiway partial least squares)的数据压缩技术，将由现场数据组成的高维数据集，投射到低维空间，由3D数据转换成2D矩阵排列。减少关于故障信息重要结构的高维数据空间，对高维数据集提供有效计算，减少输入维度和输出空间，寻找高度相关的潜变量。

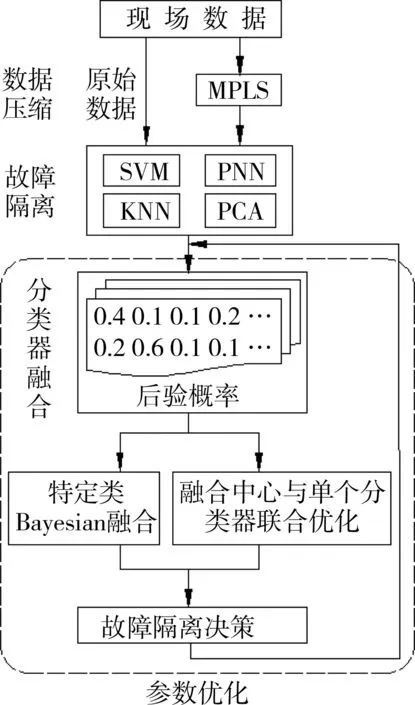
图2 油料装备故障诊断数据融合过程

(2)故障隔离。应用模式识别技术，如支持向量机(Support vector machine, SVM)、概率神经网络(Probabilistic neural network, PNN)、k近邻法(k-nearest neighbor, KNN)，使用多元统计方法，如主成分分析(Principal components analysis, PCA)，作为单个分类器进行故障隔离。

SVM使用内核函数拟合非线性可分离模型，采用径向基函数将数据转换到高维特征空间，寻找最大限度地提高类之间幅度的最优超平面。PNN监督估计每类概率分布函数，根据这些函数估计输入向量成为学习类别或类的可能性。使用先验概率对学习模式进行加权处理，确定给定输入矢量的类别。KNN分类器作为非参数分类方法，使用相对于给定指标d，最接近输入向量x的k-特征向量子集，完成输入向量x的分类。输入向量x则被分配给第k子集内最频繁出现的类。通过对k的选择，打破关联。PCA将相关变量变换为较小数量的互不相关的变量，计算训练数据的协方差矩阵、相应特征值和特征向量。对特征值进行排序，选择具有最高值的向量来表示较小维空间内数据。通过交叉验证确定主成分数目[5-6]。

(3)分类器融合。使用后验概率实施特定类Bayesian融合，实现融合中心与单个分类器的联合优化。根据融合结果，做出故障隔离决策，进行参数优化。

①特定类Bayesian融合

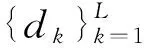
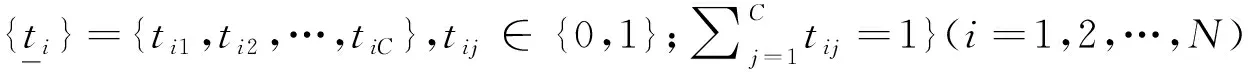
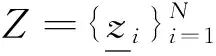
(1)

②融合中心与单个分类器的联合优化

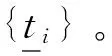
P(u1,u2,…,uL|cj)≈

(2)

通过每个分类器只与来自于训练数据的相对最好分类器进行关联，来简化概率计算。关键是联结耦合融合中心与单个分类器的决策规则，由于融合规则和其他分类器的决策策略是固定的，则第k个分类器做出的有关决策为：

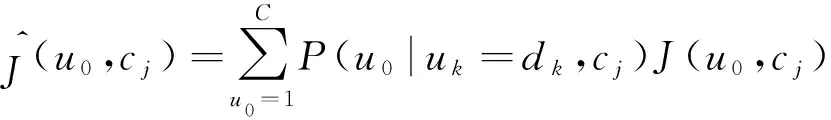
(3)

当本地分类器k做出决策dk，在先前迭代融合规则中，真实类是cj时，通过计算融合中心做出决策u0的一小部分时间，由训练数据计算P(u0|uk=dk,cj)。

3 多分类器动态融合

动态融合用在动态多故障诊断(Dynamic multiple fault diagnosis, DMFD)问题域，其目标是根据随着时间变化所观察到的测试分类结果(包括在油料装备系统中一组可能出现的故障状态和在各时间段所观察到的一组二元分类结果)，隔离多个故障。动态融合过程随着时间推移来计算最有可能优化序列，其实质即是在阶乘隐Markov模型(Hidden Markov model, HMM)中寻找最大后验概率配置[7]，如图3所示。

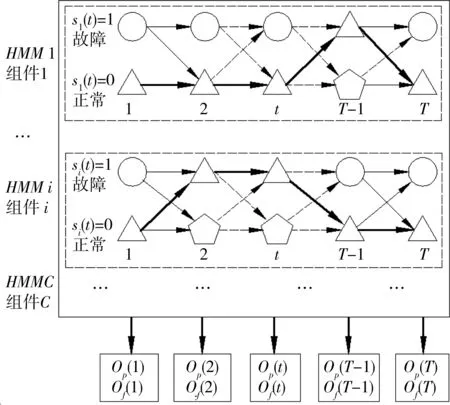
图3 基于阶乘HMM的动态融合处理

故障状态独立演变，组件状态之间不存在直接联系。每个分类器结果提供关于故障状态的一个子集信息。通过分类器结果联结组件状态。在各采样时间段，分类器结果的一个子集是可用的。在这个意义上，分类器并不完善。某些分类器结果失效，分类器存在与其相关的误检测和误报警概率。

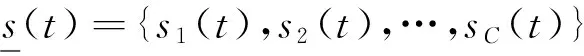
假设已知初始状态的概率分布。在各时间段的观测值是分类器的二元结果子集O={O1,O2,…,OL}，即On(t)∈{pass,fail}={0,1}。设已通过的分类器结果集为Op，失效的分类器结果集为Of。用si(t)表示在离散时序t，第i个HMM的隐蔽系统故障状态。每个故障状态si(t)被建模为一个两状态的HMM。在此，组件和分类器的真实状态被隐蔽。

用L将错误更正码(Error-correcting code,ECC)矩阵ECC=[emn]定义为规模为C的诊断矩阵(D-矩阵)，它表示故障源和分类器之间的全阶依赖。对于每个组件状态，即对于时刻t的组件si，A= {Pai(t),Pvi(t)}表示一组故障出现概率Pai(t)和故障消失概率Pvi(t)，分别被定义为Pai(t)=P(si(t)=1|si(t-1)=0)和Pvi(t)=P(si(t)=0|si(t-1)=1)。对于静态类，Pai(t)=Pvi(t)=0。当这些概率为非零时，HMM提供处理间歇性故障的能力。在此，D={d1,d2,…,dL}是L个可用二元分类器的有限集，对应于ECC矩阵的L列，用于确定系统完整性。参数集P={Pdn,Pfn}表示与每个分类器n相关的一对检测和误报警概率：

Pdn=P(On(t)=1|dn(t)=1)

Pfn=P(On(t) =1|dn(t)=0)

(4)

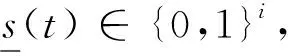
(5)

采用基于Lagrangian松弛和Viterbi解码的近最优多项式时间算法求解之。动态融合算法作为多故障诊断算法，存在分类失误与虚假故障失误的可能，采用以下指标对其性能进行评估。

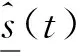
对所有时刻，失误分类率为：

(6)

平均失误分类率为：

(7)

虚假故障分类率FC是当时刻t处于故障状态时，由算法错误诊断的故障状态百分比为：

(8)

平均虚假故障分类率为：

(9)

在单一故障假设下，以较高失误分类率MC为代价来使虚假故障分类率FC等于零。

4 结 论

本文从油料装备运行状态检测、故障分析与诊断等方面，研究了油料装备故障检测数据融合问题：(1)应用ANNs实现油料装备状态检测数据融合，采用三步训练法用于传感器验证。(2)在故障诊断数据融合过程中，使用MPLS技术压缩数据，将模式识别技术和多元统计方法作为故障隔离的单个分类器。使用后验概率，进行特定类Bayesian融合，实现融合中心与单个分类器的联合优化，做出故障隔离决策，进行参数优化。(3)将动态多故障诊断问题域建模为阶乘隐Markov模型，通过寻找最大后验配置，实现多分类器动态融合。应用结果表明，故障检测数据融合降低了油料装备故障整体诊断误差，对于提高诊断性能，强化油料装备保障效能具有重要作用。

[1] 周庆忠，曾慧娥.油料装备维修管理信息化研究[J].中国管理信息化,2010(15):70-71.

[2] 曾慧娥，周庆忠.油料装备智能维修仿真平台研究[J].计算机仿真,2010,27(5):149-152.

[3] 周庆忠.油料装备勤务[M].北京:解放军出版社，2010.

[4] Ghate V N,Dudul S V.Cascade Neural-Network-Based Fault Classifier for Three-Phase Induction Motor [J].IEEE Trans.Industrial Electronics,2011,58(5):1555-1563.

[5] Ruta D,Gabrys B.An Overview of Classifier Fusion Methods [J].Comput.Inf.Syst.,2000,7(1):1-10.

[6] Stiller C,Puente Leon F,Kruse M.Information Fusion for Automotive Applications [J].Information Fusion，2011,12(4):244-252.

[7] Dhople S V,Dominguez-Garcia A D.A Parametric Uncertainty Analysis Method for Markov Reliability and Reward Models [J].IEEE Trans.Reliability，2012，61(3):634-648.