根据两颗导航星信息估计捷联惯导系统误差的一种方法

杨雪霖 张 英

1. 北京航天控制仪器研究所， 北京 100039 2. 北京航天自动控制研究所， 北京 100854



根据两颗导航星信息估计捷联惯导系统误差的一种方法

杨雪霖1张 英2

1. 北京航天控制仪器研究所， 北京 100039 2. 北京航天自动控制研究所， 北京 100854

针对高机动短时间飞行的飞行器，介绍了一种根据它相对2颗导航卫星的伪距离和伪速度信息，估计捷联惯导系统定位和定速度误差的方法。考虑到由确定飞行器相对每颗星的径向距离和速度的非线性方程施加的约束，根据这些误差矢量长度最小值的条件确定误差值。用空间解析几何法得出了计算捷联惯导系统误差估值的最终算法，这种算法能给出非线性最小值问题的精确解。

导航卫星； 捷联惯导系统； 误差；估计； 解析几何

由捷联惯导系统和卫星导航系统组成的组合式导航系统在飞行器控制系统中得到了广泛应用，通常用卫星导航系统来校对捷联惯导系统[1-2]。为了根据卫星导航系统的数据确定飞行器的坐标和速度，必须同时至少能测量4颗导航卫星[3]，才能保证计算和修正捷联惯导系统的误差。但是，这一条件在飞行器飞行过程中并不是都能满足。在导航系统工作时间较短时，观测到4颗星的限制条件比较明显，但观测到2颗导航星的概率却较高。

在可实现的集成式导航系统中，当可测量的导航星数量少于4颗时，可以用卡尔曼滤波算法或者附加传感器的信息来计算捷联惯导系统的误差。对工作时间较长的运动体，卡尔曼滤波的有效性较高，但是在较短的时间区间内，即使能观测到充分数量的导航星，统计算法的误差也可能会很大。对于工作时间较短的高度动态飞行器，在可观测的导航卫星数量少并且没有附加传感器的条件下，研究捷联惯导系统误差估计的算法是现实迫切的问题[4]。

为了确定飞行器的3个坐标和3个速度分量，至少必须有6个导航方程。当只能观测到2颗星时，只有4个导航方程。可以根据捷联惯导系统误差矢量的模的最小值条件得出缺少的2个方程。在这种情况下通常用变分法求解条件极值问题。对问题的分析表明，从几何表达的观点出发能较容易得到解。本文将介绍推导根据2颗导航星信息估计捷联惯导系统误差的方法[5]，文中使用地心直角坐标系。

1 捷联惯导系统确定坐标的误差估计

两颗导航卫星给出的飞行器可能的位置处于某个圆周上，如图1所示。该圆周的中心S0(x0,y0,z0)位于这2颗卫星的连线上，距第1颗卫星的距离是s1，圆周的半径是R0，圆周所在的平面与连接2颗卫星的直线垂直。

设飞行器上卫星导航接收机测量得到的到第1颗星和第2颗星的距离分别是D1,D2，则有

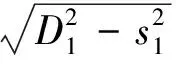
(1)

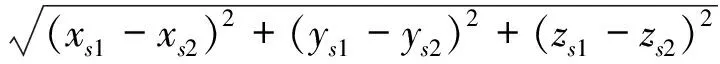
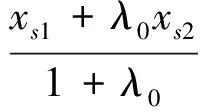
(2)

根据图1中所示几何关系，有

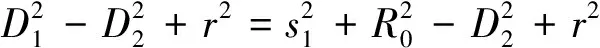
于是

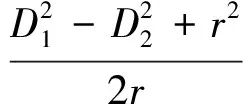
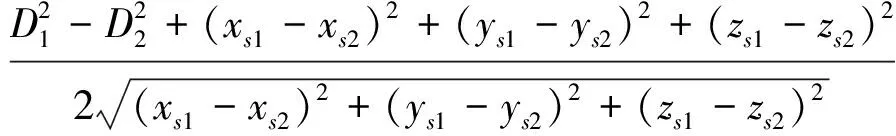
图1 根据观测2颗卫星确定捷联惯导系统的定位误差

在该圆周平面上求出与捷联惯导系统所确定的飞行器位置点G(xg,yg,zg)最接近的点P(xp,yp,zp)。设Ap=xs2-xs1，Bp=ys2-ys1，Cp=zs2-zs1，Dp=-Apx0-Bpy0-Cpz0是确定圆周所在平面的参数，其中平面的法线矢量是(xs2-xs1，ys2-ys1，zs2-zs1)，从点G(xg,yg,zg)到圆周所在平面的距离按下面的公式计算[6]

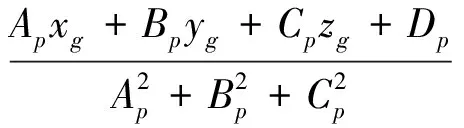
(3)

经过圆周中心点S0(x0,y0,z0)和点P(xp,yp,zp)的连线与圆周的交点是与捷联惯导系统所定出飞行器位置点最接近的点，计算该点的估值，就能得到飞行器的实际位置坐标估值：

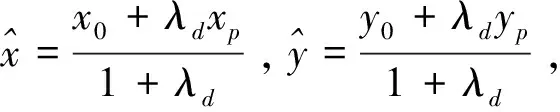
(4)

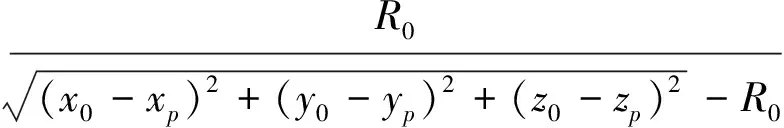
如果

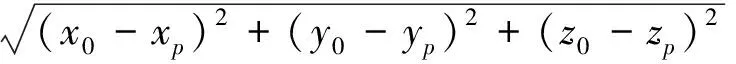
(5)

捷联惯导系统确定飞行器位置时出现的误差是

(6)

2 捷联惯导系统确定速度时的误差估计

设飞行器相对第i颗导航卫星的径向速度矢量的分量是xVi,yVi,zVi，如图2所示。

图2 可观测2颗卫星时确定捷联惯导系统速度误差示意图

利用直线的参数方程确定这些分量：

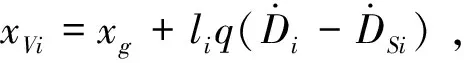
(7)

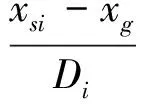
度分量，由卫星运动决定。

把相对第i颗卫星的测量值作为一些点的几何位置，这些点确定飞行器速度矢量的真正方向，该测量值给出一个平面，它经过点Vi(xVi,yVi,zVi)，并且与连接飞行器和卫星的直线垂直，该平面的方程如下：

lixp+miyp+nizp+Qi=0

(8)

两个平面P1和P2的法线矢量分别是{l1,m1,n1}和{l2,m2,n2}，式(8)表示这2个平面的交线，用下面的直线参数方程描述

xpp=x0V+lps，ypp=y0V+mps，
zpp=z0V+nps

(9)

式中，lp=m1n2-m2n1，mp=n1l2-n2l1，np=l1m2-l2m1，s为变量参数，(xpp,ypp,zpp)为式(9)表示的直线上任意一点的坐标，飞行器速度矢量的端点位于该交线上。

按下面的方式确定点(x0V,y0V,z0V)：

现在求出由捷联惯导系统得出的飞行器速度矢量的分量(xV,yV,zV)：

(10)

确定由式(9)表示的直线上与被式(10)确定的点最接近的点为

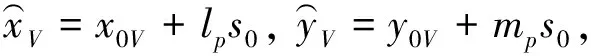
式中

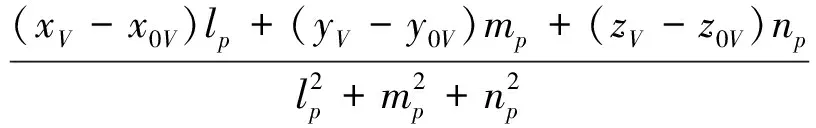
按下面的公式转换成速度矢量的投影

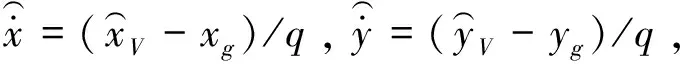
(11)

从而得出用捷联惯导系统确定飞行器速度时的误差

(12)

3 结论

介绍推导了一种根据相对2颗导航星的伪距离和伪速度的测量结果估计捷联惯导系统误差的解析方法，在可观测的卫星数量少于4颗时，该方法能保证以很高的精度计算捷联惯导系统的误差。

[1] 陈哲.捷联惯导系统原理[M].北京：宇航出版社，1986.

[2] Mohinder S Grewal, Lawrence R Weill, Augus P Andrews. 陈军, 易翔, 梁高波,等,译.GPS惯性导航组合[M]. 电子工业出版社,2011.

[3] 张勤,李家权,等.GPS测量原理及应用[M].北京：科学出版社， 2005.

[4] George T Schmidt,Richart E.Phillips INS/GPS Integration Architectures[C]∥Advances in Navigation Sensors and Integration Technology-RTO Lecture Series on 27～28 May 2004 in St.Petersburg ,Russia and on 31 May _1 June 2004 in Moscow,Russia.

[5] МББогданов,АВПрохорцов, ВВСавельев, ВАСмирнов. Способ оценки погрешностей бесплатформенной инерциальной навигационной системы в определении координат и скоростей по информации от двух навигационных спутников[J]. Изввузов Приборо- строение 2009, No 9.

[6] 高红铸,王敬庚,傅若男.空间解析几何[M].北京：北京师范大学出版社，2013，1.

TheMethodtoEstimatetheStrapdownIntertialNavigationSystemErrorAccordingtoTwoNavigationSatellitesInformation

YANG Xuelin1ZHANG Ying2
1. Beijing Institute of Aerospace Control Device, Beijing 100039, China 2. Beijing Aerospace Automatic Control Institute, Beijing 100854, China

Focusedonthehighlymotordrivenandshorttimeflyingaircraft,amethodwhichestimatesthepositionandvelocityerrorofthestrapdowninertialnavigationsystemisproposedinthispaperaccordingtoitsfakedistanceandfakevelocitybetweenthetwonavigationsatellites.Inviewoftherestrictionwhichiscausedbytheunlinearequationofdistanceandvelocitybetweenthefixedaircraftandeachsatellite,thevalueoftheerrorisgivenaccordingtotheminimumlengthconditionoftheseerrorvectors.Withtheanalyticgeometry,theerrorestimatedfinalmethodforstrapdowninertialnavigationsystemisdevived.Theunlinearminimumproblematicexactnessresultcanbeobtainedbyusingthismethod.

Navigationsatellite;Strapdowninertialnavigationsystem;Errorestimation;Analyticgeometry

2014-07-31

杨雪霖(1985-),女，北京人，硕士，工程师，主要研究方向为惯性设备和导航制导；张英(1982-),女，黑龙江人，硕士，工程师，主要研究方向为控制系统综合。

TP316.2

： A

1006-3242(2014)05-0021-03