随机介质理论在射水纠偏工程中的应用

潘 秀 徐 萍 魏 勇

(四川工程职业技术学院，四川 德阳 618000)

随机介质理论在射水纠偏工程中的应用

潘 秀 徐 萍 魏 勇

(四川工程职业技术学院，四川 德阳 618000)

利用随机介质理论研究了土散体颗粒移动的最基本问题，发现在射水掏土纠偏作用下土散体颗粒的移动概率可用正态分布函数表示，并由此得出射水掏土作用下同一层土体的沉降及射水孔对上部土体的作用范围，最后用工程实例验证了随机介质理论公式的实用性。

随机介质，射水掏土，移动概率方程

1 概述

射水掏土纠偏法在工程纠偏中广泛应用[1]。射水掏土是这样的过程：在建筑物沉降较小的一侧，设置一条射水坑或设置若干射水沉井，在建筑物基础下的一定深度处的坑内或井壁上布置一定数量的射水孔，通过射水孔用高压水枪伸入基础下进行长时间的连续冲水，使得沉降较小侧地基下的土以泥浆的形式从孔洞排出。该方法适用于土体为粘土或土质较硬、不方便掏土纠偏的倾斜房屋[2]。地基土体经高压水枪的冲蚀成孔后，孔壁的土体继续受到水流的冲刷，孔壁表面的土体源源不断的以泥浆的形式从孔洞排出，孔壁周围未被冲刷的土体在自重作用下补充被冲刷掉的土体[3]，故假定射水纠偏过程中射水冲出的孔洞维持在一个半径稳定的圆孔状态。土体是一种粘性散粒介质[4]，将地基土体视为体积相同的土颗粒散体的集合，射水掏土导致地基沉降过程可视为一个由底部散粒土体放出导致孔洞上部散体场移动的过程。射水掏土过程是一个复杂的宏观物理过程，土颗粒散体既表现出变化的力学响应，同时又伴随着土颗粒散体本身结构的变化[5]，这给数学建模及计算带来了极大的困难。由于土颗粒散体移动带有极强的随机性质，且土体是连续的，因而将土体简化为连续流动的随机介质，从概率论的观点去描述这类介质既可以避开散体复杂的本构研究，又能在宏观统计意义上建立相互制约的大量

颗粒群整体运动的规律。1957年，波兰科学院院士J.Litwiniszyn首先提出了随机介质理论的概念，并推导出岩土体在地下开采引起的移动规律的基本方程，即二阶抛物线型偏微分方程[6]。由于其方程在形式上与随机过程的方程相同，由此定义介质的移动方程可以用随机过程来描述的介质，即为随机介质。散体石英砂、碎石堆、开挖影响下的岩土体等均可看作随机介质。利用随机介质理论计算射水掏土作用下基础沉降的大致思路为：从概率统计理论出发，把整个射水掏土分解成无限多个微元掏土的总和。应用随机介质理论推导的概率式来推测该次微元掏土后土体场内土体颗粒的移动。将各次微元掏土产生的移动效果叠加，即可求得宏观上基础的沉降曲线及沉降量。

2 射水作用下土体散粒移动概率方程

2.1 基本假定

1)在射水纠偏过程中，地基下土体在射水作用下形成长柱形空洞，射水空洞的横截面面积相对于空洞的长度很小，因此可将射水形成的长柱形空洞上部土体的受力视为平面应变问题[7]，射水掏土引起的空洞上部土体位移视为平面位移问题。

2)实际土体颗粒之间具有较大的粘聚力和摩擦力，同时土体受到上部结构传递的荷载，因此射水掏土难以引起空洞上部土体的松散。故将受掏土作用影响的空洞上部土颗粒散体视为无膨胀散体(即散体颗粒在移动中无二次松散现象)[8]，其密度场在射水掏土作用中为均匀场。

2.2 土颗粒散体移动概率密度方程

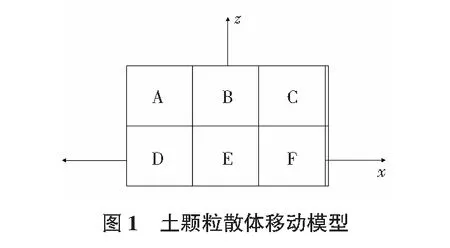
图1为土体颗粒三体的移动模型，假定坐标原点为理想放出口，任一土散体颗粒经理想放出口移出网格后，其原所在位置形成空位，空位由其上相邻方格里的颗粒随机递补。

由该移动模型可得土颗粒散体的平面移动概率密度方程：

(1)

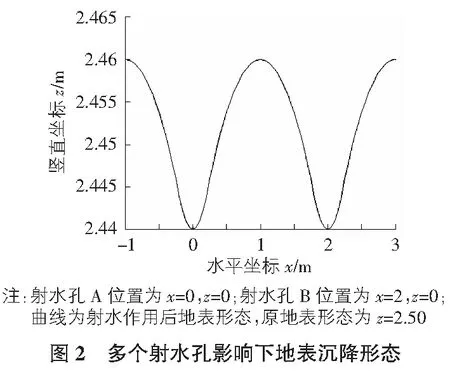
其中，x，z均为坐标值；k为散体的侧向填补系数，0

由2.1的平面假定可知：任意散体颗粒在其空间坐标(x，y，z)上的下移概率与y的取值无关，只是x和z的函数。平面应变假定中y的实际范围为长柱形空洞在y方向上的长度，假设形成的长柱形空洞长H0，则0≤y≤H0。

由式(1)可直接得出土颗粒散体空间移动的概率密度方程：

(2)

上述各参数的意义同前。

2.3 土颗粒散体移动范围的近似确定

工程中常用σ，2σ，3σ等来表征样本的取值范围[9]。根据散体下移概率分布，散体发生移动的概率随x(z轴对称时)的增大而增大，当z值确定时(同一层土体)，p(x，y，z)为关于x的标准正态分布。由正态分布概率积分表可知，在正态曲线下，±2.58σ所对应的概率积分面积为0.990 0。也就是说，在当|x|>2.58σ范围之外时，散体移动概率的可增加量仅为0.01，可见在散体移动场内，以2.58σ来确定散体移动范围足以满足精度的要求，即散体移动边界可近似为x=±2.58σ，可得移动边界的近似表达式为：

x2=6.66kz2-n0

(3)

可见近似移动边界是一条特定的颗粒移动迹线，将射水孔任一横截面上土颗粒散体每层土体的移动边界连接起来，可得一条介于直线和二次抛物线之间的曲线。

3 实例及结论

取江苏省淮安市某射水纠偏工程检验以上公式的实用性。欲使用上述公式推导该工程由射水作用引起的地表沉降量及射水作用对地表的影响范围，首先需要通过实验确定地基土的n0和k值。由随机介质放出实验可知该工程地基土的散体粘结性常数n0=0.61，散体侧向填补系数k=0.13。将实验n0和k值代入前文各公式中，最终可绘制出多个射水孔影响下该工程地表沉降形态，见图2，由图2可知地表上各点的沉降量最小为40 mm，最大为60 mm。这与实测的房屋受射水纠偏作用引起的沉降量相近，可见运用随机介质理论预测射水掏土纠偏中土体的移动规律是具有很强的实用性的。

由上述分析可知，射水掏土作用可用随机过程阐释，由随机介质理论可知土颗粒散体空间移动的概率密度方程为式(1)。在射水截面上，同一层土体沉降随着放出来Qf增大呈变化的漏斗状，如图2所示。由式(3)能近似确定射水孔作用的影响范围。最后用工程实例验证了随机介质理论公式的实用性。这些推导结果对实际射水纠偏工程射水量的控制、射水后地表沉降效果及射水孔埋设位置的确定有一定的预测指导作用。

[1] 陈希哲.地基事故与预防[M].北京:清华大学出版社，1996.

[2] 李惠强.建筑结构诊断鉴定与加固修复[M].武汉:华中科技大学出版社，2012.

[3] 胡 军.冲淤纠偏加固施工技术[J].建筑技术,2002,33(6):417-419.

[4] 吴爱祥.散体动力学理论及应用[M].北京：冶金工业出版社，2010.

[5] 王铁行，廖红建.岩土工程数值分析[M].北京：机械工业出版社,2009.

[6] HE Yue-guang,LIU Bao-chen.Stochastic Medium Theory in Analyzing the Displacement and Deformation Resulting from Excavating Slope Ground Mass[J].Journal of Changsha Communications University,2006,22(3):1-5.

[7] 徐芝纶.弹性力学[M].北京:高等教育出版社,1990.

[8] 黄松元.散体力学[M].北京：机械工业出版社，1993.

[9] 王颖喆.概率与数理统计[M].北京：北京师范大学出版社，2005.

[10] 同济大学.高等数学[M].北京：高等教育出版社，2007.

[11] 谢树艺.工程数学——矢量分析与场论[M].北京：高等教育出版社，2005.

[12] 任凤玉.随机介质放矿理论及其应用[M].北京：冶金工业出版社，1994.

[13] 汪荣鑫.数理统计[M].西安：西安交通大学出版社，2007.

Law of soil movement with influence of water jetting

PAN Xiu XU Ping WEI Yong

(SichuanEngineeringTechnicalCollege,Deyang618000,China)

Combinating the random medium theory with water jetting technology, we can research the most basic question of soil movement. The movable probability equation of soil dispersion can be described as a normal distribution function. Therefore we can know influence range of water jetting for soil in the above of jet hole, proves by the engineering example that the random medium theory is practical.

random medium， water jet cutting soil， probability equation

1009-6825(2014)11-0094-02

2014-01-21

潘 秀(1987- )，女，硕士，助教； 徐 萍(1986- )，女，硕士，助教； 魏 勇(1986- )，男，硕士，助教

TU411.2

A