伊利石软岩铁路隧道开挖的有限元分析

李 鹏

(太原市市政公用工程质量监督站，山西 太原 030006)

伊利石软岩铁路隧道开挖的有限元分析

李 鹏

(太原市市政公用工程质量监督站，山西 太原 030006)

针对伊利石软岩中单线铁路隧道的开挖特点，采用弹塑性、非线性和大变形的力学模型及岩土工程中常用的Drucker-Prager准则，运用ANSYS软件进行数值分析，并从伊利石软岩的位移、应力角度出发，得出伊利石软岩的力学特性、滑动特性以及要加强对边墙部位支护的结论。

伊利石软岩，铁路隧道，数值分析，力学特性

0 引言

岩体在隧道开挖过程中会受到不同程度的扰动，在岩性不好的地层中，如研究岩体在开挖过程中软岩的稳定性，对于隧道的开挖有着重要的意义[1,2]。对于伊利石软岩的研究方法有很多，工程中围岩的稳定性问题一直是岩土工程一个重要的研究内容，而软岩的滑动特性在隧道工程方面表现的尤为突出[4,5]。本文所研究的伊利石属于软岩结构，其强度、稳定性都非常差。如果隧道开挖时，伊利石作为隧道围岩结构，很容易引起涌水、塌方、岩溶塌陷，以及因高地应力引起的围岩挤压而产生大变形等一系列问题。因此有必要对伊利石软岩的滑动特性进行研究，并且在研究的过程中，应给软岩需采取的防护措施以有效的建议[6,7]。本文将隧道工程与软岩的滑动特性研究相结合，即以隧道工程作为研究背景，对隧道开挖后，由伊利石软岩构成的围岩进行ANSYS数值模拟，得出隧道围岩的滑动特性等力学性质，进而得出伊利石软岩的滑动特性，是研究伊利石软岩的最好方法。

1 ANSYS计算模型及计算参数

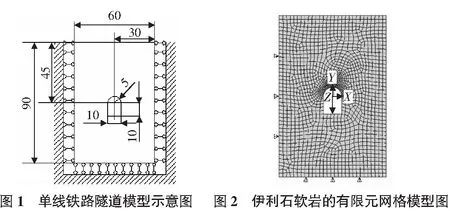
1)伊利石软岩模型尺寸。隧道埋深为40 m(属于浅埋式隧道)，隧道全长500 m(由于隧道开挖是分阶段开挖，且伊利石软岩的稳定性差，不宜大段开挖，所以先取开挖长度为10 m)，围岩为伊利石软岩，属于第Ⅳ类岩石，拱顶半径R=5 m,洞高H=15 m，宽度B=10 m，水平方向左右各取25 m，隧道底部以下取35 m，隧道模型示意图如图1所示。

2)伊利石软岩模型类型。根据实际中隧道的设计规格，建立的伊利石软岩模型范围根据弹塑性理论影响范围选取，一般取3倍～5倍的洞径。由前面理论得知，为使得出的结果更精确，可以取10倍以上的范围。此隧道为单线铁路隧道，该隧道位于陡峭山体，隧道平面设计为直线，横断面设计为直墙式单线铁路隧道，且不带仰拱。本文只考虑自重产生的初始应力场，重力加速度取9.8 m/s2。

3)伊利石软岩的计算边界。为尽量减少模型中边界约束条件对计算结果产生不利的影响，计算模型的边界范围按照以下原则进行确定：

a.计算模型所取地层的范围是：水平方向左、右边取洞跨的6倍；垂直方向，上边界为自由地表，下边界为洞高的3.5倍；计算时所施加的边界约束条件是：地表为自由边界，未加任何约束；计算模型的左右边界分别受到X轴方向的位移约束，模型的地层下部边界受到Y轴方向的位移约束，有限元划分网格模型如图2所示。b.在分析计算中采取目前有限元分析中比较常用的弹塑性模型，屈服准则采用岩土工程中常用的Drucker-Prager准则，其本构采用非线性、各向同性模型，并考虑岩体的弹塑性及大变形。

4)伊利石软岩的力学参数。计算中采用理想弹塑性材料，屈服准则采用Drucker-Prager准则。围岩材料的力学参数采用隧道围岩的实测值。根据铁路隧道设计规范，伊利石软岩的力学参数见表1。

表1 伊利石软岩的力学参数

2 ANSYS计算结果分析

1)隧道围岩位移特征。单线铁路隧道开挖后围岩位移变形模态如图3所示。由于单线铁路隧道开挖后引起应力重分布，从图3中可以看出围岩和隧道整体向下变形，且围岩的变形仅限于一定范围内，且拱顶、边墙和底板处发生较大位移。

从伊利石软岩的各方向最大位移矢量表2得出：开挖后伊利石软岩在X方向上围岩的最大位移量为2.1×10-3m，Y方向上围岩的最大位移量为5.9×10-2m。对于围岩为伊利石软岩的隧道，在深度为40 m处，采用浅埋直接暗挖法施工，对X方向位移影响不大，对Y方向位移影响大。由位移矢量云图知：边墙和拱顶的位移影响较大，已出现大变形破坏，岩层被拉裂分开，因此在隧道开挖时需要对伊利石软岩加锚杆以及钢筋混凝土支护，防止隧道发生坍塌等事故。

表2 伊利石软岩的各方向最大位移矢量列表 m

由图4得出：隧道开挖后所产生的变形量沿高度(Y方向)的变化越来越小，距离3倍洞径以外岩体下部位移量很小，基本上不受隧道开挖影响，围岩开挖深度受开挖后卸载的影响很小；在隧道顶部，围岩的位移量达到最大。在3倍距离内，拱顶和边墙都受到很大的力的作用，产生明显的位移，一般要在其拱顶处加锚杆支护。所以隧道开挖后，未加支护前，围岩的位移较大，伊利石软岩稳定性差，容易变形。

2)隧道围岩应力特征。从图5～图8可以看出，隧道开挖后，在洞径1倍的区域内受开挖影响较大，3倍区域以外受开挖影响较小，且距离隧洞越远，影响越小。隧道开挖前由自重应力形成的初始应力场呈层状分布。由于开挖后的卸载作用，产生应力重分布，分别形成应力松弛区和应力集中区。由图5和表3得出：X方向的围岩应力主要集中在隧道拱脚与边墙连接的位置，其最大值为6.2×105Pa，应力最小处为隧道的底部，其值为3.8×105Pa；由图6和表3得出：Y方向的应力主要集中在隧道底部与边墙连接的位置，其值为2.0×106Pa，应力最小处为拱顶和隧道底部位置，其值为5.5×103Pa；由图8和表3得出：XY方向的剪切应力主要集中在拱顶两侧和隧道底部与边墙连接处，并且呈对角线分布，最大值为6.6×105Pa，并且在各自对角线上应力方向相同，主对角线受拉，副对角线受压；由图7和表4得出：隧道围岩的等效应力主要集中在隧道底部与边墙连接的位置和隧道拱顶与边墙连接的位置，最小值分布在隧道底部和隧道顶部。

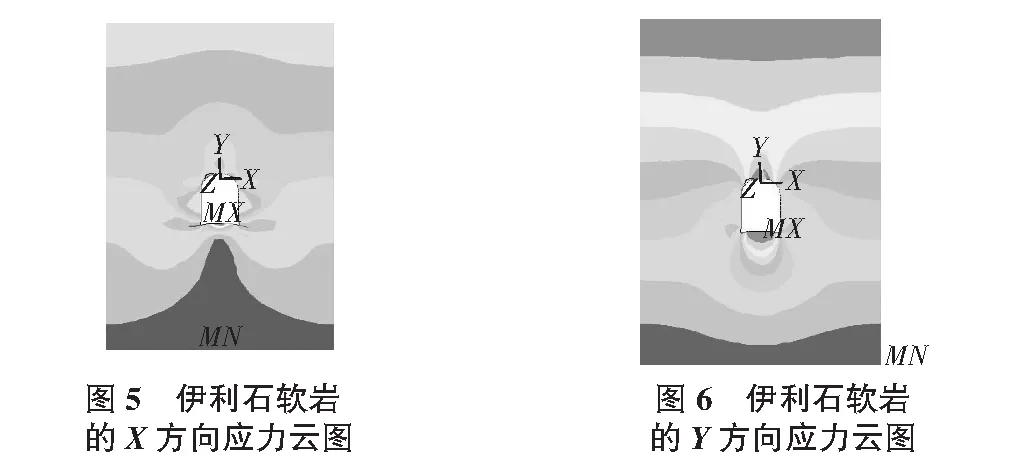
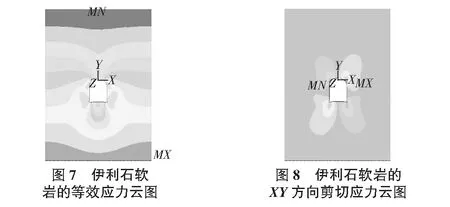
表3 伊利石软岩的各方向应力最值表

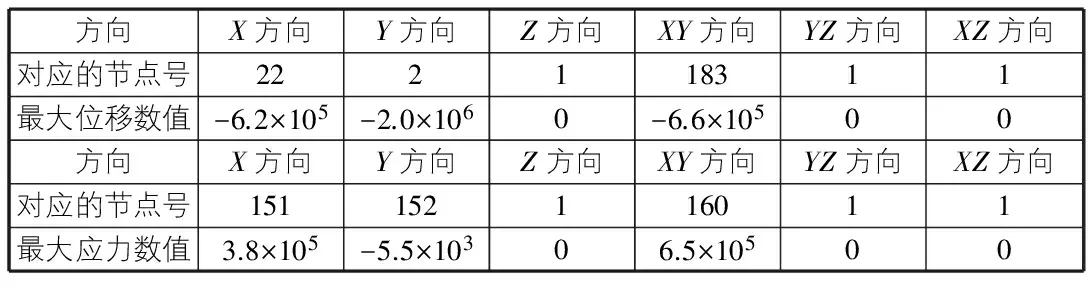
Pa

应力松弛区主要分布在拱顶位置，处于受压状态，且伊利石围岩强度不够高，产生很大的压应力；在隧道底部位置，处于受拉状态，且伊利石围岩强度不够高，产生很大的拉应力。由于单线铁路隧道的边墙设计比较高，洞底的应力松弛区范围明显。由于边墙较高，由图7可以看出，在边墙与底部连接部位出现较大的应力区，所以要加强对边墙部位的支护，通常用横隔板和边墙支架来加强边墙的受力。由图5～图8得出，隧道开挖前由自重应力形成的初始应力场呈层状分布。隧道开挖后，应力从地面到地面以下依然呈层状分布。由于开挖后应力重分布效应，应力大小沿高度依次递减，导致最底部的应力最大，地面表层应力最小，可以忽略不计。

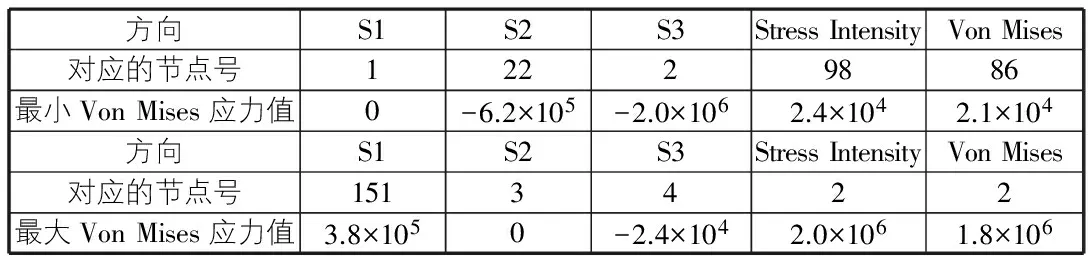
表4 伊利石软岩的Von Mises应力最值表 Pa

3 结语

本文将隧道工程与软岩的滑动特性研究相结合，即以隧道工程作为研究背景，对隧道开挖后，由伊利石软岩构成的围岩进行ANSYS数值模拟，得出隧道围岩的滑动特性等力学性质，进而得出伊利石软岩的滑动特性，得到应力主要集中在隧道底部与边墙连接的位置和隧道拱顶与边墙连接的位置，所以要加强对边墙部位的支护；最小值分布在隧道底部和隧道顶部。

[1] 侯召松,刘志汉,李云龙，等.岩体隧道开挖过程中围岩稳定性的数值分析[J].科技创新导报,2010(20):54.

[2] 秦玉红.地下洞室围岩稳定分析法的研究现状[J].现代矿业,2009(5):24-27.

[3] 张 彬,刘 波.ANSYS在软岩巷道围岩稳定性分析中的应用[J].山西建筑,2009,35(30):82-83.

[4] 刘 永,谭显坤,张 航.椿树垭隧道岩体结构特征与围岩稳定性分析[J].安全与环境工程,2010,17(5):106-112.

[5] 孙 钧.岩土材料流变及其工程应用[M].北京:中国建筑工业出版社,1999.

[6] J Owen DRJ,Hinton E.Finite Elements in Plasticity:Theory and Practice[M].Swansea,Pine Ridge Pres8 Limited,1980.

[7] 徐 军,郑颖人.隧道围岩弹塑性随机有限元分析及可靠度计算[J].岩土力学,2003,24(1):70-74.

Finite element analysis of Illite soft rock railway tunnel excavation

LI Peng

(TaiyuanMuniciplePublicEngineeringQualitySupervisionStation,Taiyuan030006,China)

According to the excavation features of Illite soft rock single-line railway tunnel, the paper adopts the elastic-plastic, non-linear and large deformation dynamic models and the common Drucker-Prager principle of geotechnical project, undertakes the numeric analysis by adopting ANSYS software, concludes the dynamic features and the sliding features of Illite soft rock from its displacement and stress, and the side wall support should be enhanced.

Illite soft rock, railway tunnel, numeric analysis, dynamic feature

2014-06-30

李 鹏(1978- )，男，工程师

1009-6825(2014)27-0169-02

U455

A