表面波纹度对滚动轴承-转子系统非线性振动的影响
顾晓辉, 杨绍普, 刘永强, 廖英英
(石家庄铁道大学 机械工程学院, 石家庄 050043)
表面波纹度对滚动轴承-转子系统非线性振动的影响
顾晓辉, 杨绍普, 刘永强, 廖英英
(石家庄铁道大学 机械工程学院, 石家庄 050043)
分析了考虑滚动轴承内外圈波纹度、径向间隙和非线性赫兹力作用下的滚动轴承-转子系统非线性动力学响应。根据不同参数下的分岔图、功率谱图和庞加莱截面图,研究了轴承表面波纹度最大幅值和转速对系统的非线性振动的影响,找到了不同故障类型的特征频率。根据分形理论应用G-P算法计算了相同转速下不同最大幅值时的关联维数。分析结果表明,当系统处于混沌状态时随着波纹度最大幅值的增加,其关联维数也会相应增大。因此关联维数可以应用于轴承故障的特征提取与定量诊断中。
滚动轴承;非线性动力学;波纹度;关联维数;混沌
作为旋转机械的核心部件,轴承-转子系统的研究一直深受科研工作者的关注[1-4]。滚动轴承的内、外圈滚道和滚动体表面波纹度是在生产过程中产生的一种加工误差,已有研究表明波纹度是滚动轴承-转子系统产生振动和噪声的主要原因之一,另外在滚动轴承的使用过程中由于疲劳或润滑不良等因素也会加大波纹度的最大幅值,对系统产生不利的影响。因此,对于高速、重载化的转子系统来说,波纹度的影响不容小觑。文献[5]建立了滚动轴承在外圈滚道波纹度激励下的非线性接触噪声模型,研究了波纹度参数与噪声的关系。文献[6-7]建立了考虑滚动轴承表面波纹度的轴承-转子系统动力学模型,分别研究了系统中含有不同滚动体个数和表面波纹个数时系统的非线性动力学响应,发现当滚动体个数等于波纹个数时,系统会产生强烈的振动。本文在前人研究的基础上分析了内、外圈滚道波纹度最大幅值对系统的非线性振动的影响,并用分形理论计算了不同波纹度幅值时的关联维数,为系统的故障识别与定量诊断提供了理论依据。
1 系统模型
1.1 转子-轴承系统模型
本文的研究对象是两端用滚动轴承支承的单盘转子系统,圆盘的等效质量为2m,偏心距为e,并受一个恒定的径向力2W,如图1所示。
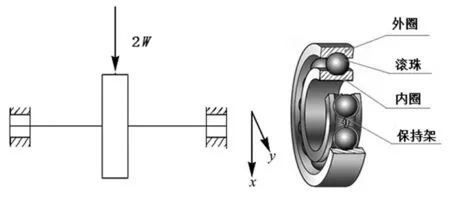
图1 滚动轴承及滚动轴承-转子系统示意图Fig.1 Schematic diagram of a rolling bearing-rotor system and a rolling bearing
1.2 表面波纹度模型
本文忽略滚珠的波纹度影响,只考虑内、外圈滚道上的波纹度。假设外圈波纹度最大幅值为A0,初始相位角为φ0,则有:
(1)

假设滚动轴承外圈固定,内圈固结于转轴,外圈转速ωo=0,线速度vo=0,内圈转速ωi=ω,线速度vi=ωRi。ω为转轴角速度,Ri为内圈滚道半径。则保持架的线速度
(2)
角速度为
(3)
则在t时刻接触点角位置为
(4)
其中,Nb为滚动体个数。
因此外圈波纹度可表示为
(5)
同理,可得内圈波纹度表达式为:
(6)
1.3 滚动轴承的非线性赫兹力
在转子运转过程中,轴承中的滚珠与内、外圈滚道相接触,假定其弹性接触满足赫兹理论,忽略润滑油的影响,则第i个滚珠处的恢复力可表示为
(7)

γθi=xcosθi+ysinθi-(γ0+A)
(8)
其中,x和y为图1所示坐标系x和y方向内圈几何中心偏移量,γ0为滚动轴承径向间隙。
因此,第i个滚珠处的恢复力为
(9)
则滚动轴承总恢复力在x和y方向的分力可以表示为
(10)
(11)
1.4 系统动力学方程
假设系统为对称支承的水平刚性转子,由牛顿定律可得系统的非线性振动方程:
(12)
(13)
式中,c为轴承阻尼,由文献[3]得c=33.75~337.5 N·s/m,本文取c=300 N·s/m。由于本文主要研究滚动轴承表面波纹度,所以忽略转子系统的偏心影响,认为e=0。
2 系统的非线性动力学响应分析
本文研究的滚动轴承-转子系统包含滚动轴承径向间隙、非线性恢复力等强非线性因素,采用龙格—库塔法求解,并用小步长计算1 100个周期,并去掉前1 000个周期,取后100个周期的稳定的结果。采用相同的系统参数,分别研究了不同最大幅值和转速下系统的非线性运动特性。
滚动轴承参数如下表:

表1 滚动轴承参数
2.1 不考虑波纹度时系统的响应
图2为不考虑波纹度的影响时内圈几何中心偏移位移x方向的分岔图,可以看出系统在小于3 600 r/min区间内运动较为复杂,以周期运动和混沌运动为主,因此系统在启动时应快速通过,尽量减少在此阶段的时间。图3(a)为n=3 230 r/min时的x方向功率谱图和庞加莱截面图,此时系统处于混沌状态,功率谱图中的峰值对应着VC频率(即变柔度振动频率)的基频和倍频。系统在4 000 ~10 000 r/min和15 000 ~100 000 r/min区间工作时处于稳定的周期运动,系统的工作转速应该选在这两个区间中。图2(b)为图2(a)的局部放大图,从图2(b)中可以看出系统在10 000~15 000 r/min区间工作时处于拟周期运动和周期运动相互交替的过程。图3(b)为n=11 800 r/min时的x方向功率谱图和庞加莱截面图,从功率谱图和庞加莱截面图中可以明显地看出系统作周期六运动。图3(c)为n=14 600 r/min时的x方向功率谱图和庞加莱截面图,功率谱图中有两个不可相约的频率分量和庞加莱截面图中的封闭圆环说明系统作拟周期运动。

图2 不考虑波纹度时x方向分岔图Fig.2 x displacement bifurcation diagram without waviness

图3 x方向功率谱图和庞加莱截面图Fig.3 The power spectra and Poincaré map
2.2 仅考虑外圈波纹度时系统的响应

图4 Ao=0.5 μm时x方向分岔图Fig.4 x displacement bifurcation diagram at Ao=0.5 μm
图4为外圈波纹度最大幅值为0.5μm时x方向的分岔图,在小于5 000 r/min时其运动与无波纹度时基本保持一致,并且在6 400 ~12 700 r/min区间作稳定的周期一运动,在17 000~23 500 r/min区间作稳定的周期二运动。不同的是在12 700 ~15 000 r/min区间内系统先是作混沌运动然后作周期九运动最后作拟周期运动。图5为n=10 000 r/min、13 180 r/min和14 600 r/min时的x方向功率谱图和庞加莱截面图,可以看出其主要频率成分为fbpo(即滚动体通过外圈频率)。

图5 x方向功率谱图和庞加莱截面图Fig.5 The power spectra and Poincaré map
当最大幅值扩展到1 μm时,系统作稳定周期运动的区间明显减少。从图7中的功率谱图中亦可以找到特征频率fbpo或1/2fbpo,因此此频率成分可以作为外圈滚道波纹度故障识别的依据。
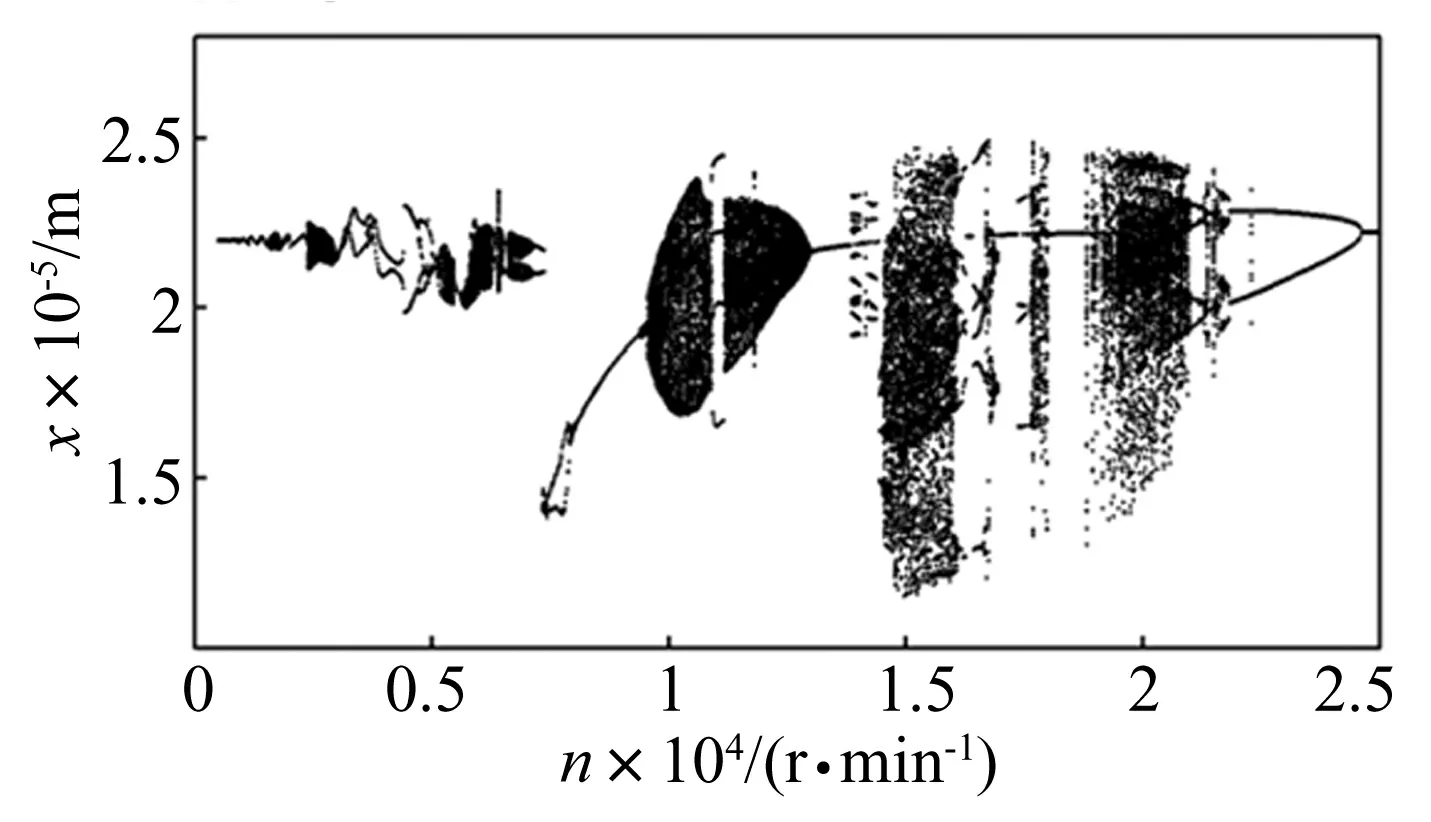
图6 A0=1 μm时x方向分岔图Fig.6 x displacement bifurcation diagram at A0=1μm

图7 x方向功率谱图和庞加莱截面图Fig.7 The power spectra and Poincaré map
2.3 仅考虑内圈波纹度时系统的响应
在只考虑内圈滚道波纹度时,与前文不同的是系统的运动以拟周期运动和混沌运动为主,并出现相互交替的现象,没有较大的周期运动区间。图8为Ai=0.5 μm时n=1 000 r/min、7 500 r/min和20 000 r/min时x方向的功率谱图和庞加莱截面图,从功率谱图中可以看出,其主要的频率成分为fbpo和fbpi-f(即滚动体通过内圈频率与内圈旋转频率的差)。图9为内圈波纹度扩展到1 μm时三种相同转速下的功率谱图和庞加莱截面图,可以看出系统的运动形式基本没有改变,并且有相同的故障特征频率。
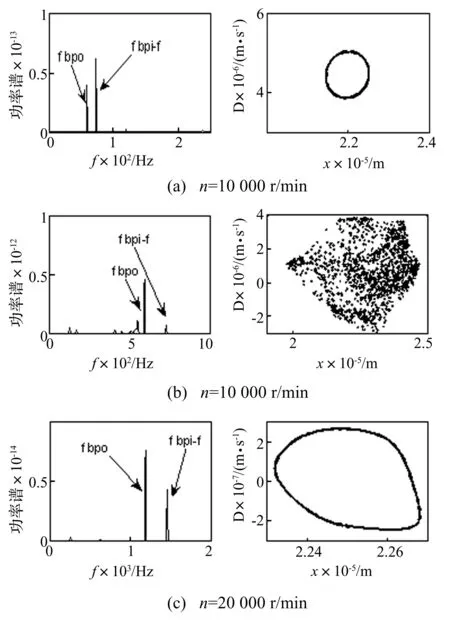
图8 x方向功率谱图和庞加莱截面图Fig.8 The power spectra and Poincaré map

图9 x方向功率谱图和庞加莱截面图Fig.9 The power spectra and Poincaré map
2.4 考虑内圈和外圈波纹度时系统的响应
内外圈滚道波纹度最大幅值皆为0.5 μm时,系统在低速和高速区间内表现为拟周期运动,在中间区域内表现为混沌运动和拟周期运动相互交替的形式。图10为n=1 000 r/min、7 500 r/min和20 000 r/min时的x方向功率谱图和庞加莱截面图,从中可以前文所述的两种故障特征频率fbpo和fbpi-f。
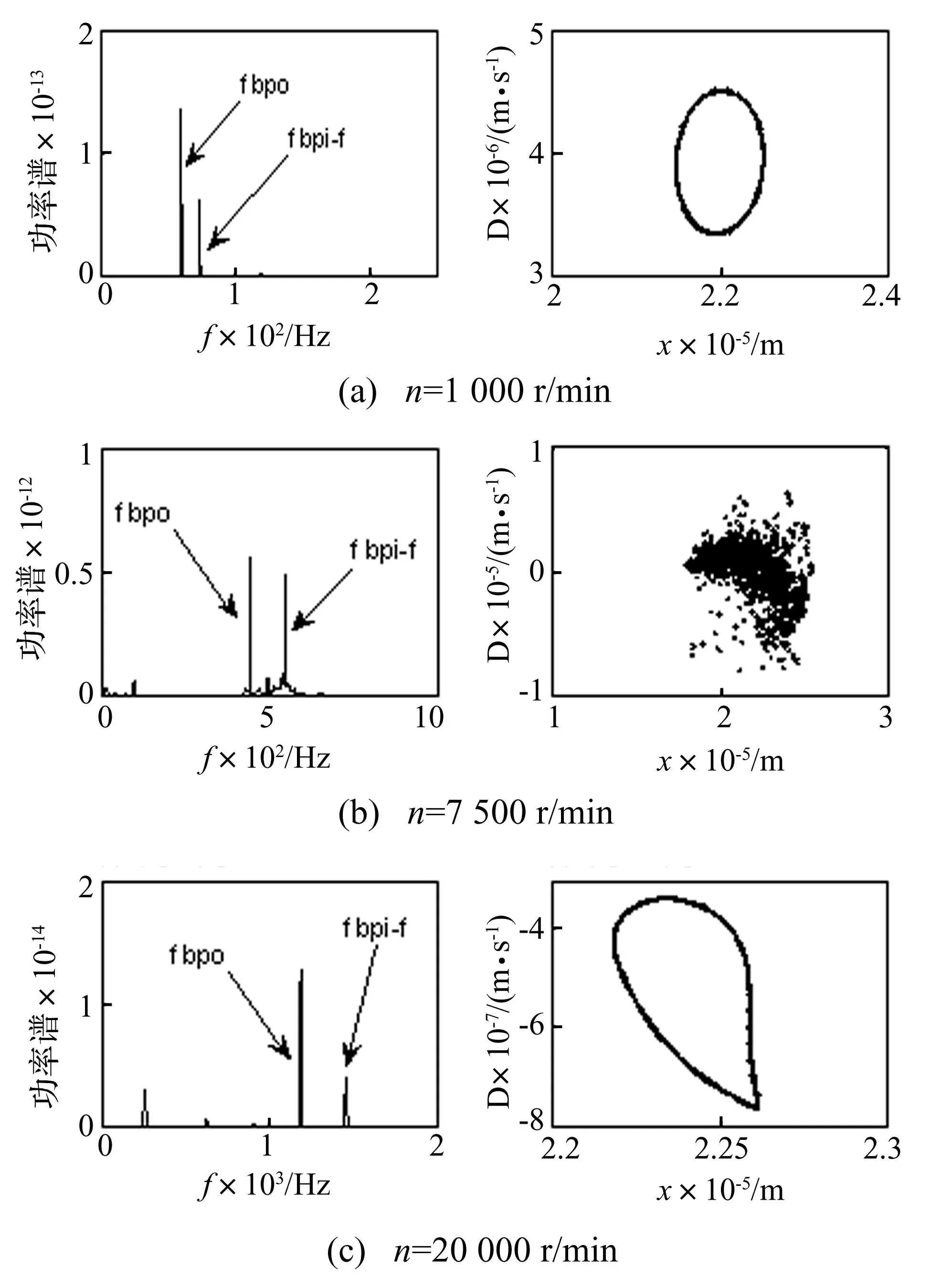
图10 x方向功率谱图和庞加莱截面图Fig.10 The power spectra and Poincaré map
3 用关联维数判别系统波纹度故障程度
在波纹度慢变扩展过程中可发现,系统在某一转速下,不同的波纹度类型可以依靠特征频率进行区分,但是波纹度故障程度通过普通的频谱分析方法很难诊断,其响应在时域和频域上并没有明显的特征信息,缺乏定量分析的依据。图11为当转速为15 000 r/min时A0为2.5 μm、3.5 μm、4 μm和4.5 μm时x方向位移响应的频谱图。

图11 n=15 000 r/min时x方向位移响应的频谱图Fig.11 The spectrogram in x displacement at n=15 000 r/min
为解决以上问题,本文应用分形理论,计算系统的非线性时间序列的关联维数,用于波纹度程度的定量识别。由于在生产实践中外圈出现故障的概率大于内圈和滚动体等部件,所以下文的研究只考虑了外圈滚道的波纹度。
对于时间序列x1,x2,…,xn-1,xn,选定嵌入维数m和时间延迟τ重构相空间X(i)
Xi=[x(i),x(i+τ),x(i+2τ),…,
x(i+(m-1)τ]
i=1,2,…
(14)
其中,M=N-(m-1)τ。按照Takens定理,重构的相空间可以在拓扑等价的意义下恢复吸引子的相空间。本文选用文献[9]中提出的G-P算法在重构的相空间基础上,计算关联积分
(15)
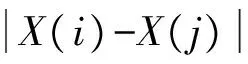
对于无噪声的、无限长的时间序列,时间延迟τ可以任意选取,但对本文中的有限长序列,时间延迟τ对重构的相空间至关重要。目前采用的方法一般有自相关法、复相关法、互信息量法和C-C方法等,本文选用方法简单、易于计算的自相关法求时间延迟τ。计算结果见表2。
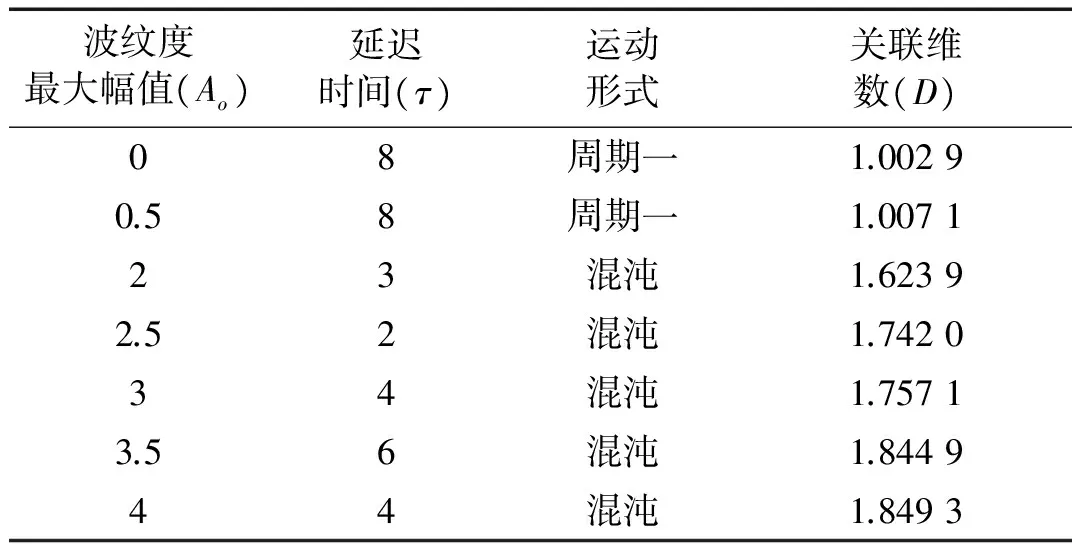
表2 不同最大幅值下的关联维数
当Ao为0 μm和0.5 μm时,在15 000 r/min时系统作周期一运动,计算的关联维数为1.002 9和1.007 1,非常接近于理论值1。当Ap逐渐增大时,相应的关联维数也逐步增大,这表明关联维数可以很好地应用于这种非线性故障的特征提取与定量诊断。
4 结 论
本文建立了考虑滚动轴承内外圈波纹度、径向间隙和非线性赫兹力作用下的滚动轴承-转子系统非线性动力学模型,分析了轴承表面波纹度最大幅值对系统的非线性振动的影响。结果表明不同的波纹度类型对应着不同的故障特征频率,而在相同的故障类型下,在系统处于混沌时,从频谱图上找不到明显的特征信息以识别表面波纹度的严重程度的情况时,本文采用G-P算法计算了系统在不同最大波纹度幅值时的关联维数,研究发现随着故障程度的增加,关联维数逐渐增大。
[ 1 ] 闻邦椿,武新华,丁千,等. 故障旋转机械非线性动力学的理论与试验[M]. 北京:科学出版社,2004.
[ 2 ] 黄文虎,夏松波,焦映厚,等. 旋转机械非线性动力学设计基础理论与方法[M]. 北京:科学出版社,2006.
[ 3 ] Tiwari M,Gupta K,Prakash O. Effect of radial internal clearance of a ball bearing on the dynamics of a balanced horizontal rotor[J]. Journal of Sound and Vibration, 2000, 238(5): 723-756.
[ 4 ] Tiwari M,Gupta K,Prakash O. Dynamic response of an unbalanced rotor supported on ball bearings[J]. Journal of Sound and Vibration, 2000, 238(5): 757-779.
[ 5 ] 殷玉枫,张闯. 表面波纹度激励下的滚动轴承非线性接触噪声分析[J]. 噪声与振动控制,2011, 31(1): 43-47. YIN Yu-feng,ZHANG Chuang. Analysis of noise due to surface-waviness induced nonlinear contact in rolling bearing[J]. Noise and Vibration Control, 2011, 31(1): 43-47.
[ 6 ] Harsha S P, Kankar P K. Stability analysis of a rotor bearing system due to surface waviness and number of balls[J]. International Journal of Mechanical Sciences, 2004, 46(7): 1057-1081.
[ 7 ] 张耀强, 陈建军, 邓四二, 等. 考虑表面波纹度的滚动轴承—转子系统非线性动力特性[J]. 航空动力学报, 2008, 23(9): 1731-1736. ZHANG Yao-qiang, CHEN Jian-jun, DENG Si-er, et al. Nonlinear dynamic characteristics of a rolling bearing-rotor system with surface waviness[J].Journal of Aerospace Power, 2008, 23(9): 1731-1736.
[ 8 ] Harris T A. Rolling bearing analysis[M]. New York: Willey, 2001.
[ 9 ] Grassberger P,Procaccia I. Measuring the strangeness of strange attractors[J]. Physica D:Nonlinear Phenomena, 1983, 9(1-2): 189-208.
[10] 杨绍普,申永军. 滞后非线性系统的分岔与奇异性[M]. 北京:科学出版社,2003.
Effect of surface waviness on nonlinear vibration of a rotor with ball bearings
GU Xiao-hui,YANG Shao-pu, LIU Yong-qiang,LIAO Ying-ying
(School of Mechanical Engineering, Shijiazhuang Railway University, Shijiazhuang 050043, China)
The nonlinear dynamic response of a rotor with ball bearings considering nonlinearities of surface waviness, internal radial clearance and Hertzian contact force was analyzed and the results were presented in the forms of bifurcation diagram, power spectrum and Poincaré map. The effects of maximum amplitude of waviness and rotating speed on the nonlinear vibration of the rotor system were studied and characteristic frequencies of different faults were found. G-P method was used to calculate the correlation dimension number for different maximum amplitudes under the same rotating speed. The results showed that the correlation dimension number increases with increase in the maximum amplitude of the waviness when the system is in a chaos; the correlation dimension number can be applied in extraction and quantitative diagnosis of faults.
rolling bearing; nonlinear dynamics; surface waviness; correlation dimension number; chaos
国家自然科学基金项目(11172182,11227201,11202141);铁道部重点项目 (2011J013-A);河北省教育厅项目 (Z2011228)
2013-01-17 修改稿收到日期:2013-05-29
顾晓辉 男,硕士生,1988年11月生
TH133.33;O322
A
10.13465/j.cnki.jvs.2014.08.019

