一个数学问题的探究

朱 华 东

(江苏省石庄高级中学，江苏如皋 226531)

一个数学问题的探究

朱 华 东

(江苏省石庄高级中学，江苏如皋 226531)

对《数学通报》2013年第7期刊登的第2126号问题圆的外切四边形的一个性质进行探究.考虑能否推广至圆的外切多边形，再进一步探究椭圆外切四边形的一个性质，体会对数学问题探究从特殊到一般的方法.

圆外切多边形；椭圆外切四边形；定值

《数学通报》2013年第7期刊登的第2126号问题是：

已知四边形ABCD是⊙I的外切四边形，则下列恒等式成立：

此结论可否推广至更一般的情形，本文进行了探究性研究，获得了一些有趣的结论.

1 可否推广

问题2126可否推广到有内切圆的多边形中呢.

若n边形A1A2…An是⊙I的外切n边形，是否有

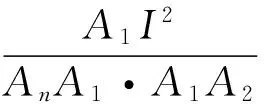
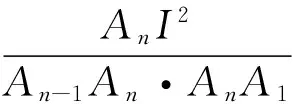
其中f(n)是仅与多边形边数n有关的函数.由问题2126，f(4)=2.

若以上猜测成立，f(n)的表达式应为什么呢？显然猜测成立时，当n边形A1A2…An是正n边形时也成立.据此，我们可求出f(n).

如图1，设正n边形A1A2…An的内切圆⊙I与AnA1相切于Hn，设IHn=1，则

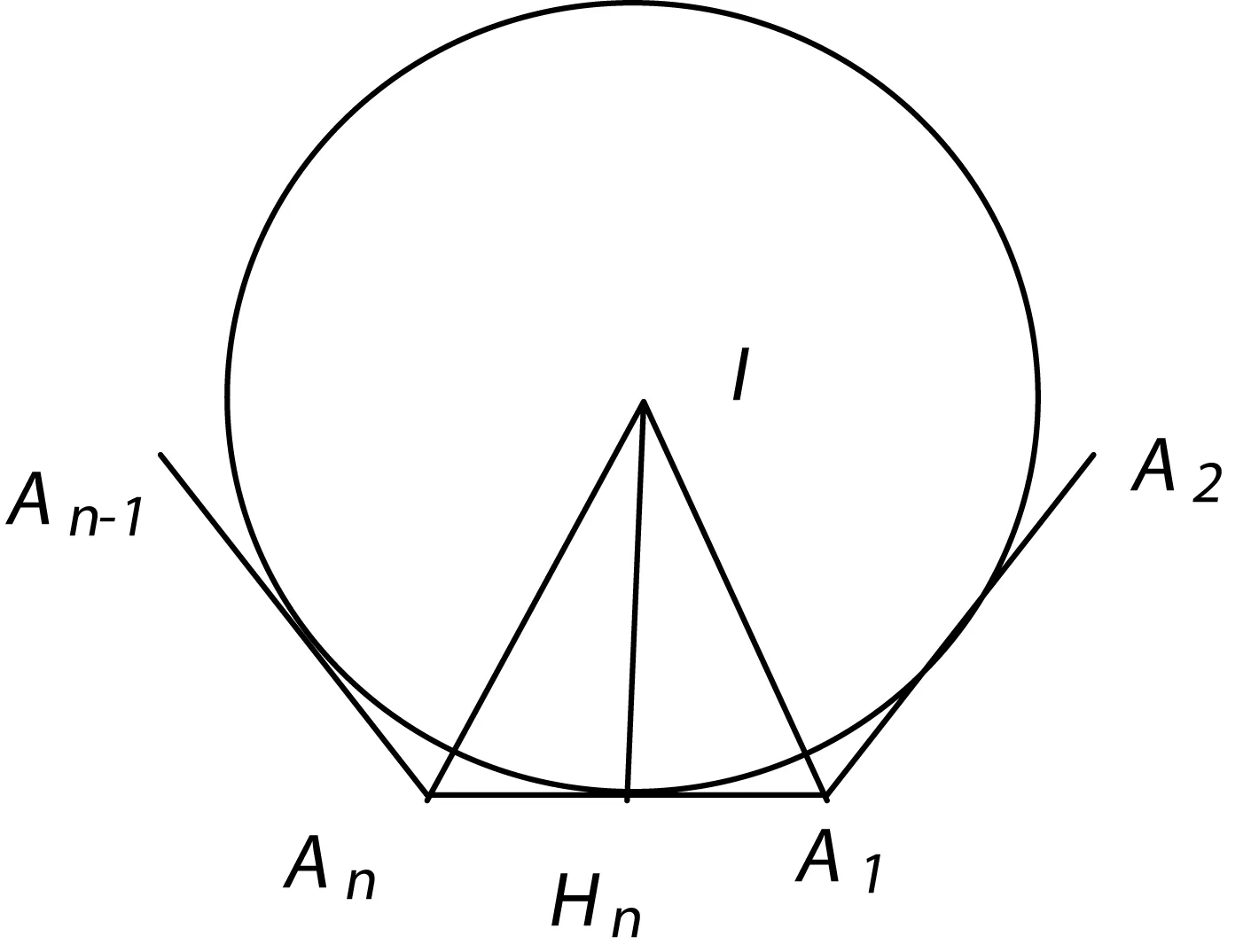
图1

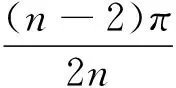
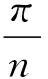
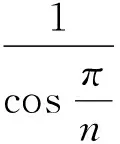
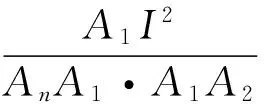
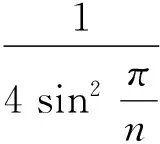
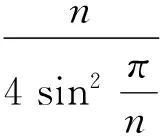
综上，提出猜想：若n边形A1A2…An是⊙I的外切n边形，则

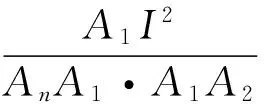
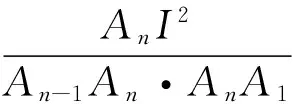
我们来否定这个猜想.

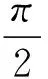
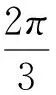
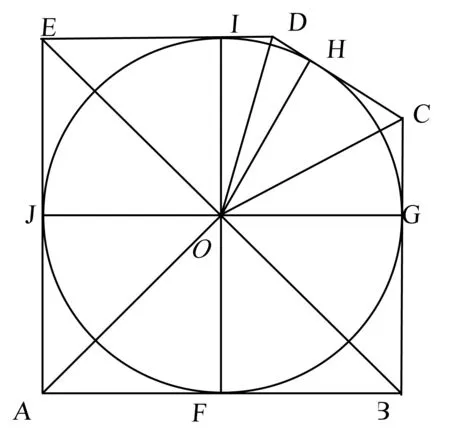
图2

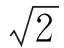
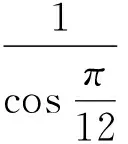
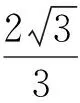
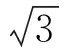
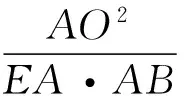
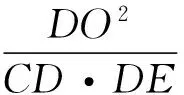
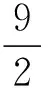
2 另辟蹊径

圆的圆心在椭圆中既可看作中心，也可看作两个焦点，即圆也可看作有两个焦点，只不过两个焦点重合于圆心而已.根据这一观点，我们可以提出如下一个问题：

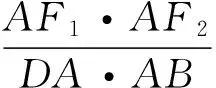
探究如下：

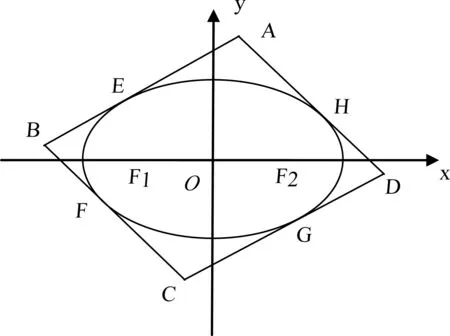
图3

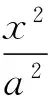
(a>b>0)的外切四边形，F1(-C,0),F2(C,0).切点分别为E,F,G,H,设E(acosθ1,bsinθ1),F(acosθ2,bsinθ2),G(acosθ3,bsinθ3),H(acosθ4,bsinθ4),则直线DA的方程为：

xbcosθ4+yasinθ4=ab,

(1)

直线AB的方程为：

xbcosθ1+yasinθ1=ab.

(2)

(1), (2)联立，解之得：

(3)

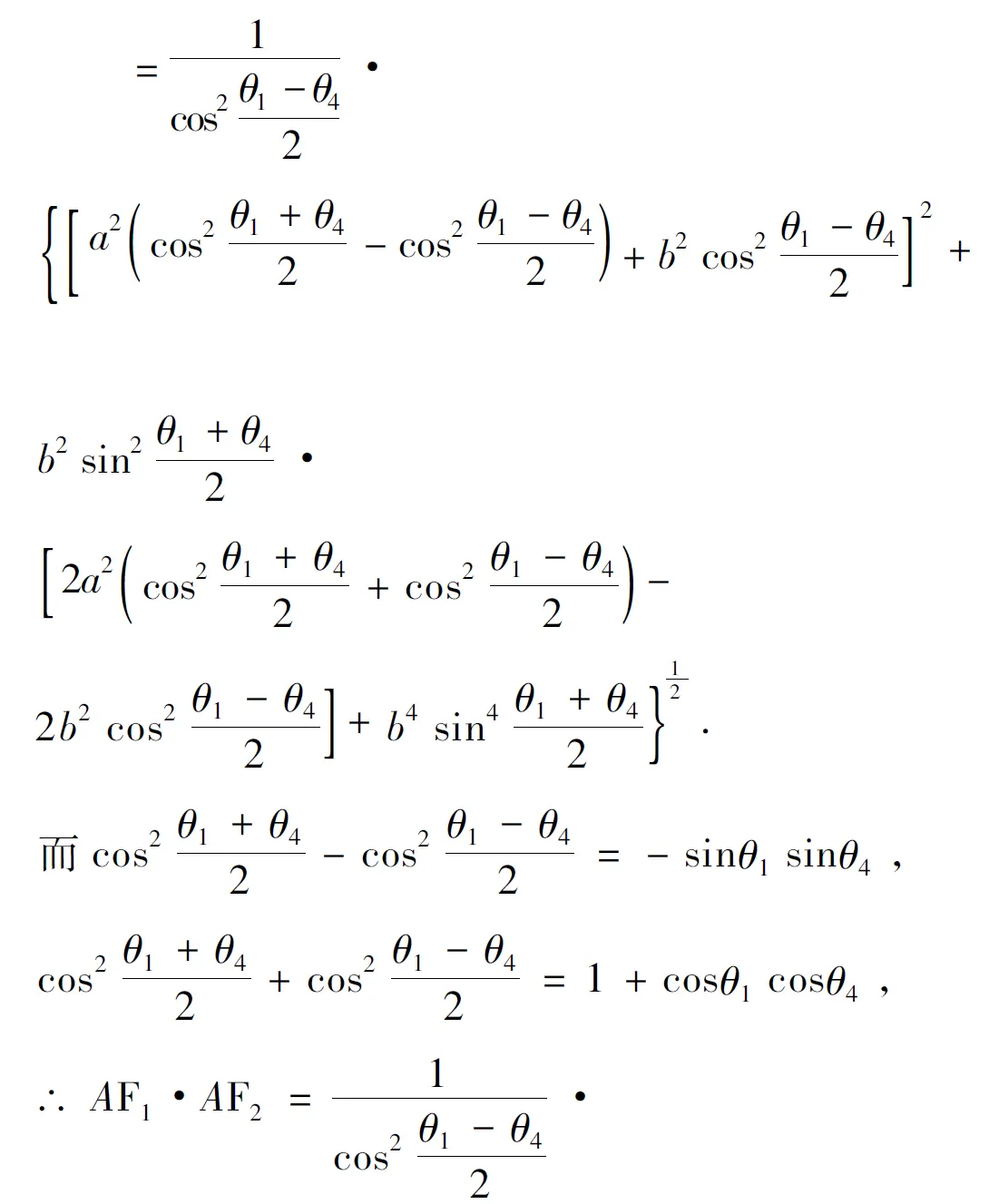
(4)

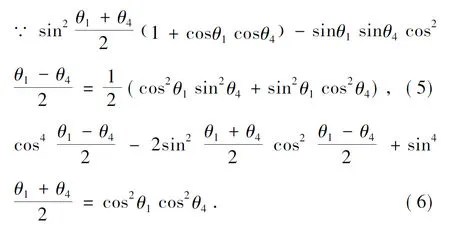
(5)、(6)代入(4) 得,

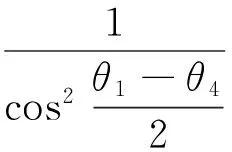
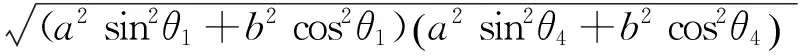
(7)

由(3), (7)得

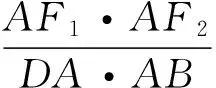
(8)

同理，

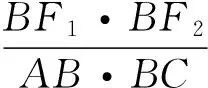
(9)

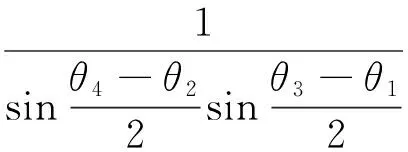
已证命题成立.

同理，也可证得：

定理 若△ABC是椭圆L的外切三角形，F1，F2是椭圆L的两个焦点，则

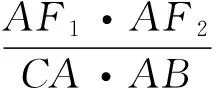
(责任编辑 张建军)

2014-05-05

朱华东，男，江苏如皋人，江苏省石庄高级中学教师，中教一级.

G632.3

A

1671-1696(2014)11-0093-04