热力学函数关系的简捷记忆法*

季 益 刚 郭 琦 方 艳 陶 泽 榕

(江苏第二师范学院生命科学与化学化工学院，江苏南京 210013)

热力学函数关系的简捷记忆法*

季 益 刚 郭 琦 方 艳 陶 泽 榕

(江苏第二师范学院生命科学与化学化工学院，江苏南京 210013)

物理化学学习过程中，尤其是在热力学第一定律和热力学第二定律的学习过程中，涉及到大量的物理知识和数学公式.靠学生死记硬背无疑极大地增加了学生的学习强度，且很容易记错.本文尝试通过一些技巧，降低学生在学习热力学过程中的记忆强度，使学生能够熟练掌握相关的知识要点，并能灵活地应用在解题过程和生产生活的实践中.

物理化学; 热力学; Maxwell关系式; 应用

物理化学是研究物质系统的化学行为的原理、规律和方法的学科.通过物理的理论和实验方法，同时灵活地运用数学的公式和推论来研究化学变化的本质与规律[1,2].相对于无机化学、有机化学、分析化学等先行课程来说，物理化学课程中有较多的公式，更为重要的是，很多的公式都有严格的使用条件.如何掌握这些公式并熟知它们的使用条件，是物理化学学习的难点也是重点.本文就热力学学习的一些心得，尤其是Maxwell关系式在热力学中的灵活运用作初步介绍.

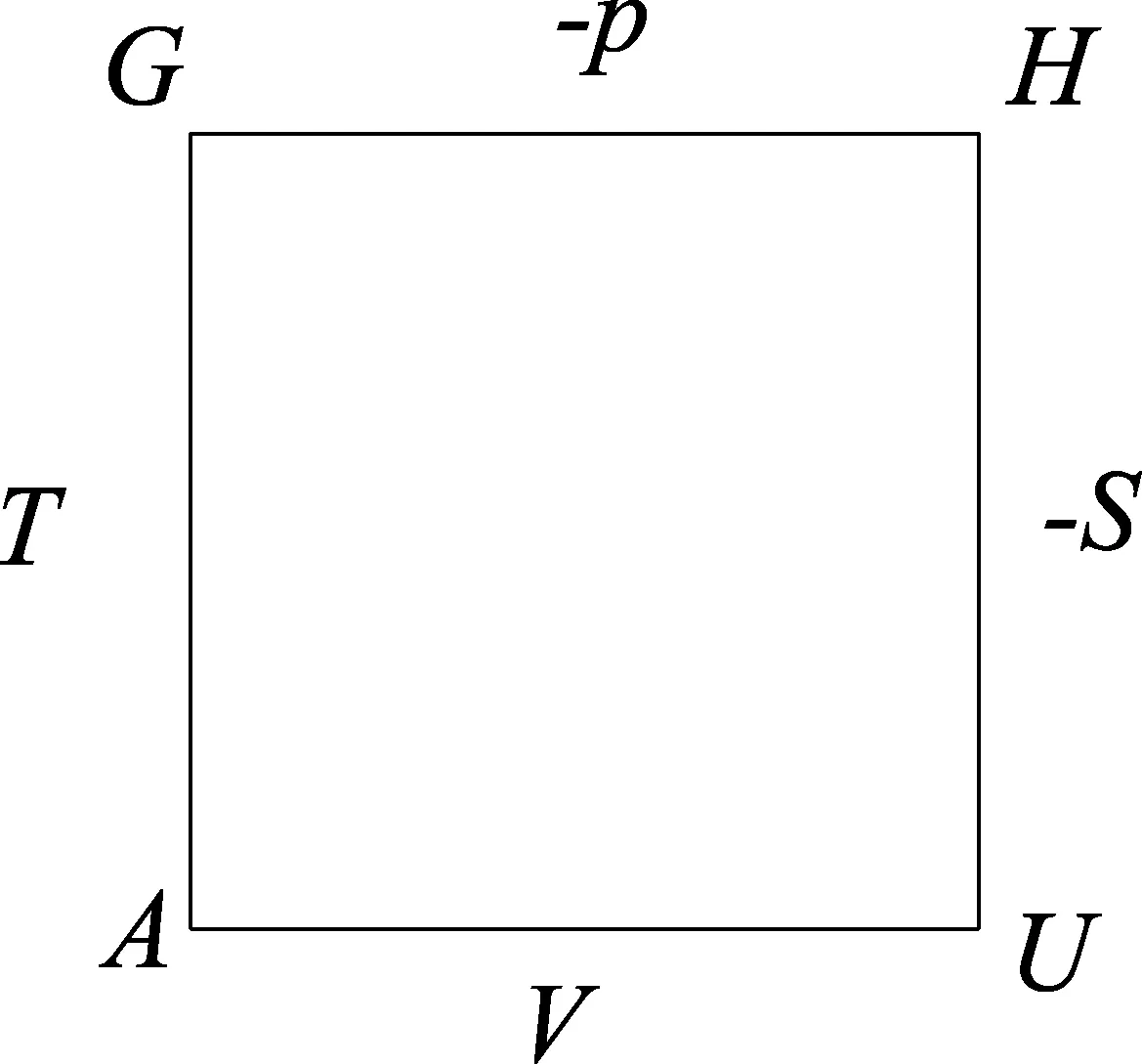
图1

物理化学的热力学主要包含的物理量包括：物质的量n、功W、热Q，热力学能U、焓H、熵S、Helmholtz自由能A、Gibbs自由能G,以及常见的物理量压力p、体积V、温度T.为了便于记忆，不少科研工作者作了归纳总结，下文提供一种便于记忆的方法，并结合笔者的一些心得，供初学者来学习和掌握[3～5].由于以下方法可以帮助初学者解决很多的问题，笔者将其称为“神奇的小方框”，将A、G、H、U(其顺序恰好为字母的先后顺序)按顺时针方向置于正方形的四个顶点处，将T、S、p、V按如图顺序置于A、G、H、U之间，即分布于正方形的四条边上，在p和S前加上负号，其示意图如图1所示.“神奇的小方框”用途可以概括为以下三大类.

1 应用于四个热力学函数A、G、H、U的关系的表达

A、G、H、U是热力学第一定律和热力学第二定律中四个重要的不可以通过实验直接测定的物理量，其量纲都是焦耳.它们的相互关系如公式1～4所示.在所有公式中p和V必然成对出现，T和S必然成对出现，这样方能保证其量纲为焦耳.这四个公式中的“+”和“-”是同学们容易记忆错误的部分.A、G、H、U这四个物理量可以用相邻的物理量来表示它.顶点处的一个函数(如焓H)等于其顺时针方向的顶点处的下一个能量函数(如热力学能U)加上U顺时针侧的特征变量V(连同其前面的正负号一起)再乘以与其成对出现的物理量p(不带正负号),即得公式H=U+Vp.同理，可以写出物理量H和G的关系，G=H+(-S)T，即公式2;U=A+TS，即公式3.

H=U+pV(1)；G=H-TS(2)

A=U-TS(3)；G=A+pV(4)

2 应用于特征变量的确定和组成不变的封闭系统且只有体积功时的四个热力学基本公式的推导

组成不变的封闭系统且只有体积功时的四个热力学基本公式包括：

dU=TdS-pdV(5)；dH=TdS+Vdp

(6)

dA=-SdT-pdV(7)；dG=-SdT+Vdp

(8)

由“神奇的小方框”可以很直观地看出四个能量函数的特征变量.顶点处物理量(如热力学能U)的特征变量为其相邻的两条边上的物理量S和V，可以表示为U(S,V)；同理，T和p为G的独立变量时，以G(T,p)表示.

U以S和V作为其特征变量，根据全微分的性质，dU=()dS+()dV,由于T和S必然成对出现，p和V必然成对出现,所以dS前面的括号内必然是T,dV前面的括号内必然是-p(必须带上物理量前面的正负号),即公式5，以此类推，可以很方便地写出公式6～8.

3 应用于Maxwell关系式的推导

Maxwell关系式可以由实验测定的偏微分来求算那些不易直接测定的偏微分.根据全微分的性质，由公式5～8可得常用的Maxwell关系式公式9～12：

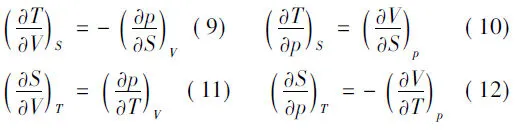
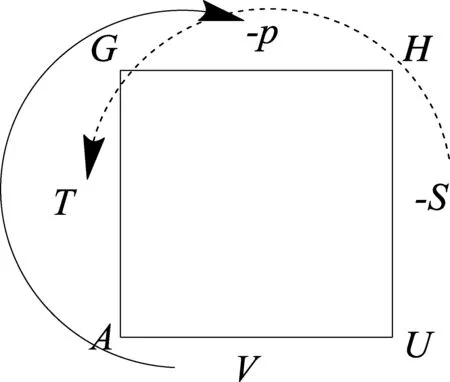
图2

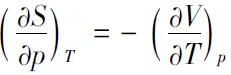
4 应用于其它重要公式的推导

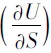
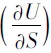
(13)

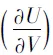
(14)

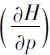
(15)

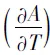
(16)

通过自身教学发现，使用该方法进行物理化学第一定律和第二定律的教学，有利于帮助学生轻松地记忆和灵活地运用物理化学关系式，摆脱枯燥无味、死记硬背公式的苦恼，从而提高学习积极性.

[1]傅献彩，沈文霞，姚天扬．物理化学[M]．北京:高等教育出版社，2005.

[2]朱志昂，阮文娟．物理化学[M]．北京:科学出版社，2008.

[3]陈桂芳，高之清，李胜利，等.麦克斯韦关系式的简捷记忆方法[J].广东化工，2011(2).

[4]吕申壮.热力学关系的图形记忆法[J].大学化学，2011(26).

[5]宋小利,李梅.热力学基本方程、对应系数关系式和麦克斯韦关系式的简捷记忆[J].榆林学院学报，2008(18).

(责任编辑 印亚静)

]江苏省高校自然科学研究面上项目“BINAM功能化的金属纳米粒子的制备及其在燃料电池中应用”(项目编号：14KJD150002)；江苏第二师范学院科学研究“十二五”规划课题“一种高效绿色贵金属纳米粒子的制备及其催化性能研究”(项目编号：JSNU-Y-4687)；江苏第二师范学院环境科技创新团队项目.

2014-08-28

季益刚，男，江苏盐城人，江苏第二师范学院生命科学与化学化工学院讲师，博士研究生.

G642.3

A

1671-1696(2014)11-0046-02

* [