棉织物悬垂系数与悬垂外观形貌外张及均匀程度的关系

莫振恩,佐同林,吴 薇,王子鹤

(内蒙古工业大学，内蒙古 呼和浩特 010051)

棉织物悬垂系数与悬垂外观形貌外张及均匀程度的关系

莫振恩,佐同林,吴 薇,王子鹤

(内蒙古工业大学，内蒙古 呼和浩特 010051)

文章对棉织物悬垂系数F、波峰半径离散系数CVRc、波谷半径离散系数CVRt、波峰分布角离散系数CVα等指标进行了测试，采用数据拟合的方法得到了关系方程。

棉织物；悬垂系数；波峰；波谷

目前，关于织物悬垂的研究主要集中在以下方面：其一，测试织物的组织结构参数，分析其与悬垂性之间的关系，导出回归方程，从而进行悬垂预测[1-4]；其二，使用KES-FB或FAST系统测试织物的物理机械性能，分析其与织物悬垂性能(主要是悬垂系数)的关系[5-11]；其三，研究悬垂的新型测试技术及仪器开发[12-14]；其四，基于组织结构参数或物理机械性能，采用一定的数学模型对静态悬垂和动态悬垂的模拟和仿真[15-21]。关于织物悬垂系数与其外观形貌之间关系的研究还不多见。本文选用棉织物，测试其悬垂系数，以及反映悬垂外观形貌的波峰波谷外张、波峰分布均匀情况的相关指标，分析二者之间的关系，并进行科学论证。

1 实验

1.1 实验材料

选用29种棉织物，规格如表1所示，按国标要求裁剪制样。

1.2 实验方法

将织物平展在图1所示织物展开平台上，支撑圆盘以500 mm/min的速度慢慢升起到织物完全脱离织物展开平台为止，悬垂形成。

数码相机垂直采集悬垂图像，将悬垂图像导入Matlab环境，对其进行图像处理和计算，从而得到悬垂系数F、波峰半径离散系数CVRc、波谷半径离散系数CVRt、波峰分布角离散系数CVα。依照下文所述方法，进行统计分析。

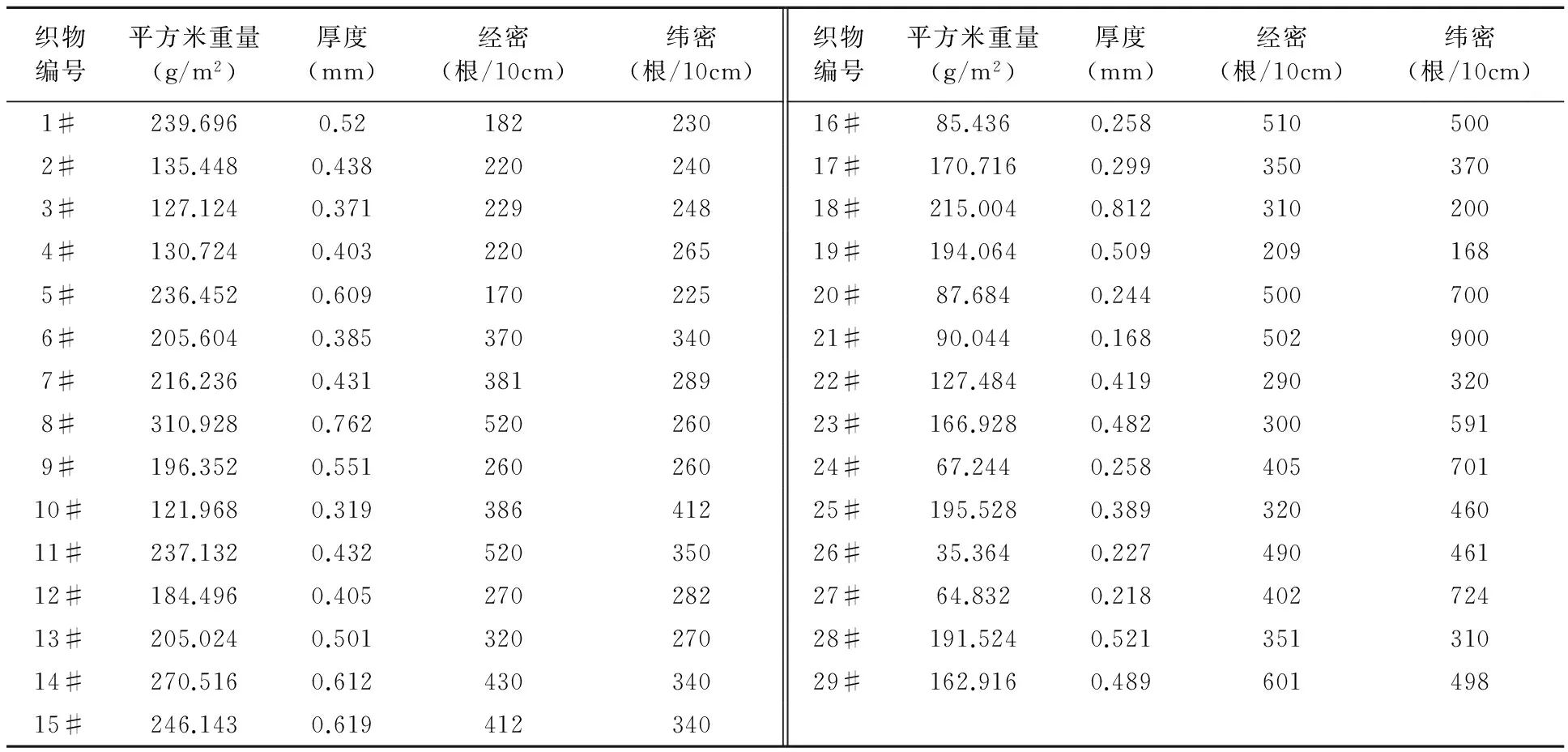
表1 选用织物的基本参数情况

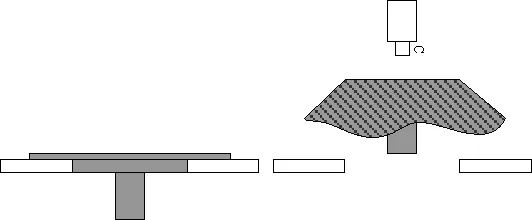
图1 织物展开平台

2 结果与讨论

2.1 波峰半径离散系数CVRc波谷半径离散系数CVRt

大量实验证明，对于悬垂系数小的织物，波峰半径均匀情况的感官冲击明显强于波谷半径，波谷半径分布往往不能引起注意，如图2所示。但是对于悬垂系数较大或各向异性较突出的织物则相反，波峰的外张程度基本很相近，波谷半径均匀情况的感官冲击明显增强，要优于波峰半径，这个时候，我们更关心波谷半径的情况，如图3所示。

图2 不同CVRc的织物悬垂效果图

图3 不同CVRt的织物悬垂效果图

对悬垂系数F和波峰半径离散系数CVRc、波谷半径离散系数CVRt在置信度95%下，分别按照式1、式2拟合，拟合曲线如图4、图5所示。拟合数据如表2、表3所示。

CVRc=A+B1×F+B2×F2

(1)

CVRt=A+B1×F+B2×F2+B3×F3

(2)

波峰半径离散系数CVRc、波谷半径离散系数CVRt和悬垂系数F的拟合曲线分别为f(F,CVRc)和f(F,CVRt)，二者的变化趋势明显不同；f(F,CVRc)整体趋势为递减，表明随着悬垂系数的增大织物越来越硬挺，导致各波峰张角变化趋于一致，则波峰半径的离散越来越小；f(F,CVRt)先递增后又缓慢递减，在F∈(10%,30%)时，CVRt单调递增明显，说明波谷的外张能力有所变化且逐渐加强，在F∈(30%,100%)时，CVRt缓慢递减，波谷张角变化趋于一致。

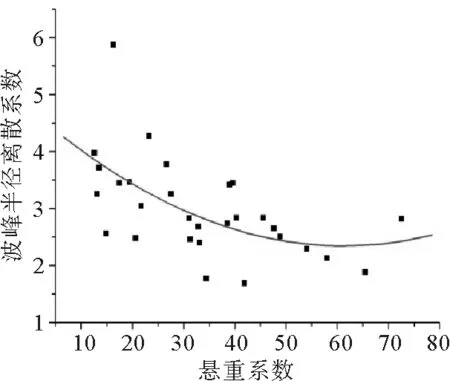
图4 CVRc和F的拟合曲线图

图5 CVRt和F的拟合曲线图

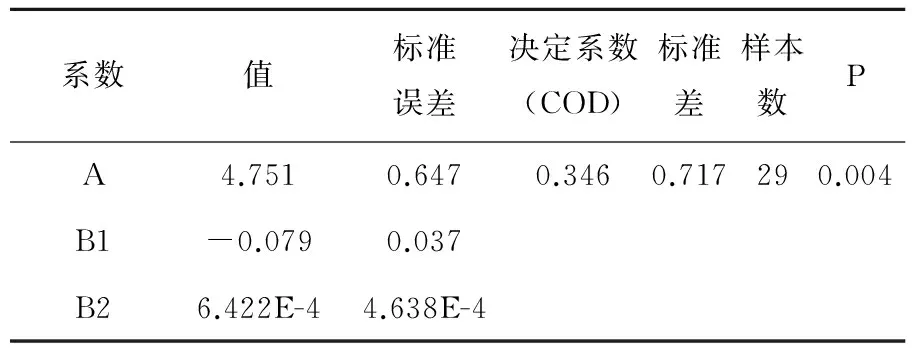
系数值标准误差决定系数(COD)标准差样本数PA4.7510.6470.3460.717290.004B1-0.0790.037B26.422E-44.638E-4

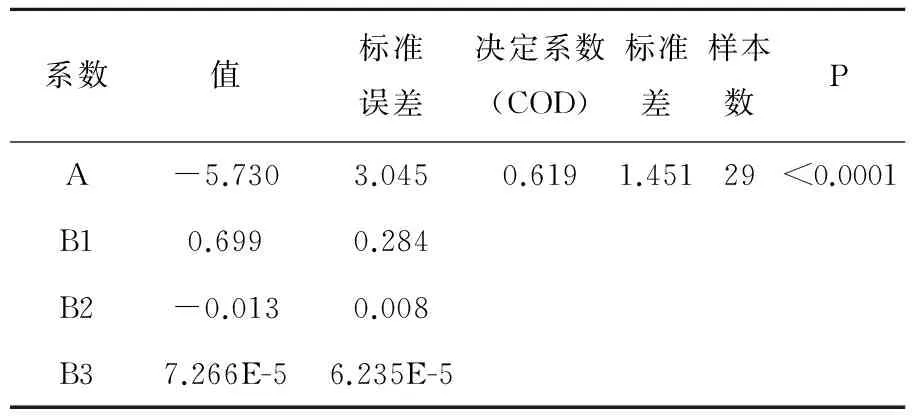
表3 CVRt和F拟合相关数据表

曲线f(F,CVRc)的决定系数为0.346，拟合效果一般，但曲线整体呈先递减后一致的趋势变化较为明显。曲线f(F,CVRt)的决定系数为0.619，拟合效果一般，但曲线整体呈先递增后一致的趋势变化较为明显。

2.2 波峰分布角离散系数CVα

大量的试验证明，波峰分布角是否均匀，即离散较小，对于悬垂外观的影响非常显著，其对人眼的感官冲击要强于波峰半径和波谷半径是否均匀所造成的视觉效果，如图6所示。

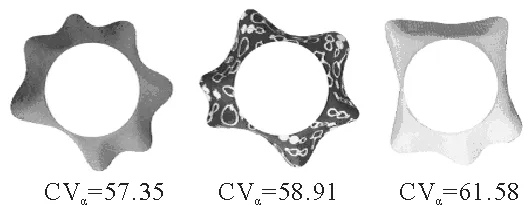
图6 不同波峰分布角离散系数的织物悬垂效果图

对悬垂系数F和波峰分布角离散系数CVα在置信度95%下，按照式3拟合，拟合曲线如图7所示。拟合数据如表4所示。

CVα=A+B1×F+B2×F2+B3×F3

(3)

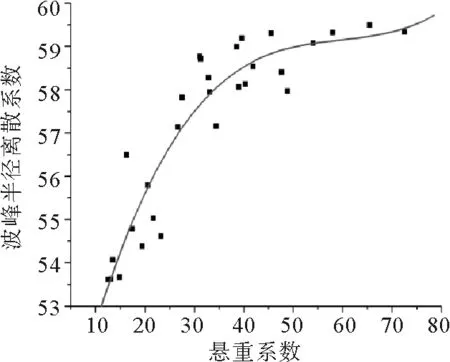
图7 CVα和F的拟合曲线图

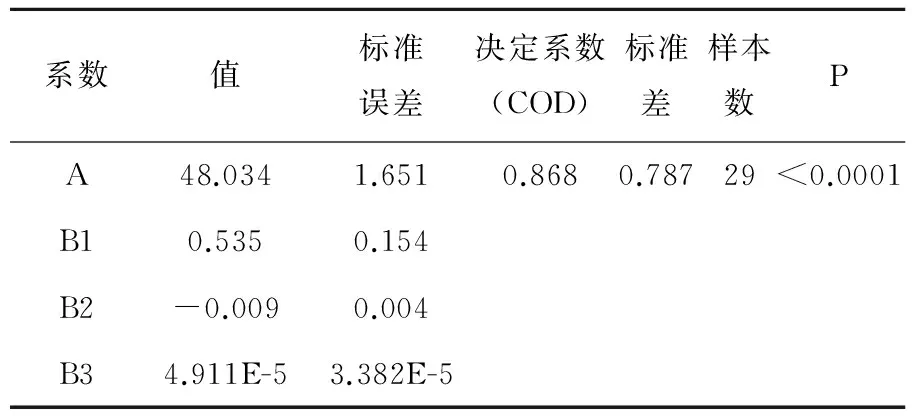
系数值标准误差决定系数(COD)标准差样本数PA48.0341.6510.8680.78729<0.0001B10.5350.154B2-0.0090.004B34.911E-53.382E-5

波峰分布角离散系数CVα和悬垂系数F的拟合曲线为f(F,CVα)。f(F,CVα)单调递增，且先快后慢。随着悬垂系数F的增大，织物悬垂波峰分布越来越不均匀，在F∈(10%,35%)区间这种不匀变化较为明显，在F∈(35%,80%)区间，这种不匀变化较缓慢。

曲线f(F,CVα)的决定系数为0.868，拟合效果较好，曲线变化趋势明显。P值小于0.0001，说明式3非常显著。

3 结论

3.1 悬垂系数F小的织物，其波峰半径均匀情况对悬垂外观的影响明显强于波谷半径，波谷半径分布一般不能引起注意。对于悬垂系数F较大或各向异性较突出的织物，波峰外张程度基本相近，波谷半径均匀情况对悬垂外观的影响增强，且优于波峰半径。

3.2 波峰分布角对于悬垂外观的影响非常显著，其对织物悬垂外观的影响程度明显大于波峰半径和波谷半径。CVα和F的拟合曲线f(F,CVα)单调递增。在F∈(10%,35%)区间，CVα不匀变化较为明显；在F∈(35%,80%)区间，CVα不匀变化较缓慢。

3.3 CVRc、CVRt和F的拟合曲线f(F,CVRc)和f(F,CVRt)的变化趋势明显不同；f(F,CVRc)整体趋势为递减，随着F的增大织物越来越硬挺，导致各波峰张角变化趋于一致，波峰半径的离散越来越小。f(F,CVRt)先递增后又缓慢递减，在F∈(10%,30%)时，CVRt单调递增明显，说明波谷的外张能力有所变化且逐渐加强，在F∈(30%,100%)时，CVRt缓慢递减，波谷张角变化趋于一致。

[1] 许兰杰,李绍佳.织物的悬垂性能与其结构参数关系的探讨[J].辽宁丝绸,2013,(3):20—21.

[2] 荆妙蕾.轻薄型精纺毛织物的结构参数对其服用性能的影响[J].毛纺科技,2006,(5):48—51.

[3] 姜为青.薄型精纺毛织物悬垂性与结构参数的关系[J].纺织科技进展,2006,(4):69—70.

[4] 周华,邵琰芳,王春燕,温泉,周玲玲.涤纶织物性能指标与悬垂形态关系[J].纺织学报,2011,32(6):39—44.

[5] 任霞.毛精纺西服面料风格研究[D].郑州: 中原工学院,2011.

[6] 王建平.精纺毛织物风格综合评价与设计应用[D].苏州: 苏州大学,2006.

[7] 王春燕.精纺毛织物悬垂性研究[J].毛纺科技,2012,(3):58—91.

[8] 孙艳,杨建忠,郭娟琛.超细羊毛精纺毛织物动态悬垂性的研究[J].上海毛麻科技,2008,36(3):12—15.

[9] 张辉,朱华,张建春.织物弯曲、折皱和悬垂性能的比较研究[J].毛纺科技,2003,(3):58—61.

[10] 张辉,范立红,朱华.织物静态悬垂性能的分析[J].现代纺织技术,2003,11(1):3—7.

[11] 周玲玲.织物力学性能指标与悬垂形态关系研究[D].杭州: 浙江理工大学,2011.

[12] 匡才远,秦芳.织物悬垂性测试及模拟研究[J].广西轻工业,2010,(11):89—91.

[13] 齐红衢.织物悬垂测试及三维预测系统开发[D].杭州: 浙江理工大学,2011.

[14] 刘成霞,陈金芳.支撑台及试样形状对毛织物悬垂性的影响[J].毛纺科技,2012,(10):59—64.

[15] 师琅,孙润军.织物动态悬垂性的模拟研究[J].纺织科技进展,2012,(4):63—64.

[16] 沈毅,齐红衢.织物悬垂形态的模拟仿真[J].纺织学报,2010,31(10):34—39.

[17] 李翠玉,张义同,徐家福.机织物悬垂屈曲的数值模拟[J].天津大学学报,2007,40(1):46—50.

[18] 李翠玉,张义同,张小涛.基于MSC．Marc接口的机织物悬垂屈曲数值模拟[J].机械工程学报,2008,44(4):165—170.

[19] 徐军.织物悬垂性的数字化研究技术[J].青岛大学学报(工程技术版),2002,17(2):31—34.

[20] 王会岭.基于纱线及面料性能的织物动静态悬垂模拟[D].上海: 东华大学,2013.

[21] 谭凯协.织物悬垂性的计算机仿真研究[D].苏州: 苏州大学,2006.

[22] 佐同林.织物悬垂性能分析及评价体系的建立[D].上海:东华大学,2004.

Relationship between Drape Coefficient and Spread &Uniform in Drape Appearance of Cotton Fabric

MoZhenen,ZuoTonglin,WuWei,WangZihe

(Inner Mongolia University of Technology,Hohhot 010051, China)

Drape coefficient F, crest radius dispersion coefficient CVRc, trough radius dispersion coefficient CVRt,crest distribution angle dispersion coefficient CVαwere tested and analyzed. Relationship equation was obtained through data fitting method.

cotton fabric; drape coefficient; wave crests;wave troughs

2014-07-18

内蒙古自治区高等学校科学技术研究项目(项目编号：NJZC13127)

莫振恩(1986—)，男，广西南宁人，硕士研究生。

TS116

A

1009-3028(2014)06-0011-04