DS/FH 混合扩频测控系统中测量误差分析∗
鲍君海, 张晓林, 刘 佳, 周 波
(1北京航空航天大学电子信息工程学院 北京 100191 2西安卫星测控中心佳木斯测控站 佳木斯 154002 3航天恒星科技有限公司 北京 100086)
DS/FH 混合扩频测控系统中测量误差分析∗
鲍君海1, 张晓林1, 刘 佳2, 周 波3
(1北京航空航天大学电子信息工程学院 北京 100191 2西安卫星测控中心佳木斯测控站 佳木斯 154002 3航天恒星科技有限公司 北京 100086)
针对航天测控信号的高动态特点,介绍直扩/跳频(DS/FH)测控体制下应答机的结构原理,深入分析直扩/跳频测控应答机测量误差。着重讨论传输链路中大气延迟所引入的测量误差,并建立修正模型。所建立的修正模型和测量误差分析结果对DS/FH测控应答机设计实现具有重要意义。
DS/FH; 测控; 应答机误差; 大气延迟误差
引 言
直扩/跳频(DS/FH)测控体制兼有直接扩频系统的隐蔽性和跳频系统对干扰的躲避性,将DS/FH混合扩频测控体制应用到航天测控系统以提高抗干扰能力已成为一种趋势[1]。在航天测控系统中,伪码测距是直扩/跳频测控通信中一种重要的测距测速手段,它已经成为深空探测任务中测距体制的主要发展方向,我国的深空探测任务也将采用伪码测距体制[2],而应答机负责对测距伪码进行捕获跟踪和转发,配合地面测控站完成对目标速度和位置的测量,有着不可替代的作用。凭借航天器上安装的应答机,地面测控站可以实现对更远距离航天器,甚至具备隐身性能的航天器目标的测控。
相对于一般通信系统,测控系统需要进行高精度的测距测速,所以应答机带来的测量误差不可忽略。研究DS/FH混合扩频测控系统测量误差系统的设计与实现具有重要意义。文献[3]粗略地分析了伪码测距中的系统误差,但并不详细。文献[4]分析了星地伪码测距系统的实现结构,研究了系统中各误差源引入的随机误差和系统误差,但未详细分析电波大气折射误差。本文介绍了DS/FH测控系统方案中应答机的结构原理,并分析了应答机误差对测距测速的影响。由于大气层中的对流层和电离层对电波传播影响不可忽略,所以本文采用修正模型对其所带来的误差进行了修正。
1 DS/FH测控应答机结构原理
由于DS/FH测控信号的特殊性,应答机要完成对接收信号跳频图案、直扩伪码相位和载波频率的三维捕获,与传统的应答机有所区别。应答机主要工作模式有两种:相干转发模式和非相干转发模式。在相干转发模式下,应答机从接收的上行信号中提取同步时钟,完成对伪码的捕获跟踪和转发,而非相干转发模式则采用独立的时钟对伪码进行捕获跟踪,并且在对遥测信息进行处理后转发。这两种模式的测量误差基本相同,本文以后者为例,对测量误差进行分析。
DS/FH测控应答机工作原理如图1所示。
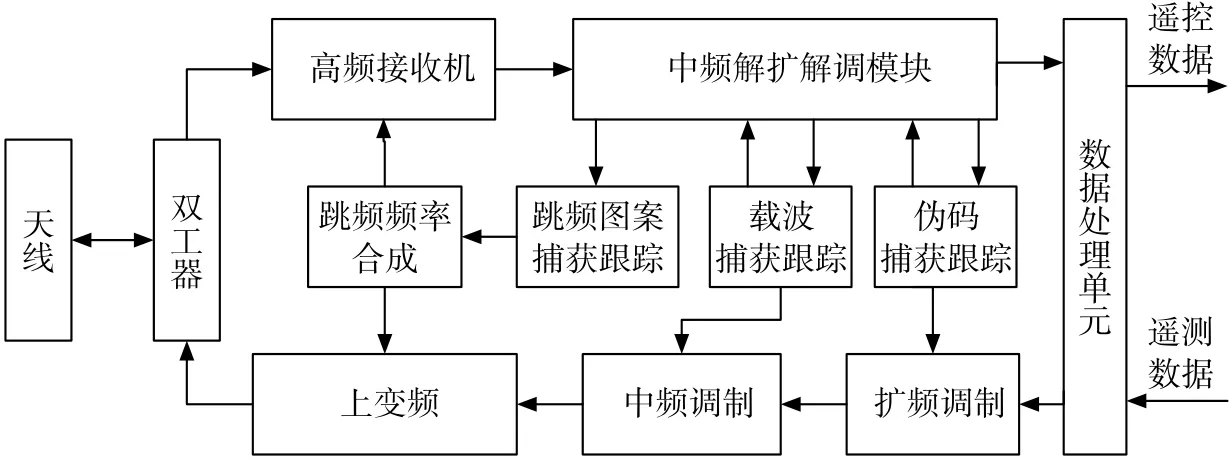
图1 DS/FH测控应答机工作原理
上行信号被应答机接收后,使星载本地跳频频率合成器工作在同步频率的快速扫描状态,直至完成跳频频率的识别,然后将上行信号转至中频。根据中频解扩解调模块解调出的同步信息完成跳频图案的跟踪,并且由载波捕获跟踪模块和伪码捕获跟踪模块完成直扩二维捕获跟踪。在完成对直扩/跳频测控信号的相干解调后,将解调出的遥控信号通过数据处理单元输出,同时,数据处理单元对遥控信息进行处理,利用本地时钟产生的伪码相位和地面测控设备中频频率比对完成上行链路距离和速度的解算。之后,数据处理单元将遥测数据、上行链路距离和速度测量值打包成帧,在利用本地时钟生成直接序列扩频码、中频调制载波频率和跳频图案后完成扩频调制、中频调制和跳频调制,并以一定的转发比通过发射机发射回地面测控站。
2 应答机测量误差
本文采用通常的收发码时延测量法。设航天器与地面测控站之间的距离为R,收、发测距信号的时延为τ,c为光速,可建立R与τ的关系:R=τc/2。
在影响测距精度的因素中,信号相位测量误差是最主要的误差,此外,DS/FH测控应答机计数器计数的系统误差和随机误差以及上行下行频率转发比等,都会影响测距精度[5,6]。
2.1 测距误差
2.1.1 设备时延零值误差
在连续波跟踪测量系统中,由于设备中存在惯性元件和尺寸误差,因此信号通过设备将产生固定时延,这个固定时延叫作设备时延(也称为距离零值)。设备时延值的测量误差和漂移误差直接影响系统测距精度,在系统测距误差中占有较大比重。传统的设备时延测量通常采用比对测量法。文献[7]中提出了一种尽量采用数字化、软件化计数的高精度距离零值测量系统的基本构成方法,此方法可以将应答机的零值误差维持在0.3m~0.5m的范围。
2.1.2 伪码跟踪环路误差
由图1可知,对接收到的信息要进行三维捕获跟踪,而应答机中码跟踪环路的主体为数字锁相环,由其引入的误差主要有:系统时钟漂移误差、多普勒频率引起的数字锁相环的环压波动误差、数字锁相环的热噪声引入误差、相位测量量化误差等。
①系统时钟漂移误差
当应答机工作在非相干模式下时,应答机和测控站的时钟独立,而前者系统时钟稳定度较差,故由应答机系统时钟漂移所引入的误差较大,不可忽略。对于二阶环,码钟的相位抖动为[3]:

式中,αA(τ)是闸门时间为τ的阿伦方差,fc为载波频率,BL为环路带宽。
当阿伦方差αA(0.05)=1×10-8、载波频率fc为2.3GHz、环路带宽BL为20Hz时,相位抖动估算为1. 656°。若伪码速率Rc为3MHz,则带来的测距误差为:

②多普勒频率引起的数字锁相环的环压波动误差
在高动态环境下,由于多普勒频移变化率较大,会引起伪码跟踪环的环压波动误差。由多普勒频移引起的非相干数字延迟锁相环(DLL)动态环压定义为[8]:

式中,Re以码片为单位,m为DLL环路阶数,这里取m=2,Rn是以码片来表示的测控站到航天器的距离,,取环路阻尼系数ζ=0.707。此时,DLL环压公式为:

式中,Δ·f /f为相对多普勒频移。当码片速率为3MHz、相对多普勒频移为6.9×10-7、环路带宽为6Hz时,由多普勒频率带来的DLL环压抖动为±4.79×10-9s,测距误差约为1.437m。
③数字锁相环的热噪声引入误差
热噪声又称白噪声,是由导体中电子的热震动引起的,存在于所有电子器件和传输介质中。热噪声的存在,会降低跟踪环路的性能,使输出相位产生抖动,从而影响测距精度。由热噪声引起的时延均方根误差为[3]:
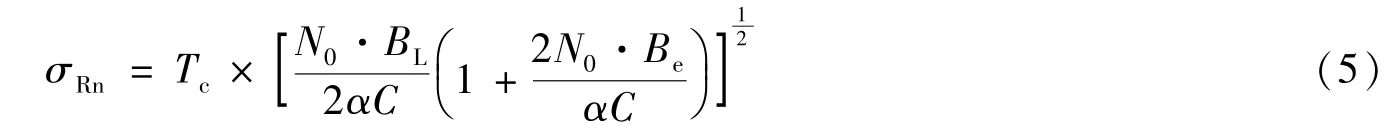
式中,Tc为伪码码片宽度,N0为高斯白噪声功率谱密度,α为损失因子,C为载波信号功率,Be为中频滤波器单边等效噪声带宽。
当伪码码片宽度为1/3×10-6s、信号载噪比C/N0=42.5 dBHz、损失因子为1、伪码跟踪环环路最优带宽为6Hz、中频滤波器单边等效噪声带宽为30kHz时,可得热噪声引入的误差为9ns,测距误差约为1.35m。
④相位测量量化误差
相位测量量化误差来自于直接数字频率合成器(DDS)。DDS原理框图如图2所示。
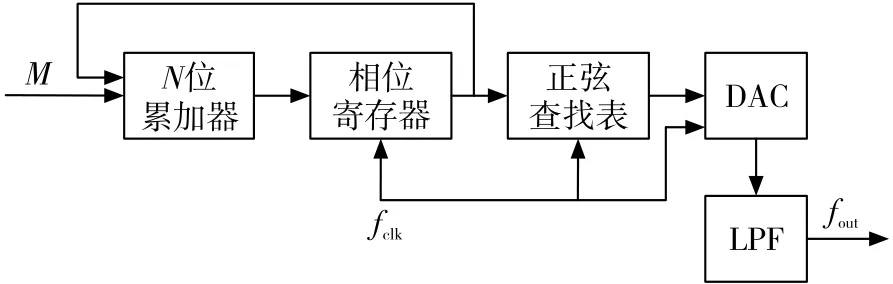
图2 DDS原理框图
DDS方程为:

式中,fout为输出频率,fclk为时钟,M为频率控制字,也叫相位增量,N为频率控制字的位数。当M=1时,DDS输出最低频率(也即频率分辨率)为fclk/2N。
当伪码速率为3MHz、频率控制字位数为32位时,相位测量量化所带来的测距误差为:
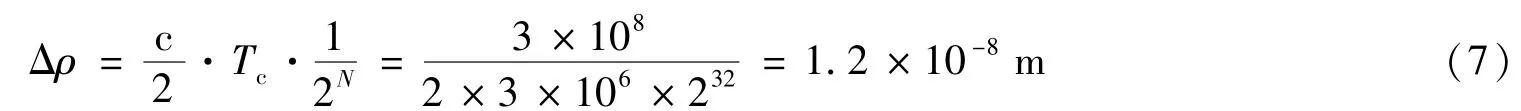
2.2 测速误差
2.2.1 应答机计数器误差
在非相干转发模式下,应答机测距测速原理如图3所示。
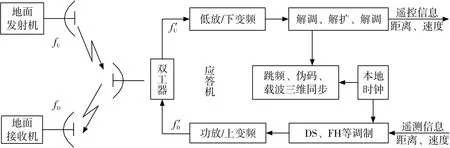
图3 应答机非相干转发测距测速原理
在非相干转发模式下,应答机测速模块在跳频图案、伪码相位和载波频率三维同步的基础上,利用载波捕获跟踪环路和跳频图案跟踪结果补偿修正多普勒频偏跳变,完成上行链路速度的解算。之后,将遥测数据、上行链路距离和速度测量值打包成帧后,在本地时钟的辅助下完成扩频调制、中频调制和跳频调制,并利用下行链路频段将其发射回地面测控站。目标测速估算公式如下:
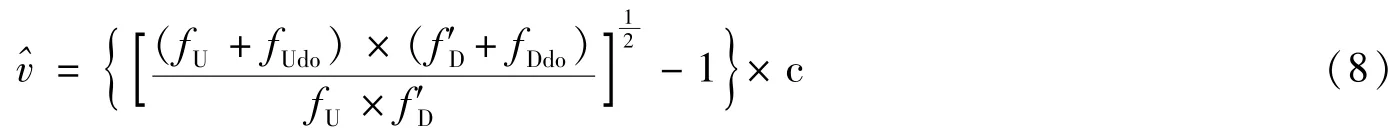
式中,fU、fD分别为地面发射频率和接收频率,f′U、f′D分别为应答机的接收频率和发射频率,fUdo、fDdo分别为应答机解算出的上行多普勒频偏和地面接收机解算出的下行多普勒频偏。
由式(8)可知,在非相干转发模式下,系统测速精度主要由多普勒频率精度决定,而应答机计数器计数的系统误差和随机误差是影响多普勒频率精度的主要因素[5],其关系式如下:
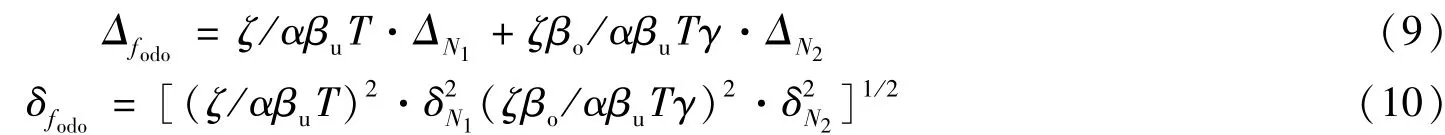
式中,Δfodo、δfodo分别为应答机本振的多普勒频率系统误差和随机误差,ΔN1、ΔN2和δN1、δN2分别为上行频率与本振频率加权差值计数器、本振频率计数器的系统误差和随机误差,T为计数器的计数时间,ζ为上下行频率转发比,α、βo、βu、γ均为常数,由系统决定。
当上下行频率转发比为240/221,T=10s,常数α、βo、βu、γ分别为221.5、2.03865、0.01、3时,地面测速误差可达0.124mm/s。可见,非相干测速精度并不比相干测速精度低。
2.2.2 应答机转发比引入的测速误差
由图1可知,当数据处理单元完成对遥控、遥测信息的处理后,要将其以一定的转发比通过发射机和天线发射回地面测控站。因此,应答机的转发频率精度会直接影响到地面测控系统的测距和测速精度[6]。转发比精度Δρ可表示为:

式中,n表示发射链路本振对基准时钟的倍频总次数。
当DDS时钟频率选择为100MHz,采用32位累加器,发射链路本振对基准时钟的倍频总次数为22.25时,转发比精度为0.518Hz,带来的理论测速误差为2.76×10-4mm/s。
3 大气层效应
大气层效应主要是指大气层中的对流层和电离层这两种特性不同媒质对无线电波传播速度和角度的影响。在统一测控体制下,测控站主要通过无线电波对航天器进行测控,所以有必要对大气层效应带来的测量误差做进一步的修正,以提高测量精度。
3.1 对流层延迟误差及其修正
对流层是高度为40km以下的大气层。电磁波通过对流层时,速度发生变化,引起传播延迟。这种延迟随对流层折射率变化,而折射率取决于当地的温度、压力和相对湿度。
对流层延迟由干延迟和湿延迟两部分组成。干延迟是指大气中的干燥气体引起的延迟,占总延迟的80%~90%;湿延迟则是由水蒸汽引起的,占总延迟的10%~20%。常用的对流层修正模型有霍普菲尔德(Hopfield)模型和萨斯塔莫宁(Saastamoinen)模型,本文采用霍普菲尔德(Hopfield)模型。其计算公式为[9]:
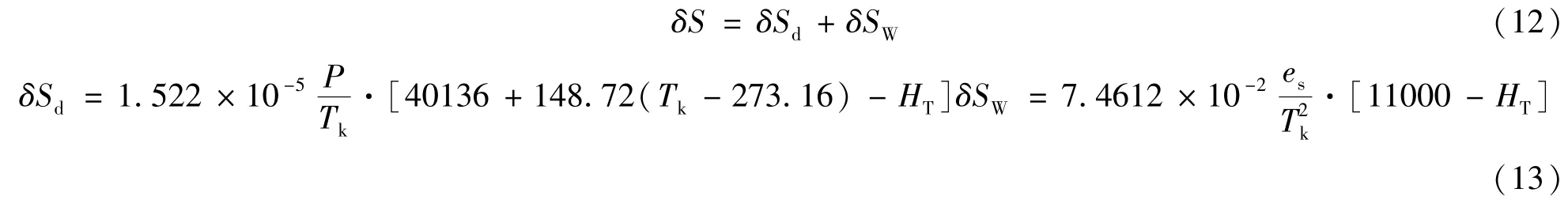
式中,δSd、δSW分别表示干延迟和湿延迟对电磁波传播路径的影响,P、es分别为测控站的大气压和水气压(单位:mbar),Tk为测控站的绝对温度(单位:K),HT为测控站的高程(单位:m)。
以海平面上的一组气象元素为例,大气压P=1013.25mbar,水气压es=11.691mbar,绝对温度Tk=288.15K,设高程HT=1km,则对流层延迟导致的测距误差约为2.319m。
3.2 电离层延迟误差及其修正
电离层是高度在50~1000km之间的大气层。受太阳辐射作用,电离层中的部分气体被分离,形成带正电的粒子和自由电子。电离层折射作用使入射波的相位传播速度(相速度)加快,而波内能量传播速度(群速度)减慢,即载波会产生一个相位超前量,而伪随机码调制信号会经历一个群延迟。群延迟和相位超前量都正比于电波传播路径上的电子总含量,两者大小相等,符号相反[10]。电离层引起的延迟误差为:
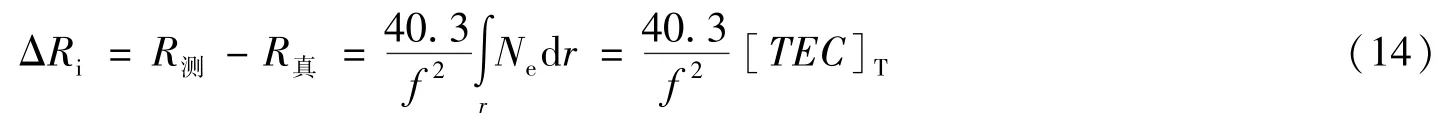
式中,f为电磁波的信号频率,[TEC]T表示总电子含量,它是沿卫星信号传播路径r对电子密度Ne进行积分后所获得的结果,即底面积为一个单位面积沿信号传播路径贯穿整个电离层的一个柱体中所含的电子数,其单位通常为电子数/m2或电子数/cm2。计算电离层延迟误差的主要困难在于难以准确计算出电子密度Ne,故需采用修正方法对[TEC]T进行修正,常用的修正方法有双频改正法、电离层模型改正法及差分改正法等,这里采用Klobuchar模型进行修正。
将整个电离层压缩为一个单层,称为中心电离层。该层距地面的高度一般为350km。设测控站到应答机方向的仰角为E,该方向与中心电离层的交点为k,对应观测时刻t,k的时角为t′,则电离层延迟改正为[11]
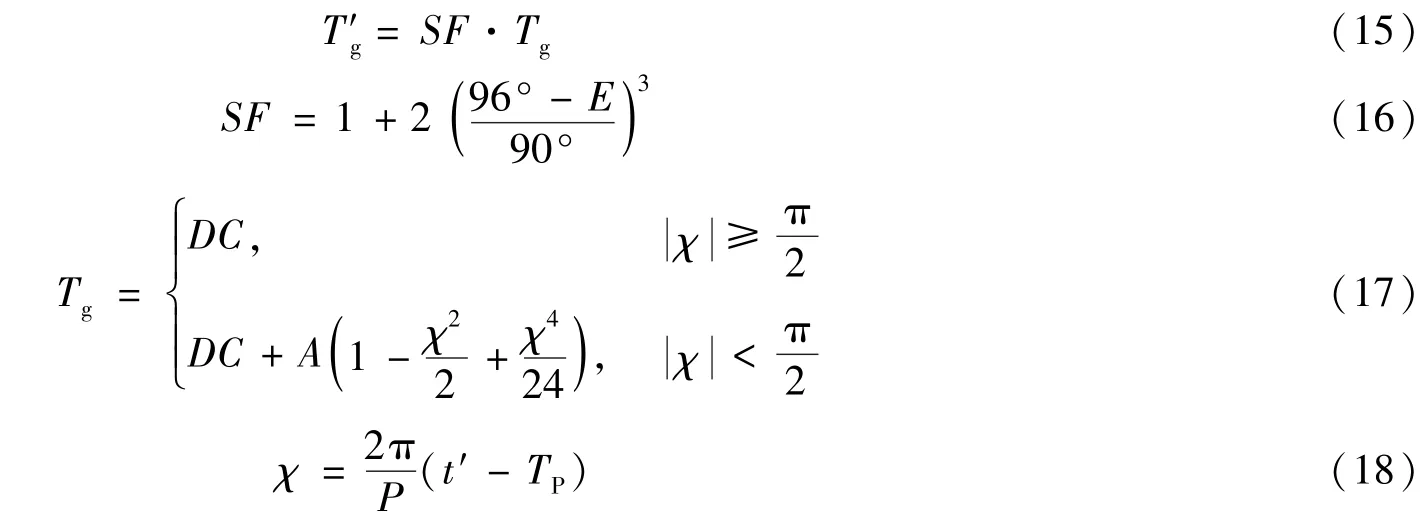
式中,DC为晚间电离层延迟,取5ns,A为电离层延迟函数振幅(单位:s),P为电离层延迟函数周期(单位:s),TP为最大电离层所对应的地方时,有TP=14h。电离层延迟修正模型是一种经验公式,用该模型公式进行修正,可消除60%左右的电离层延迟[11]。
4 测量总误差
当各个误差不相关时,总误差公式为:

式中,σi(i=1…n)为各个部分的误差。结合总误差公式和前面的分析可知,由应答机带来的测距误差约为2.025m。
在文中所给参数的情况下,由大气层引起的测量误差约为7.8m。
5 结束语
本文介绍了DS/FH测控体制下应答机的工作原理和测距测速的方法,并对应答机带来的测量误差进行了深入研究。本文还对大气层模型做了详细分析,针对大气层延迟带来的测量误差展开研究,并给出了修正模型。本文的测量误差分析对DS/FH测控应答机设计实现具有重要意义。
[1] 程乃平,潘点飞,郝建华,窦晓杰.DS/FH测控系统中的自适应波束形成算法研究[J].遥测遥控,2014,35(1):30~35.
[2] 丁溯泉,房鸿瑞.伪码测距在深空探测任务中的应用[J].遥测遥控,2012,33(3):1~5.
[3] 唐 军,谢澍霖,王卫星.航天扩频测控通信系统中伪码测距方法及精度分析[J].电讯技术,2006,46(4):92~95.
[4] 王 琦,吴 斌.航天测控系统中伪码测距精度分析[J].无线电工程,2009,39(1):40~44.
[5] 翟政安.航天器的非相干高精度测速方法及实现[J].电讯技术,2005,45(2):87~88.
[6] 万永伦.应答机技术研究与展望[J].电讯技术,2009,49(6):103~105.
[7] 胡建平.提高应答机测距精度的环节与测量计数探讨[J].电讯技术,2003,43(1):15~20.
[8] 张岩奇.扩频测距技术的研究[D].哈尔滨理工大学硕士学位论文,2008.
[9] 陈 芳,高永梅,徐良骥,张 玉.GPS测量误差中关于对流层延迟的探讨[J].西部探矿工程,2005,17(3):26~27.
[10] 罗 力.电离层对GPS测量影响的理论与实践研究[J].江西理工大学学报,2009,30(1):73~74.
[11] 王飞行.AOS体制下测距方法的研究[D].国防科学技术大学硕士学位论文,2004.
2014年3月世界航天发射表
[据国防科技信息网2014年4月3日综合报道]2014年3月,世界各国共执行了5次航天发射,具体内容如下表所示:
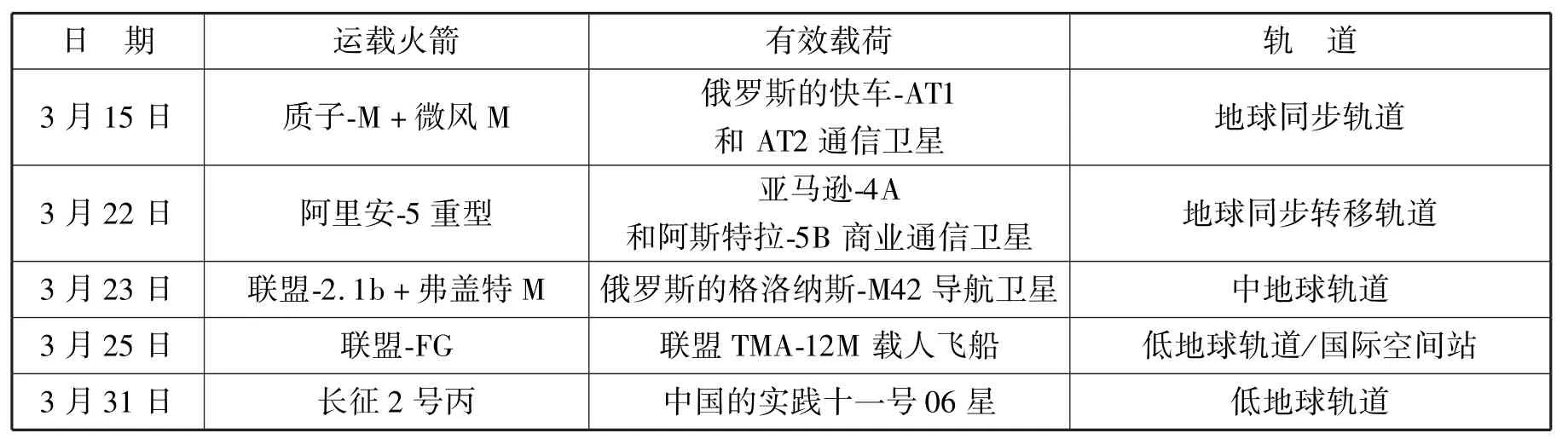
日 期运载火箭有效载荷轨 道3月15日质子-M+微风M俄罗斯的快车-AT1和AT2通信卫星地球同步轨道3月22日阿里安-5重型亚马逊-4A和阿斯特拉-5B商业通信卫星地球同步转移轨道3月23日联盟-2.1b+弗盖特M俄罗斯的格洛纳斯-M42导航卫星中地球轨道3月25日联盟-FG联盟TMA-12M载人飞船低地球轨道/国际空间站3月31日长征2号丙中国的实践十一号06星低地球轨道
(编辑部)
Error Analysis of Hybrid DS/FH TT&C System
Bao Junhai, Zhang Xiaolin, Liu Jia, Zhou Bo
The structure principle of hybrid DS/FH TT&C system is introduced according to the high dynamic aerospace TT&C signals.Themeasurementerrors of hybrid DS/FH TT&C transponder are analyzed in depth,in which themeasurementerror caused by atmospheric delay is discussed emphatically,and then themodified models for atmospheric delay are established.Themodified models and error analysis in this paper have important significance for the design and realization of hybrid DS/FH TT&C system.
DS/FH; TT&C; Transponder error; Atmospheric delay error
TN914.4
A
CN11-1780(2014)03-0007-06
鲍君海 1978年生,博士,主要研究方向为飞行器测控与网络信息传输。
张晓林 1951年生,博士,教授,主要研究方向为航空电子、测控通信、集成电路设计等。
刘 佳 1986年生,硕士,工程师,主要研究方向为航天器测控。
周 波 1985年生,硕士,工程师,主要研究方向为星载导航接收机等。
总装“十二五”预研重点项目(51306040401)
2014-01-10 收修改稿日期:2014-02-24

