并行组合扩频组合伪码捕获算法研究∗
郭黎利, 刘佳鑫, 李北明, 张文超
(哈尔滨工程大学信息与通信工程学院 哈尔滨 150001)
并行组合扩频组合伪码捕获算法研究∗
郭黎利, 刘佳鑫, 李北明, 张文超
(哈尔滨工程大学信息与通信工程学院 哈尔滨 150001)
为提高并行组合扩频测控通信系统接收端的同步性能,研究并行组合伪码的同步头、滑动相关、数字匹配滤波捕获算法,提出了并行组合伪码的FFT捕获算法。经理论分析与仿真验证,得出了数字匹配滤波与FFT捕获算法适用于并行组合扩频测控通信系统的结论。
并行组合扩频; 组合伪码; 同步捕获; FFT
引 言
并行组合扩频通信是一种有着较高频带利用率的扩频通信方式,它在带来通信效率提升的同时继承了传统扩频技术抗干扰、低截获概率、良好的多址通信能力等优势,有着广泛的应用前景[1,2]。由于并行组合扩频系统采用多伪码叠加传输,因此伪码的捕获需要解决计算量与伪码间互相关干扰等问题,这也是系统设计的难点,我们有必要研究一种符合组合伪码特性的捕获方式。
本文在分析组合伪码捕获特性的基础上,研究了可行的自同步、滑动相关、数字匹配滤波、FFT快速捕获共四种捕获方案,并将捕获算法应用于系统中,通过软件仿真对各种捕获算法作分析比较,验证了捕获方案的可行性,指出其各自的优缺点,同时还讨论了组合参数对捕获概率的影响。
1 并行组合扩频通信系统模型
并行组合扩频通信系统的特点在于多伪码序列传输。从M条序列中对应选取r条映射作为组合序列发送,即有种选择状态,相应信息量为log2比特[3];且r条序列的每条序列都可以有两种极性,则共有2r种极性状态,对应的信息量为r比特。相应的总信息量k为:

系统发射端将数据信息{d1,d2,…,dk}k比特送入串-并转换器,然后送入数据-序列映射器,按照数据映射算法对应后,从M条序列长度为L的扩频伪码{PNi}(i=1,2,…,M)中选取r条不同的序列,同时考虑序列的极性qi∈(0,-1,+1),(i=1,2,…,M),将r条并行序列中对应码片等幅度叠加,得到并行组合序列:

其中,j=1,2,…,N;qi为序列的选择控制因子,qi=±1表示在组合序列中选取了{PNi}或{PNi}的反极性序列,共有r个qi=±1的取值,qi=0则表示组合序列中未选取{PNi}。
设序列{PNi}的连续状态表示为PNi(t),则组合序列的连续状态在时域上的表示为:

其中,T为扩频伪码序列的码片长度。设P表示载波功率,fC为调制载波频率,φ0为载波初始相位,则并行组合序列经过载波调制后,得到发送信号表示为:
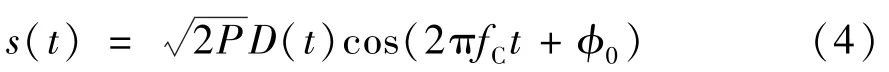

图1 并行组合扩频系统发射端结构
图1为并行组合扩频通信系统发射端结构。
组合序列在接收端与本地序列相关解扩之后,得到M个相关值,取其中绝对值最大的r个序列作为输出序列,依据数据-序列逆映射算法运算得到对应的本地序列序号,同时考虑到序列的极性信息,送入并串转换器,还原出发送信息[4]。图2为并行组合扩频系统接收端结构。
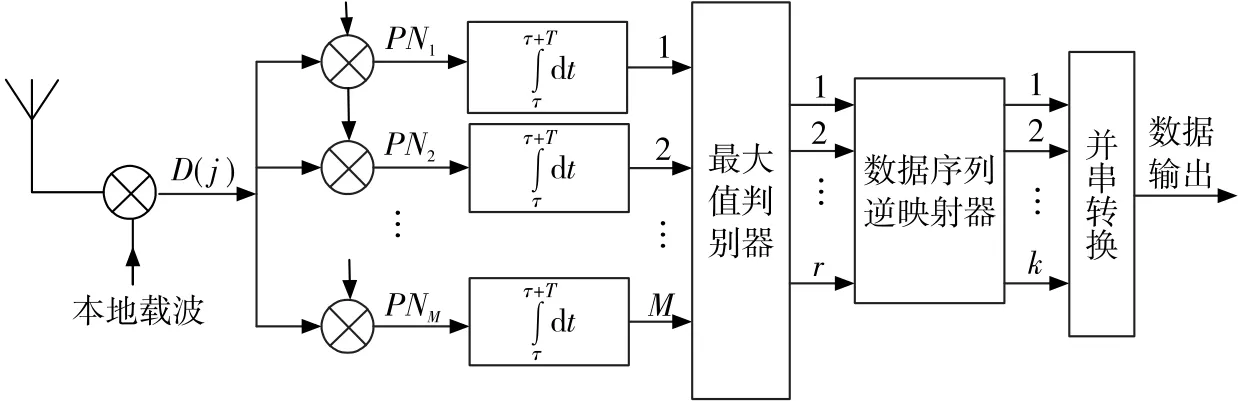
图2 并行组合扩频系统接收端结构
2 并行组合扩频组合伪码相关性分析
并行组合扩频系统发射端发送信号如式(4),假设通过加性高斯白噪声信道,在接收端基于软件无线电思想,中频采样信号为:

设TS=1/fS为码元采样周期,a(nTS)是均值为0、方差为σ2的高斯白噪声。
式(5)中D(nTS)表示组合伪码的采样,设M条伪码样本相互正交,在假定载波fC同步的情况下,M条本地已调序列可表示为与φ0相互独立的复指数型函数:

在直接扩频序列同步捕获中,伪码的捕获同步依靠伪码自身尖锐的自相关函数,而找到相应的码相位需求出两组序列的循环相关值再进行判别。在组合伪码中r条序列等幅叠加,理想情况下,对齐码相位时可以得到r个伪码各自的自相关函数最大值。但由于接收端并不确知传输伪码样本的伪码因子qi,因此找出最大自相关函数值需将组合伪码与样本M条本地伪码分别循环相关。
设所选伪码长度为L,本地伪码信息数据的采样点为N=LfS,M组本地伪码分别和接收的组合伪码进行N点循环相关,可以得到M×N阶相关矩阵。矩阵中M条行序列分别表示M条本地序列与组合伪码的相关函数值:

其中,m=0,1,…,N-1,i=1,2,…,M。信息部分为:

若本地序列PNi(t)伪码因子qi=±1,即参与组成组合伪码D(t),则有:

若本地序列PNi(t)伪码因子qi=0,即未参与组成组合伪码D(t),则

噪声部分表示为:

其中,RiN(m)均值为0,方差为Nσ2。
当PNi(t)参与构成组合序列D(t)时,相关后RiS(m)的概率密度应服从正态分布(qiN,Nσ2),M×N阶相关矩阵中共有r行服从此分布;而当PNi(t)不参与构成序列D(t)时,相关后RiN(m)概率密度服从正态分布(0,Nσ2),共有(M-r)行服从此分布。即码相位对齐时,r个伪码各自的自相关函数相关值存在于M组相关值中。
上述并行组合扩频通信系统须选择自相关、互相关性能良好的伪随机码,但实际存在的伪随机码无法实现以上分析的理想完全正交情况,故相关M×N阶矩阵中每行的循环相关值都存在伪码代数和自相关旁瓣的影响,每列都存在(M-r)行伪码间互相关值的干扰,若能减少这些影响,则可实现伪码相位的最大概率估计。
根据以上分析,给出组合伪码捕获原则:组合伪码需与M条本地样本伪码分别作相关运算;每个采样点循环相关得到M组代数和绝对值,选取其中最大的r组相加作为捕获备选峰值,尽量消除伪码互相关性对判决的干扰。
3 并行组合扩频伪码捕获方式
由于并行组合扩频系统多序列调制的特点,区别于直接扩频序列伪码的捕获,组合伪码的捕获需要与M条本地样本伪码分别作循环相关,捕获算法运算量成倍提高,多伪码间的非正交性也对伪码的捕获带来新挑战。结合上节对组合伪码捕获相关特性的分析,本节提出四种适合并行组合扩频系统的伪码捕获算法。
3.1 同步头捕获法
为规避组合伪码特性所带来的大运算量问题,可采用同步头捕获法来实现扩频伪码同步。该方法实现简单,且不会有组合序列自同步捕获所带来的大运算量。采用同步头捕获法,捕获的时间与运算量取决于同步头的长度。
然而,同步头方法更容易受到假相关的影响,且这种短码可能被有意地干扰或复制。此外,同步头还占用信息码元,会影响系统的传输效率[5]。
3.2 组合伪码最大值相加判决滑动相关捕获法
根据第2节对组合伪码相关性分析可知,要想实现组合伪码的捕获必须将其与M条本地序列分别循环相关。每个采样点循环相关得出M组相关代数和绝对值,选取其中最大的r组相加作为捕获备选峰值,并与门限值作比较。若峰值小于门限值,则调整时钟,滑动本地序列集的相位;若大于门限值,则判断捕获,返回组合伪码与本地伪码的相位差值。图3为组合伪码最大值相加判决滑动相关捕获法的原理框图。

图3 组合伪码滑动相关捕获法
3.3 组合伪码匹配滑动滤波器捕获法
前面讨论了适用于组合伪码捕获的滑动相关捕获方法,当伪码周期很长时,这种方法的捕获搜索时间也相应延长,影响系统性能。数字匹配滤波器法具有捕获时间短、数字实现容易和可编程能力强等特点,但对于并行组合扩频系统,组合序列的匹配滤波需要在系统单位时间间隔内处理大量的数据,造成系统复杂度的极大增加。
3.4 组合伪码FFT捕获算法
由于组合伪码数倍于单伪码捕获的运算量,因此引入FFT捕获算法[6,7]。两信号相关函数R(m)=可以通过FFT变换得到:
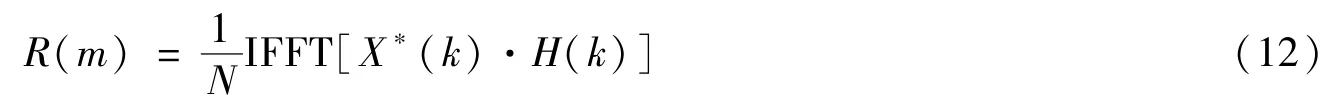
即通过两信号的FFT变换及其逆变换实现了信号的时域循环相关,式(12)中m=0,1,2,…,N-1;X(k)=FFT[x(n)],H(k)=FFT[h(n)]。
FFT算法应用在并行组合扩频系统中可以在一定程度上克服组合伪码捕获带来的大运算量问题,在可承受的运算量内实现对组合伪码的快速捕获。本系统采用平衡Gold码,码长为(2n-1),n为伪码的寄存器长度。
FFT模块的输入数据采样点数需恰好是2的整数次幂,但采样序列直接补零会造成自相关峰值的损失。对此,采用双倍长度补零法,即双倍扩展相关数据后补零,在相关运算量增加一倍的情况下,保证了相关峰值。
图4为应用于组合伪码序列的FFT捕获算法。如图所示,组合伪码分别与M条本地伪码进行周期内频域相关,依据第2节的捕获原则判断相关峰值。
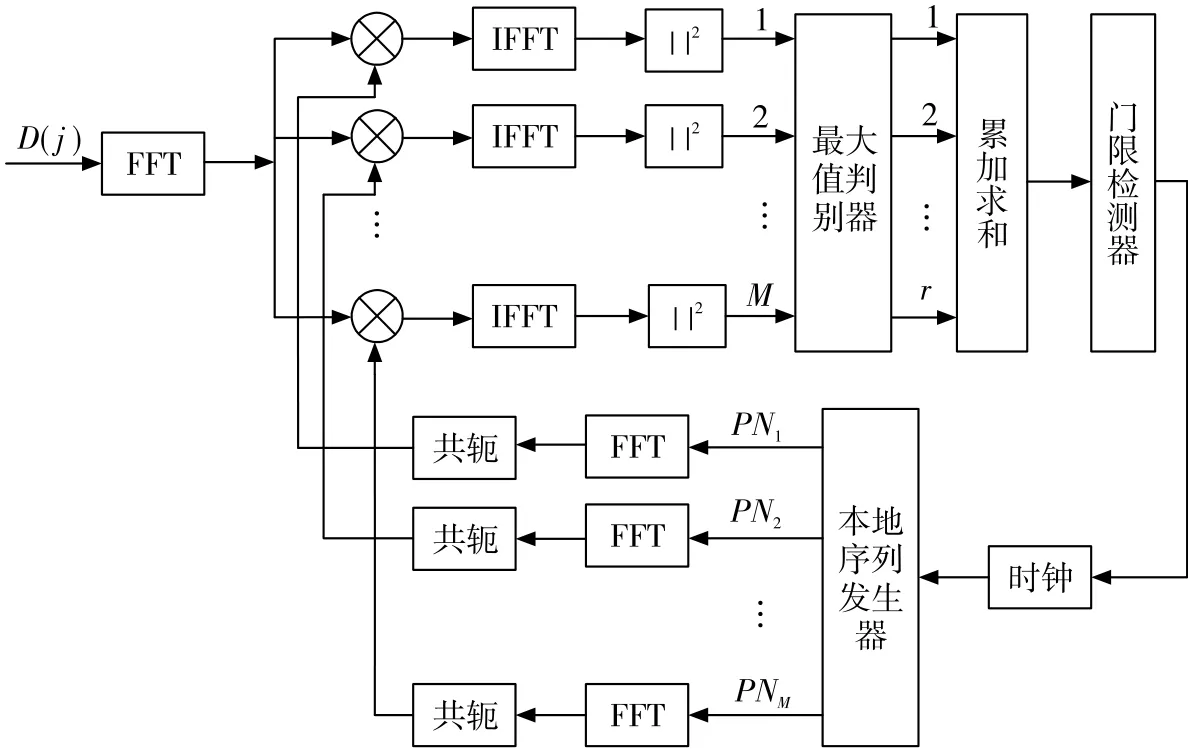
图4 组合伪码FFT快速捕获算法
4 捕获性能仿真
4.1 组合伪码捕获算法应用于并行组合扩频系统
建立并行组合扩频系统捕获仿真平台,四种组合伪码捕获方式捕获概率曲线如图5所示。

图5 组合伪码捕获概率曲线
仿真中M取值16,r取值为3;其中扩频序列选择周期长度为127的Gold序列,同步头选择周期长度为127的m序列;序列码元分辨率为TC/2。
由图可以观察,随着Eb/N0取值增加,四种捕获方式捕获概率相应提升,在大信噪比下,四种捕获方式均可以达到近似为1的正确捕获概率。在扩频调制序列与同步头序列码长相等时,组合伪码的三种自同步方式均优于同步头方式。其中匹配滤波算法、FFT捕获算法可以得到最优的捕获概率,两种捕获算法捕获概率曲线基本重合,Eb/N0取值8dB时,均可以将捕获差错率控制在0.2%内。在伪码码长较短时,滑动相关法与同步头法均不适宜在低信噪比下工作。

图6 并行组合扩频误比特率曲线
图6为接收端同步捕获后,由解扩还原数据得到的系统误比特率曲线。受捕获精度的影响,捕获算法误比特率曲线均差于理想情况(捕获概率为1)。Eb/N0取值8dB时,系统应用三种自同步捕获法得到的误比特率在10-3左右。在低信噪比下,匹配滤波捕获法与FFT捕获算法有着更高的通信可靠性。
由于组合伪码捕获代数和特性,对于相同的调制码长,并行组合扩频系统自同步捕获所需运算量至少是单一伪码调制伪码捕获运算量的M倍,M值较高时会极大地提升捕获运算量。数字匹配滤波捕获法较短的捕获时间是以在单位系统时间内处理大量信息得来的,而对于并行组合扩频系统,组合伪码的相关特性无疑会进一步对系统的数字匹配滤波提出更大的运算量要求,硬件设备要求也更高。
FFT捕获方式拥有与数字匹配滤波相似的捕获性能——短捕获时间,且相对于数字匹配滤波方式,其应用时频运算的转换在一定程度上减小了系统运算量。
设FFT捕获算法的平均运算量为O1,数字匹配滤波捕获算法的平均运算量为O2,则O2/O1代表了在相同条件下,两种捕获算法正确捕获的平均运算量比值,当比值大于1时,代表FFT算法相比匹配滤波算法有着更少的运算量。设扩频伪码码长为L,表1是不同伪码序列长度下,并行组合扩频系统组合伪码的数字匹配滤波与FFT捕获算法的运算量比值。随着L的增加,FFT捕获算法的运算量优势越来越明显。

表1 并行组合扩频系统捕获算法运算量比值
对于并行组合扩频系统组合伪码捕获所需的大计算量,FFT捕获方式无疑是一种更好的解决方案。
4.2 并行组合序列参数对捕获概率的影响
并行组合扩频系统扩频伪码M与r取值对捕获概率的影响如图7所示。仿真以FFT捕获算法为例,分两种情况进行讨论。
第一种情况:M一定,增大r。此时,随着r的增大,算法的捕获概率增大:
第二种情况:r一定,增大M。此时,随着M的增大,算法的捕获概率相应增加,但其概率密度增幅较第一种情况小。
此外,系统的复杂度和计算量随着M的增大而增加;而随着r的增加,系统复杂度和计算量变化不明显。通过以上讨论可以得出结论:增加r是提高系统捕获概率的一种有效方法。

图7 并行组合扩频系统模式参数对捕获概率的影响
5 结束语
本文分析了适用于并行组合扩频系统的组合伪码捕获特性,总结了组合伪码的捕获原则,并在此基础上讨论了四种组合伪码捕获方案。仿真分析结果显示,对于并行组合扩频系统组合伪码捕获所需的大计算量,FFT捕获方式是一种更好的解决方案。本文还讨论了并行组合伪码参数对捕获概率的影响,即捕获概率随着系统的伪码样本数量和映射伪码数量的增加而增大。
[1] Zhu Jinkang,MarubayashiG.Parallel Combinatory SSCommunication[J].IEICE Technical Report of Japan,1990,SSTA90(23):34~42.
[2] 朱近康.扩展频谱通信及应用[M].合肥:中国科技大学出版社,1993.
[3] 郭黎利,衣 强,李北明.基于r-组合的并行组合扩频通信研究[J].无线电通信技术,2007,33(4):25~27. [4] 李北明.并行组合扩频通信系统关键技术的研究[D].哈尔滨工程大学,2004:5~56.
[5] 曾兴雯,刘乃安,孙献璞.扩展频谱通信及其多址技术[M].西安:西安电子科技大学出版社,2004.
[6] Jing Xue,Qi Zhao,Wu Zhijie.An FFT-Based DS-SS Signal Acquisition Algorithm Research[C].Intelligent Information Hiding and Multimedia Sign,2008:1197~1200.
[7] 赵鹤群,杨家成.直接序列扩频通信中的FFT快速捕获方法[J].舰船电子工程,2013,(5):72~74.
声 明
为适应我国信息化建设,扩大本刊及作者学术交流渠道,本刊已被《中国科技论文与引文数据库(CSTPCD)》、《CNKI系列数据库》、《万方数据——数字化期刊群》收录,作者著作权使用费与本刊稿酬一次性给付。如作者不同意文章被收录上述数据库,请在来稿时声明,本刊将做适当处理。
《遥测遥控》编辑部
Research on Acquisition Algorithm of Combinatory Pseudo-random Codes in Parallel Combinatory Spread Spectrum System
Guo Lili, Liu Jiaxin, Li Beiming, Zhang Wenchao
In order to improve the synchronous performance of parallel combinatory spread spectrum communication system,the synchronization head,sliding correlation and digitalmatched filtering capture algorithms for combinatory pseudo-random codes are studied,and a Fast Fourier Transformation capture algorithm is put forward for combinatory pseudo-random codes.Through the theoretical analysis and computer simulation,the result is obtained that the digitalmatched filtering and FFT capture algorithms are applicable to the acquisition of combinatory pseudo-random codes in parallel combinatory spread spectrum communication system.
Parallel combinatory spread spectrum; Combinatory pseudo-random codes; Synchronization acquisition; FFT
TN911
A
CN11-1780(2014)03-0001-06
郭黎利 1955年生,博士,教授,主要研究方向为现代通信系统理论与技术。
刘佳鑫 1988年生,硕士,主要研究方向为宽带数字通信。
李北明 1976年生,博士,副教授,主要研究方向为宽带数字通信,高速数字信号处理。
张文超 1989年生,硕士,主要研究方向为宽带数字通信。
中国电子科技集团公司第五十四研究所并扩项目(KX132600013/ITD-U13006)
2013-12-30 收修改稿日期:2014-01-20

