基于多率信号处理的测控信号动态模拟方法

李 伟， 杨钏钏， 胡 凯

(1装备学院光电装备系 北京 101416 2西安电子科技大学电子工程学院 西安 710071)

基于多率信号处理的测控信号动态模拟方法

李 伟1， 杨钏钏2， 胡 凯1

(1装备学院光电装备系 北京 101416 2西安电子科技大学电子工程学院 西安 710071)

针对测控信号的大动态模拟问题，提出一种基于多率信号处理的动态模拟方法。该方法采用现有的存储延时方法对存储的静态测控信号实现整数倍采样间隔延时，并结合多率信号处理技术对整点延时后的信号实现小数采样间隔延时，有效地提高了动态模拟精度，解决了测控信号大动态高精度模拟问题。仿真分析表明，该方法能适用于不同体制测控信号的大动态高精度模拟，为测控设备动态性能测试过程中的动态模拟提供了一种实用方法。

多率信号处理； 动态模拟； 动态延时； 统一测控

引 言

在飞行器测控设备动态性能测试中，为检验飞行器应答机与地面测控设备间的匹配性等特性，需要对其进行对接试验，确保飞行器任务万无一失。对接试验中，动态性能测试是系统性能测试的一项重要指标，传统的动态性能测试通过飞机挂载应答机进行校飞试验，但由于飞机速度偏低等局限，导致校飞试验无法检测测控系统在高速运动状态下的动态性能[1]；另一种动态性能测试方法是基于硬件平台对存储的静态测控信号进行延时存储等处理，模拟飞行器在运动状态下的动态信号，但其只能实现整数采样周期的延时，模拟的动态精度较低。

为实现应答机和测控设备的动态性能检测，需对存储的中频数字静态测控信号加载动态信息，模拟动态测控信号。针对此应用，本文提出了一种基于多率信号处理的测控信号动态模拟方法，并对其进行了分析与仿真验证。结果表明，该方法能适应不同测控体制信号的大动态高精度模拟。

1 动态模拟方案

在理想情况下，飞行器或测控设备的接收信号Sr(t)与原发射信号Ss(t)的关系可表示为[2]：

其中，τ为信号传输延时，k为信号的幅度衰减。

由式(1)可知，模拟信号的动态主要就是模拟信号的功率(即幅度)变化和延时变化。功率变化主要与电磁波传播的距离和信道特性有关，在实际的模拟中可以采用功率衰减器实现[3]，其实现方法相对简单，因此本文重点讨论延时的模拟。值得注意的是，此处的延时信息中反映了飞行器与测控站间的距离信息、相对速度信息等，因此延时τ是时变的量。

传统的数字延时处理方法有存储器延时、计数器延时、数字时域内插、频域线性相位加权等，其中存储器延时方法实现过程较为简单，适用于不同格式信号的动态模拟，且能解决大延时问题，优点突出，其缺点是只能实现整数倍采样间隔的延时处理，模拟的延时精度较低。考虑到多率信号处理中的内插能够提高数据率[4]，降低最小延时间隔，从而可以提高延时模拟精度，因此本文结合内插抽取与存储延时对测控信号实现高精度动态模拟。

基于多率信号处理的动态信号模拟总体实现方案如图1所示。

图1 基于多率信号处理的动态信号模拟方案

假设原始信号A的数字化形式为Sr(nTs)，其中

式中，fs为中频信号采样频率，Ts为采样周期，n对应为不同时刻的存储地址，表示向下取整。对原数据进行I倍内插、滤波处理后得到信号B，信号B的数据率为信号A的I倍，相应的存储地址n′及其对应的延时M′可写为

假设存储器从首地址(n′＝0)开始存储信号B，进行动态模拟时，如果从与原存储地址相差M′个存储单元的地址(n′-M′)中读取信号B的数据，则相当于模拟了信号B被延迟M′个存储单元的延时，对每个时间点都重复上述过程，即可实现信号B的动态模拟，最后对所得数据进行I倍抽取，还原数据率，即可得到数据率为fs的动态信号C。

2 仿真验证

2.1 固定多普勒频率动态模拟仿真

为验证方案的可行性，对上述动态模拟方案进行仿真实验。仿真中假设飞行器与测控站的相对速度为固定值(vτ＝-8km/s)，根据相关知识可知，固定速度对应的多普勒频率为固定值，对应的延时τ为线性变化，为对比加载前后的效果，仿真中设置τ从0开始线性变化。仿真得到的真实延时τ、不内插时模拟的延时τ(nτ·Ts)、内插10倍后模拟的延时τ(n′τ·T′s)与时间的关系如图2和图3所示。

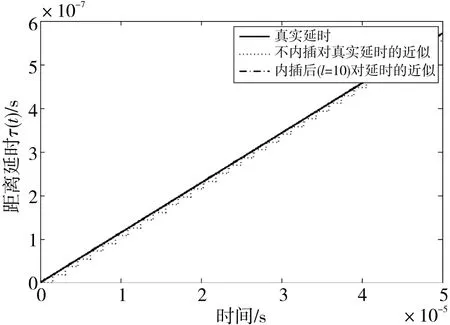
图2 距离延时的近似

从图2可以看出，内插后对各点加入的近似延时与真实延时的吻合程度较好。由图3可以看出，内插后对真实延时的近似效果比不内插要好，因此采用内插的方式模拟信号动态比直接模拟的精度高。

按上述方案对现广泛应用的标准TT＆C遥测信号、PCM_FM信号加入上述延时信息，仿真参数设置如表1所示。

表1 仿真参数

TT＆C信号和PCM_FM信号的动态模拟效果如图4和图5所示。仿真图中，标准动态信号是通过各信号的时域表达式直接生成，并以此信号作为判断动态信息加载效果好坏的基准。

图4 TT＆C信号动态模拟效果图

图5 PCM_FM信号动态模拟效果图

从上述动态模拟的时域效果图中可见，方案得到的动态信号与直接生成的动态信号基本一致。虽然无法从频域效果图中准确读出PCM_FM信号的频率偏移，但其频率偏移与模拟的动态信息(fd＝-800kHz)基本一致，从TT＆C信号的频域效果图可明显看出，动态信息加载后，信号中心频率发生了偏移，且与加载的多普勒频率信息一致(fd＝-800kHz)，由此证明前文所述方案能正确实现动态信息加载，且适应多种体制测控信号的动态模拟。

2.2 变化多普勒频率动态模拟仿真

为更加全面地考察方案的正确性，对加载变化多普勒频率信息的测控信号进行模拟仿真对比。在此只选择具有明显峰值频率的TT＆C信号进行仿真验证。假设飞行器的多普勒频率从零开始匀速变化，变化率为-200kHz/s，此处仍不考虑初始延时带来的影响。

按照方案对原始信号加入对应的延时后得到动态信号，并对每一段(1ms)动态数据进行FFT运算后求得动态信号的峰值频率，将其与原静态信号的峰值频率、理想的多普勒频率作对比，得到如图6所示的结果。

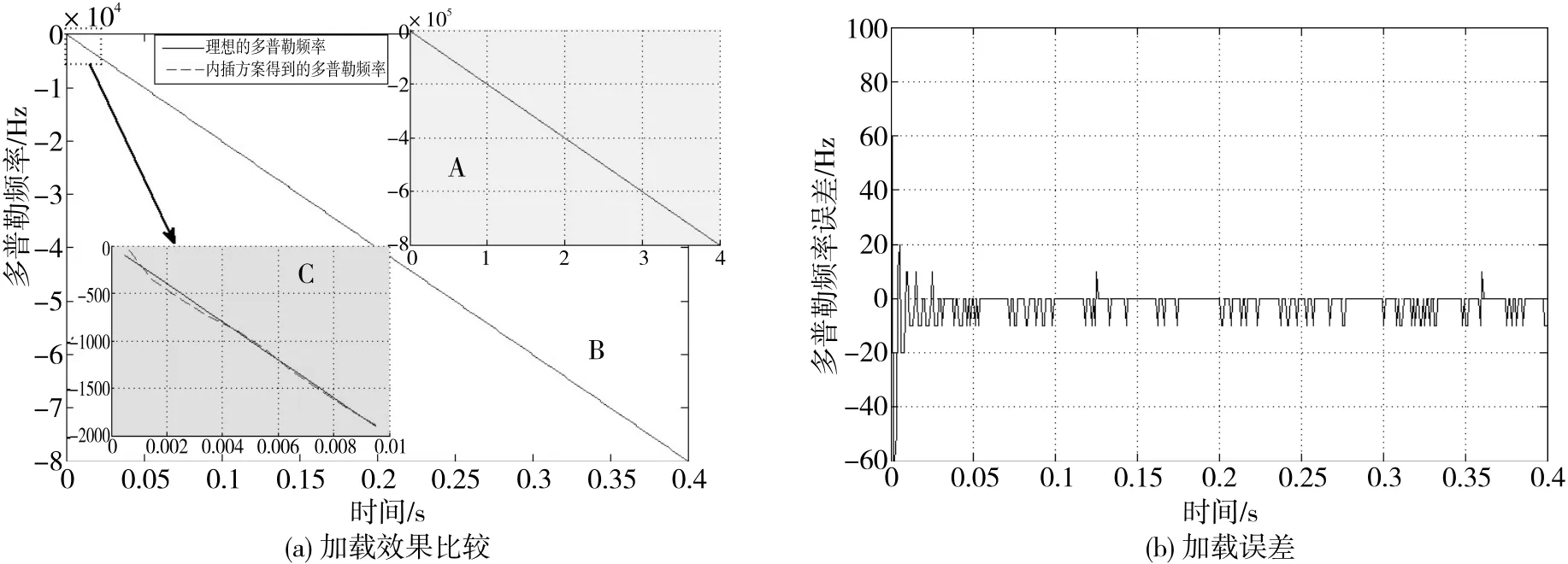
图6 TT＆C信号变化多普勒频率加载效果

图6(a)中，图A给出了0～4s内理想多普勒频率和方案加载动态后的多普勒频率对比效果，由于仿真时间较长，因此图A中的加载多普勒频率曲线是在100Hz频率分辨率下计算得到的。从图A中可以看出，模拟得到的多普勒频率与理想多普勒频率几乎一致。为更好地显示模拟效果，图B给出了0～0.4s的理想多普勒频率和动态模拟后的多普勒频率对比效果，模拟曲线是在10Hz频率分辨率下计算得到的。从局部放大图C中可以看出，动态模拟得到的多普勒频率与理想多普勒频率之间有一定的差距，但误差相对较小，且该误差随着时间的推移逐渐变小。

对模拟的多普勒频率信息作误差分析后得到图6(b)所示结果。从图中可以看出，在动态模拟开始时，多普勒频率信息误差比较大，但随着加载时间的增加，误差逐渐减小，最后稳定在10Hz以内，根据相应参数可计算出此时速度信息加载精度约为0.1m/s。

综合上述仿真结果可得出结论：采用多率信号处理方法对原信号进行延时，可正确地模拟测控信号的高动态特性。

3 精度分析

3.1距离信息加载精度

由动态模拟方案原理可知，使用前文所述方法模拟动态时，模拟的延时信息精度主要取决于数据率，内插倍数越高，则数据率越高，从而模拟的延时信息越精确[5]。

假设原始信号经I倍内插和滤波处理，则数据率变为原数据率的I倍，采样点之间的间隔变为原来的1/I，可实现的最小延时为原来的1/I，即

其中，ΔT′和ΔT分别为内插前、后的采样点间隔。

假设能根据轨道数据正确计算得到整点延时数n′τ，且采用四舍五入计算，则每个数据点的延时误差不超过半个采样间隔，并且模拟的延时是根据轨道数据独立计算，即前后数据点的延时误差不会发生积累，因此使用该方法模拟动态信号，其距离信息加载精度为

由上式可知，要通过该方法达到距离精度优于0.1m的要求，则需要内插倍数I取满足以下条件的整数

3.2 多普勒频率信息加载精度

根据频率与相位、时间的关系可知，接收信号瞬时相位φr为

其中，fRF为发射信号频率，φ0为发射信号初始相位。多普勒频率fd可写为

假设动态模拟的延时误差为Δτ，则接收信号的真实延时τ变为τ+Δτ，此时接收信号瞬时相位φ′r、多普勒频率f′d分别为

由于动态信息加载中加载的延时信息是在中频处理的，故上式中的fRF应改为中频频率f0，因此多普勒频率信息加载精度可表示为

将上述微分关系式转化为差分关系式可得

根据距离信息加载精度分析可知，动态信号任意两数据点之间的延时误差Δτ1-Δτ2不超过ΔT′，由此可得

综合上述结果，仿真得到多普勒频率信息加载误差与内插倍数的关系，如图7所示。仿真中假设信号中频频率为70MHz，内插倍数I为1～40，Δt取速度积分时间5ms和50ms。

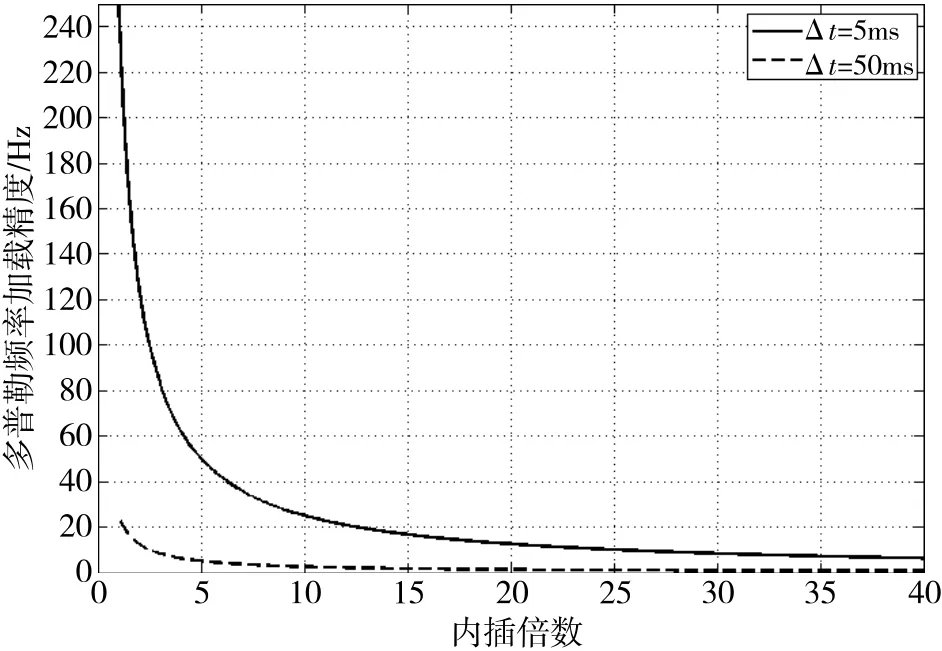
图7 多普勒频率加载精度与内插倍数的关系

从图7可以看出，多普勒频率信息加载精度取决于信息加载时间以及内插倍数。当内插倍数一定时，多普勒频率信息加载精度在短时间内比较低，但由于式(6)中的延时信息加载误差不会随时间积累，因此随着加载时间的延长，多普勒频率信息加载误差逐渐减小，精度相对提高，图6(b)的误差分析也证实了这一结论。当加载时间固定时，多普勒频率信息加载误差随内插倍数的增加而减小，多普勒频率信息加载精度相应提高。假设Δt按0.05s计算，ΔT′按满足0.1m的距离加载精度(I＝27)计算，求得多普勒频率信息加载精度Δf为0.93Hz，对应的速度信息加载精度为0.93×10-2m/s。

4 结束语

本文在传统存储延时实现动态模拟的基础上，结合多率信号处理理论，成功地实现了更高精度的测控信号大动态模拟，为测控设备动态性能测试中的动态信号模拟提供了一种有效的解决方案。仿真结果表明，本文方法能够较好地实现测控信号大动态模拟，其动态模拟精度主要取决于数字信号处理中的内插倍数，结果还表明，采用该方法模拟测控信号动态时，不需要限制原信号格式，相比传统解调模式的动态信号模拟[6]具有更好的适应性。

[1] 李润之.微波统一测控系统中RR·动态模拟[J].电讯技术，1996，36(5)：27～33.

[2] 丁鹭飞，耿富录.雷达原理[M].西安：西安电子科技大学出版社，2002.

[3] 邓永铭.采用开环模式实现深空动态模拟源设计[J].电讯技术，2009，49(7)：73～76.

[4] 杨小牛，楼才义，徐建良.软件无线电技术与应用[M].北京：北京理工大学出版社，2010.

[5] LakshmiS，JyothiC，Malinky G，etal.A Novel DDSUsing Nonlinear ROM Addressingwith Improved Compression Ratio and Quantization Noise[J].IEEE Trans Ultrasonic，Ferroelectries and Frequency Control，2006，53(2)：274～283.

[6] 兰宏志.测控信号的动态模拟[J].电讯技术，2012，52(6)：902～905.

俄罗斯“格洛纳斯”卫星导航系统出现故障

[据国防科技信息网2014年4月10日综合报道]据每日卫星新闻网站等多家媒体报道，2014年4月2日，由24颗“格洛纳斯”卫星组成的俄罗斯导航卫星系统出现故障，导致服务中断十几个小时。

据国外媒体报道，俄罗斯官方还未就此次格洛纳斯系统中断事件原因进行详细解释。从理论上分析，此次故障可归咎于系统故障、和/或软件升级故障、因近期太阳耀斑导致无线电通信中断、或者因赛博安全攻击所致。另外，有分析称此次故障可能是由于上载的星历表有问题导致。在2010年4月，美国的GPS系统中的一颗卫星曾在太阳耀斑发生后出现故障，不能执行指令。

不论由什么原因引起的，“格洛纳斯”卫星系统在中断近11～13个小时后才恢复。在此期间，故障影响到世界各地，尤其是专业应用领域，如农场的自动化拖拉机、采矿和重工业中的设备控制和机器人、国家基础设施领域勘测人员以及跨国工业等。

(编辑部)

Dynam ic Simulation of TT＆C Signal Based on M ultirate Signal Processing

LiWei， Yang Chuanchuan， Hu Kai

A processingmethod，based on multirate signal processing，is proposed to implement the high dynamic simulation of TT＆C signal.It implements the integer delay of the static data by store-delay，and implements the fraction delay bymultirate signal processing，which can improve the simulation accuracy effectively and solve the problem of high dynamic simulation of TT＆C signal. The simulation results show that the method is able to realize high accuracy and high dynamic simulation of TT＆C signals with differentmodulations.The method provides a good way for the dynamic simulation in the dynamic performance test of TT＆C equipment.

Multirate signal processing； Dynamic simulation； Dynamic delay； TT＆C

V556；TN914.42

A

CN11-1780(2014)03-0013-06

李 伟 1989年生，硕士，主要研究方向为航天测控、数字信号处理等。

杨钏钏 1988年生，硕士，主要研究方向为电子设计自动化、嵌入式技术等。

胡 凯 1989年生，硕士，主要研究方向为航天测控、数字信号处理等。

2014-02-19 收修改稿日期：2014-03-03