基于协同进化遗传算法的航班进港优化调度

张 勰，赵嶷飞，刘宏志

（中国民航大学天津市空管运行规划与安全技术重点实验室，天津300300）

基于协同进化遗传算法的航班进港优化调度

张 勰＊，赵嶷飞，刘宏志

（中国民航大学天津市空管运行规划与安全技术重点实验室，天津300300）

航班进港调度问题是一个典型的组合优化问题，具有多约束复杂特性.针对遗传算法求解航班进港调度问题时多约束难以处理、运算量大、易陷入局部最优的不足，本文应用协同进化思想，构建航班进港调度问题决策解种群和惩罚因子种群，通过种群间的竞争、协作改善算法性能；设计一种带约束处理的编码策略，将安全间隔约束纳入编码过程，降低了问题的约束复杂度，进而提出一种改进的协同进化遗传算法(Co-evolutionary Genetic Algorithm，CoGA)，并应用首都机场的实际运行数据进行了仿真.结果表明，本文方法能够有效处理航班进港调度问题中的大量约束，在优化效果与GA算法相当的情况下，有效降低了计算时间，克服了问题规模剧增导致的计算效率低下的难题.

航空运输；协同进化；遗传算法；航班进港调度；空中交通流量管理

1 引 言

空中交通流量管理是保障航空运输安全、高效、流畅运行的重要手段.航班进港调度作为空中交通流量管理的核心问题之一，其目的在于为机场附近等待降落的航班安排合理的着陆顺序和着陆时刻，在确保安全的前提下提高航班进港运行效率[1].

航班进港调度问题是一个典型的组合优化问题，具有多约束复杂特性，而优化调度中对算法实时性的要求使得该问题的求解难度进一步增加.目前实际运行中先到先服务方法应用最为广泛.虽然简单、易用且公平，但由于忽略了众多有用的信息与条件，导致先到先服务方法实际运行效率低、灵活性差.随着航空运输业的蓬勃发展，特别是进入21世纪以来，航班进港调度问题得到了越来越多各国学者的关注，纷纷开展相关研究[2-15].Coumba等提出了基于时间窗口的着陆航班调度方法[2]. Beasley等学者建立了航班进港调度问题的线性规划模型，提出了一种基于混合整数线性规划的树搜索算法以解决静态航班调度问题[3].也有学者采用分支界定法[4]、模糊规划方法[5]对该调度问题进行求解.Dear提出约束位置交换（Constrained Position Shifting,CPS）概念，规定优化前后单架航班在队列中的位置变动不能超过某一固定范围[6].CPS思想使得调度结果易于管制员操作，并可以缩小搜索空间，加快搜索速度.之后Balakrishnan等人建立了基于CPS的网络图，提出了一种动态规划算法，并采用实际运行数据进行了仿真，取得了较好的效果[7,8].朱星辉等构建了该问题的网络流模型，并采用约束编程方法对模型进行了求解[9].

航班进港调度问题是一个典型的NP-hard问题[10].线性规划算法缺乏全局搜索能力，很多情况下难以找到最优解[11].计算智能方法由于具备很强的全局寻优能力，近年来被广泛应用于解决航班进港调度问题[10-19].Ciesielski和Scerri采用标准遗传算法和带滑动窗的遗传算法求解动态航班调度问题[10,12].Pinol将散布算法和生态算法应用于解决多跑道航班调度问题[13].Zhan等学者提出了基于滚动时域控制思想的蚁群算法，该算法具有很强的全局搜索能力[14].王世东等将降落过程建模成单机多目标规划问题，并利用蚁群算法进行了求解[15].此外，模拟退火算法[16]、免疫粒子群算法[17]、Memetic算法[18]、人工鱼群算法[19]也被用于求解此问题.虽然计算智能方法相较线性规划方法拥有更佳的全局搜索性能，但航班进港调度问题对于算法实时性的要求很高，上述计算智能方法由于计算代价过大，特别是在机场高峰运行时段，往往无法在合理的时间范围内给出调度方案，因而需要改进算法性能，如结合启发式知识，提高计算效率，以更好地应对航班进港调度问题.

遗传算法是一种模拟生物自然进化过程与机制的智能计算方法，具有并行性、鲁棒性强等优点，已在自动控制、组合优化、图像处理、函数优化及生产调度问题等领域得到广泛应用.虽然较传统方法具有诸多优势，但标准遗传算法存在收敛速度慢、易早熟等不足，并且在处理约束优化问题时往往难以取得理想的效果[20].本文应用协同进化思想，构建航班进港调度问题决策解种群和惩罚因子种群，通过种群间的竞争、协作改善算法性能；设计一种带约束处理的编码策略，将安全间隔约束纳入编码过程，降低了问题的约束复杂度，进而提出一种改进的协同进化遗传算法(Co-evolutionary Genetic Algorithm，CoGA)来解决航班进港调度问题.

2 问题描述

航班进港调度是对机场附近临近降落的航班队列进行顺序和时间上的优化，从而得到高效的航班着陆次序与时刻，以达到减小飞行延误、提高跑道吞吐量和飞行安全的目的.调度过程需要考虑诸多限制因素，例如两架航班间的安全间隔取决于其相对位置及机型，不同的降落顺序将导致不同的运行成本.因此，航班进港调度问题可以描述为，对于准备在某一机场降落的航班集合与机场跑道集合，已知航班的预计降落时间、降落时间窗、机型等信息，在满足一系列约束的情况下给出一个合理的调度方案，该方案包括航班队列的降落顺序和每架航班的降落时间.显然，航班进港调度是一类大规模优化问题.

2.1 优化目标

安全运行的前提下，经济效益是航班进港调度中的重要考量因素.航班提前或者延误都会带来额外的开销，相等的时间提前量或延误量，由于机型或优先级别的不同，所造成的经济损失也不相同.为此，引入提前/延误代价系数和航班的优先级系数计算总损失，并将航班队列的总额外代价作为优化目标.对于航班集合F，有

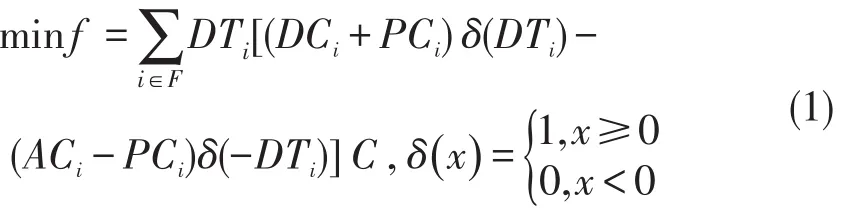
式中 DTi=STAi-ETAi为航班i的优化降落时间与预计降落时间之差，表示航班i优化前后的时间差；PCi表示航班i的优先级系数；ACi与DCi分别表示航班i提前代价系数与延误代价系数；C为单位延误成本.

2.2 约束条件

2.2.1 安全间隔约束

从空气动力学角度，所有飞机都会在其后部产生尾流.通常较大的机型所产生的尾流也较大，这对尾随飞行的飞机非常危险，甚至会导致飞行事故.因此，为保证飞行安全，任意两架飞机之间的时间间隔必须满足安全飞行需要的最低限度.国际民航组织对不同类型飞机间的最小尾流安全间隔做出了规定，如表1所示.

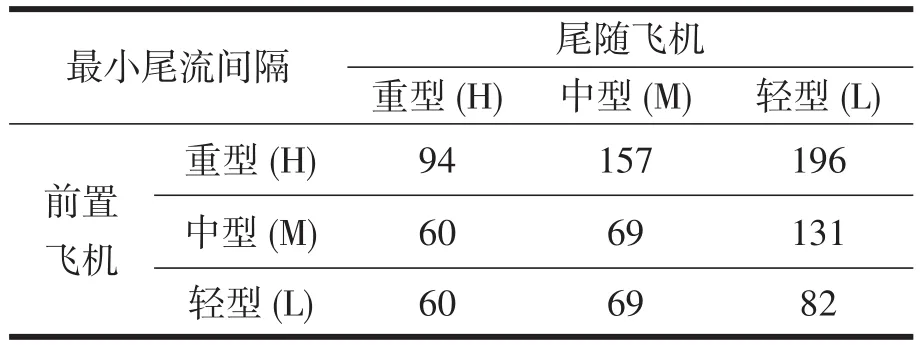
表1最小安全间隔（单位：秒）Table 1 Minimum safe separation(in seconds)

本约束旨在保证降落过程中任意两架航班之间的间隔需求，若航班i早于航班 j降落，则

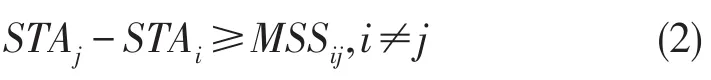
2.2.2 降落时间窗约束

受飞行性能和进场程序等条件限制，航班只能在特定降落时间窗内降落在跑道上，如式(3)，式中ETAi-TAmax为最早着陆时间，ETAi+TDmax为最晚着陆时间.此外，航班还可进行空中盘旋等待，因此降落时间窗扩展为若干个离散时间段，如式(4).

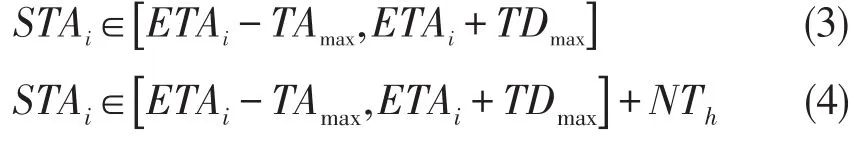
式中 N表示盘旋圈数；Th为航班在空中盘旋一周所需的平均时间.

2.2.3 CPS约束

考虑到管制员工作负荷和运行安全，Dear指出[6]，降落调度中过大的位置调整在管制运行中是不实际的，即调度前后航班位置的变动幅度不能超过一定的范围.例如最大位置偏移量为2，若某架航班在先到先服务的队列中排在第5位，则它在新队列中只能占据第3，4，5，6，7位.这不仅保证了一定的公平性，还可极大地缩小解空间.

设k为最大位置偏移量，航班i在初始队列中的位置为Ai，在新队列中的位置为A*i，则

2.2.4 进近航线约束

航班进港优化调度是通过调整航班序列来缩小延误的，即改变航班的前后位置，因而会发生航班超越的情况.而在实际运行中，由于终端区空域自由度低、冗余度小，除非必要，否则应尽可能避免大范围的调整，尤其是同航线航班后机超越前机情形，因为这不但会增加运行成本，而且也会增大管制员工作负荷，甚至降低运行安全.

为此，引入进近航线约束旨在航班优化调度过程中，为属于同一进近航线上的航班建立先到先服务法则，即航班位置交换只发生在所属不同进近航线之间的航班，在保证优化调度方案有效性的同时，提高调度方案的可操作性.式(6)表明同航线航班不得发生超越行为.用ARi表示航班i所处的进近航线，若ARi=ARj，则

3 求解算法

3.1 算法的基本原理

航班进港调度问题是一个多约束、高动态的非线性系统的组合优化问题，如何高效处理约束并快速求解是研究的难点[21].

遗传算法是目前解决大规模组合优化问题常采用的智能算法，该算法模拟自然遗传过程中的繁殖、杂交、突变等现象，通过选择、交叉、变异等作用机制优化种群，具有很强的全局搜索能力.传统遗传算法适合求解无约束优化问题，而对于约束优化问题，由于进化过程中会出现不可行解，因而必须采取新的方法来解决.

罚函数法[22-24]是求解约束优化问题常用的方法.罚函数的一般形式为

式中 Gi(x)和Hi(x)分别表示优化问题中个体违反第i个不等式约束和等式约束的程度，ri和si分别表示相应的惩罚因子.

通过调整惩罚因子平衡目标与约束，是罚函数方法处理约束优化问题的重要手段，但惩罚因子的选择往往比较困难.若惩罚因子选择过大，将导致优化曲面变得异常复杂，加之无法利用不可行解提供的有用信息，算法很容易陷入局部最优，很难找到全局最优解；若惩罚因子选择过小，则很可能收敛到不可行域.

鉴于此，本文提出基于协同进化的遗传算法.协同进化遗传算法包含航班进港调度问题决策解和惩罚因子两类种群.算法不仅考虑了两类种群内部个体之间的协作与竞争，还充分考虑了两类种群之间在进化过程中的协同影响与相互作用，如在进行个体评价时，需要利用其它种群的个体信息.CoGA算法通过两类种群的协同进化，自适应地调整惩罚因子，并得到航班进港调度问题的最优解.

航班进港调度问题的CoGA算法中包含两类种群，一类是用于进化决策解的种群X，此类种群包含M1个子种群Xj( j=1,2,…,M1)，子种群规模为M2，种群中的个体xi(i =1,2,…,M1×M2)表示航班调度问题的决策解；另一类种群是惩罚因子种群Y，其种 群规 模 为 M1，种 群 中 的 个 体yj( j=1,2,…,M1)用于表征Xj中个体所对应的惩罚因子.决策解子种群Xj中的每个个体利用对应的yj所表示的惩罚因子对该子种群的适应度函数进行计算，并进行遗传操作，进化t1代后获得新决策解子种群；根据决策解子种群Xj中所有解的优劣信息，对种群Y中个体yj，即惩罚因子的优劣进行评价；并对惩罚因子种群Y进行遗传操作，获得下一代惩罚因子种群.在每一代协同进化完成后，决策解子种群Xj采用新一代惩罚因子种群Y进行种群适应值计算，直到满足算法终止条件.最后通过比较所有历史最优解作为航班调度问题的解，同时，种群Y中所对应的最优个体即为最佳惩罚因子.

3.2 编码方法

遗传算法的编码方式是设计遗传算法的关键.航班进港调度问题约束数量巨大，求解困难，因此，对基于降落时间的编码方式进行改进，提出一种带约束处理的编码方式，有利于降低约束复杂度.

对于航班降落时间序列(S TA1,STA2,…,STAn)，其降落顺序表示为(s1,s2,…,sn)，是(1 ,2,…,n)的一个排列；相邻航班的降落时间差为(d1,d2,…,dn)，其中di=STAsi-STAsi-1.用C=(S ,D)表示染色体，即(s1,s2,…,sn,d1,d2,…,dn).由于需要满足最小安全间隔 di-MSSsisi-1≥0,(i =1,2,…,n)，则染色体可以重新表示为C=(S ,V )，即(s1,s2,…,sn,v1,v2,…,vn)，其中vi=di-MSSsisi-1，V=(v1,v2,…,vn).令

式(8)还可以进一步写成

通过这种带约束处理的编码策略，将安全间隔约束纳入编码过程，成功地降低了航班进港调度问题中的约束复杂度.

3.3 决策个体的适应度函数

式(7)罚函数中仅包含个体违反约束的程度，对于违反约束程度相等的两个个体，其违反约束的数量可能不同，实际上违反约束数量较少的个体可能离可行域更近一些.因此，罚函数同时是个体违反约束程度与违反约束数量的函数，其优化效果要更好[20].考虑到上述情况，决策种群中个体xi的适应度函数为越小，则P() yj越小，量.易知，

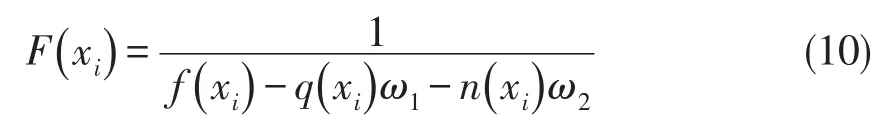
式中 f() xi表示航班调度优化问题的目标函数；q(xi)是个体xi违反约束的程度；n(xi)是个体违反约束的数量；ω1和ω2分别是Y种群中个体yj所对应的惩罚因子.

3.4 惩罚因子的适应度函数

（1）若Xj中包含至少一个可行解，则yj为有效个体，适应度函数为有利于算法向着违反约束程度较低和违反约束数量较少的方向进化.

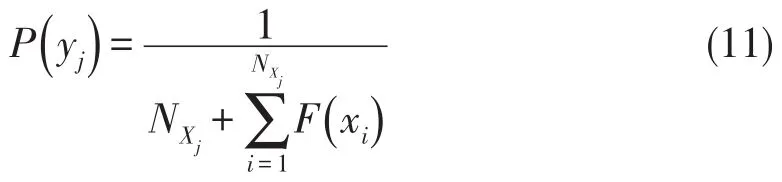
3.5 交叉变异

由于固定比率的交叉与变异操作易导致算法早熟，因此，本文应用一种自适应方法调节交叉率与变异率值.

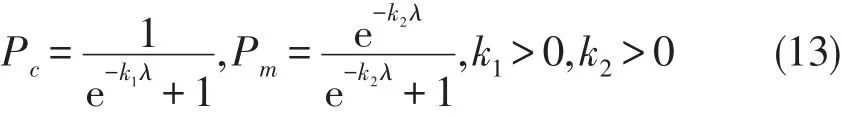
式中 λ=Fmax-F，用以表示早熟程度；Fmax表示种群中个体最大的适应值；F表示大于种群个体平均适应值的所有个体适应值的均值.

3.6 CoGA算法流程

航班进港调度问题中两类种群采用相同的遗传操作，具体算法流程如图1所示.

步骤1初始化决策解种群X，t1=0，初始化惩罚因子种群Y，t2=0；

步骤2X种群适应值评价；

步骤3Y种群适应值评价；

步骤4Y种群遗传操作；

步骤5到达Y种群极值则更新Y种群，转步骤6；否则t2=t2+ 1，转步骤3；

步骤6对各决策解子种群，分别以相应惩罚因子种群中的个体作为惩罚因子，并进行遗传操作，更新决策解种群；

式中 NXj表示Xj中所有可行解的总数，其适应值之和为.从式(11)可知，可行解数量越多或适应值之和越大，则P() yj越小，有利于算法向着可行解多且目标值好的区域进化.

（2）若Xj中无可行解，则yj为无效个体，适应度函数为

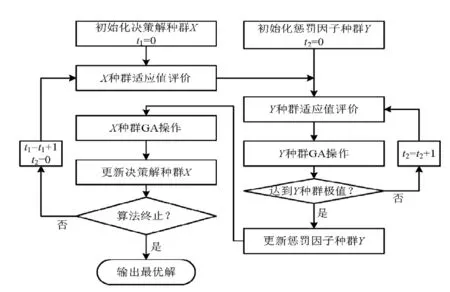
图1 CoGA算法流程Fig.1 The framework of CoGA algorithm

步骤7若满足算法终止条件，输出最优解；否则t1=t1+ 1，t2= 0转步骤2.

4 仿真实验与分析

为证明本文协同进化遗传算法的有效性，对北京首都国际机场某日某时段内25架航班进港数据进行仿真验证，并将本算法与标准遗传算法、先到先服务算法进行对比.CoGA算法的参数设置如下：惩罚因子种群规模M1=50，决策解子种群规模M2=100，决策种群迭代步数T1=100，惩罚因子种群迭代步数T2=100，种群初始交叉率Pc=0.8，初始变异率Pm=0.1.

表2给出了三种算法的调度结果，前五列分别为航班号、航班所属航线、机型、优先级和预计降落时间.后续几列给出分别使用先到先服务算法、标准遗传算法（k=2）、协同进化遗传算法（k=1,2,3）求解得到的降落顺序和优化降落时间.表3给出了三种算法的总额外代价与计算时间，从表中可知，优化算法结果明显优于先到先服务方法.

与先到先服务方法相比，GA算法的总额外代价降低了17.6%；CoGA算法在k=1,2,3时，总额外代价分别降低了16.7%、18.9%和20.4%.显然，当k值越大，优化效果越好.原因在于，当航班可交换位置的约束越宽松，算法则越有可能给出符合约束条件的更好的优化序列.

另一方面，随着k值的增大，计算时间也随之增加，GA算法在k=2时计算时间接近10 min，无法在短时间内得到优化解，很难应用于实际；CoGA算法在k=1,2,3时，计算时间分别为33 s、56 s和189 s，完全能够满足实时调度的需求.由于FCFS方法无优化过程，仅作为总额外代价优化效果的对比基准，因此其计算时间为0.

图2给出了GA算法与CoGA算法在k=2时的收敛性能.CoGA算法大约进化到20代左右时，适应度函数基本不变，算法收敛；而GA算法则需要大约50代左右才基本收敛.

表2 原始数据与算法仿真结果（单位：s）Table 2 Original data and simulation results(in seconds)

表3 三种算法的总额外代价与计算时间Table 3 Statistic results of FCFS,GA and CoGA algorithms

为分析不同规模下CoGA算法的有效性及效率，对航班数量规模分别为10、20、30、40架的数据进行仿真，每种规模下随机产生100个先到先服务航班队列，对这100个队列进行优化调度，并统计优化结果，取其平均值进行比较分析，如表4所示.

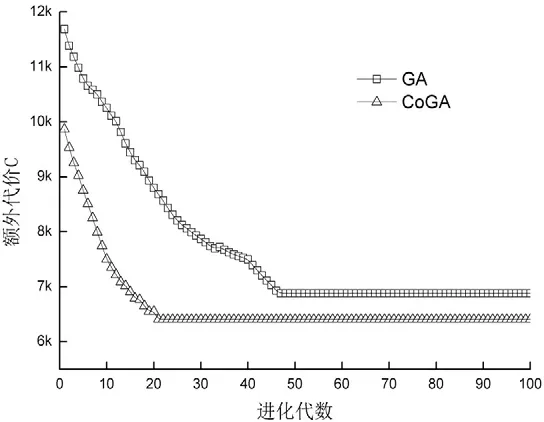
图2 总额外代价随进化代数的变化Fig.2 Total costs variations with evolution generation

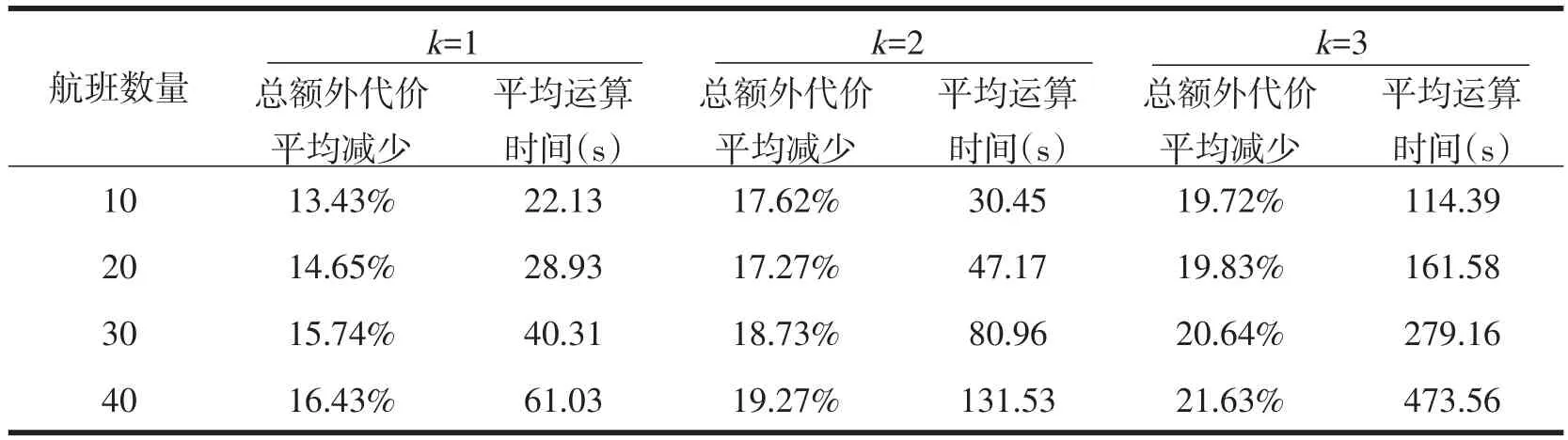
表4 不同规模下总额外代价最小优化结果Table 4 Optimal results of minimum total costs under various scales

由表4可知，CoGA算法优化效果随航班数量增加有小幅提升，这是由于当航班数量较少时，其相对于大量航班的可优化空间亦相对较小.虽然在不同的k值下运算时间有比较明显的差别，但即使是40架航班、k=2时平均用时也仅为131.53 s，远优于GA的10 min（25架航班，k=2）.

综上所述，对于多约束的航班进港调度问题，虽然GA算法全局搜索能力很强，但处理大量约束时依然存在很大局限，而本文设计的带约束处理的编码策略和协同进化算法可以有效处理问题中的大量约束，使得CoGA算法能够有效地解决航班进港调度问题，在优化效果与GA算法相当的情况下，有效降低计算时间，克服问题规模剧增导致的计算效率低下的难题.

5 研究结论

航班进港优化调度问题是空中交通管理系统关注和研究的热点问题，其实时性要求和多约束处理是优化求解的关键.本文构建了进港航班调度模型，并应用改进的协同进化遗传算法进行了求解.通过一种带约束处理的编码策略，降低了问题的约束复杂度，并通过种群间的竞争、协作改善算法性能.仿真结果表明，改进后的CoGA算法在航班进港优化调度上取得了较好的结果，同时运算时间较快，能够满足实际应用需要，为多约束、高动态的航班调度问题的求解提供了一条新的途径.

随着航空运输业的快速发展，空中交通流量、航班数量与跑道数量迅速增加，对运行效率的需求越来越高.应用CoGA算法对50架航班、4跑道、k=3规模下的调度问题进行求解时，由于解空间急剧膨胀，总额外代价的运算量大幅上升，虽然算法依然能够给出优化结果，但计算时间接近12 min，需要加入其它优化策略以进一步提升运算速度，这有待后续研究努力解决.

参考文献

[1]Andreussi A,Bianco L,Ricciardelli S.A simulation mod⁃el for aircraft sequencing in the near terminal area[J]. European Journal of Operational Research,1981,8(4): 345-354.

[2]Coumba D,Babacar M,Diaraf S.Scheduling aircraft landings at LSS airport[J].American Journal of Opera⁃tions Research,2012,2(2):235-241.

[3]Beasley J E,Krishnamoorthy M,Sharaiha Y M.Schedul⁃ing aircraft landings-the static case[J].Transportation Science.2000,34(2):180-197.

[4]Stiverson P,Rathinam S.Heuristics for a runway-queue management problem[J].Journal of Aerospace Engineer⁃ing,2011,225(5):481-499.

[5]Reza T,Mojtaba Y,Farzad R.Scheduling the sequence of aircraft landings for a single runway using a fuzzy pro⁃gramming approach[J].Journal of Air Transport Manage⁃ment,2012,25:15-18.

[6]Dear R G.The dynamic scheduling of aircraft in the near terminal area[R].M.I.T,Flight Transportation Laboratory Report,R76-9,1976.

[7]Balakrishnan H,Chandran B.Scheduling aircraft land⁃ings under constrained position shifting[C]//AIAA Guid⁃ance,Navigation,and Control Conference and Exhibit. Keystone,Colorado,USA,2006:21-24.

[8]LEE H,Balakrishnan H.Fuel cost delay and throughput tradeoffs in runway scheduling[C]//Proceedings of the American Control Conference.Seattle,USA,2008:2449-2454.

[9]朱星辉，朱金福，高强.基于约束编程的飞机排班问题研究[J].交通运输系统工程与信息,2011,11(6):151-156．[ZHU X H,ZHU J F,GAO Q.Aircraft scheduling based on constraint programming[J].Journal of Transpor⁃tation Systems Engineering and Information Technology, 2011,11(6):151-156.]

[10]Ciesielski V,Scerri P.An anytime algorithm for schedul⁃ing of aircraft landing times using genetic algorithms[J]. Australian Journal of Intelligent Information Processing Systems.1997,4(3):206-213.

[11]Cao Y,and Sun D.Greedy-heuristic-aided mixed-inte⁃ger linear programming approach for arrival scheduling [J].Journal of Aerospace Information Systems,2013,10 (7):323-336.

[12]Ciesielski V,Scerri P.Real time genetic scheduling of aircraft landing times[C]//Proceedings of the IEEE Con⁃ference on Evolutionary Computation.Anchorage,USA, 1998:360-364.

[13]Pinol H,Beasley J E.Scatter search and bionomic algo⁃rithms for the aircraft landing problem[J].European Journal of Operational Research.2006,171(2):439-462.

[14]Zhan Z H,Zhang J,Li Y.An efficient ant colony system based on receding horizon control for the aircraft arrival sequencing and scheduling problem[J].IEEE Transac⁃tions on Intelligent Transportation Systems.2010,11(2): 399-412.

[15]王世东，张越，张智海，等.繁忙机场航班降落排序的多目标优化[J].交通运输系统工程与信息,2012,12 (4):135-142.[WANG S D,ZHANG Y,ZHANG Z H,et al.Multi-objectives optimization on flights landing sequence at busy airport[J].Journal of Transportation Systems Engineering and Information Technology,2012, 12(4):135-142]

[16]Tian J,Xu H.Optimizing arrival flight delay scheduling based on simulated annealing algorithm[C].Physics Procedia,2012,33:348-353.

[17]冯兴杰，孟欣.基于免疫粒子群优化算法的航班着陆调度研究[J].计算机工程,2012,38(13):273-275,279.[FENG X J,MENG X.Research on flight landing schedule based onimmuneparticleswarmoptimizationalgorithm[J].Com⁃puterEngineering,2012,38(13):273-275,279.]

[18]孟祥伟，张平，李春锦.到场飞机排序及调度问题的Memetic算法[J].西南交通大学学报，2011，46(3):488-493.[MENG X W,ZHANG P,LI C J.Memetic algo⁃rithm for aircraft arrival sequencing and scheduling problem[J].Journal of Southwest Jiaotong University, 2011,46(3):488-493.]

[19]Dong B,Du W.Scheduling arrival aircrafts on multi-run⁃way based on an improved artificial Fish Swarm algo⁃rithm[C]//Proceedings of the 2010 International Confer⁃ence on Computationaland Information Sciences, Chengdu,Sichuan,China,2010:499-502.

[20]慕彩红.协同进化数值优化算法及其应用研究[D].西安:西安电子科技大学,2010.[MU C H.Co-evolution⁃ary numerical optimization algorithms and their applica⁃tions[D].Xi’an:Xidian University,2010]

[21]Zhang X,Zhang X J,Zhang J,et al.Optimization of se⁃quencing for aircraft arrival based on approach Routes [C]//Proceedings of the 10th International IEEE Confer⁃ence on Intelligent Transportation Systems.Seattle, USA,2007:592-596.

[22]Thomas P R,Xin Y.Stochastic ranking for constrained evolutionary optimization[J].IEEE Transactions on Evo⁃lutionary Computation.2000,4(3):284-294.

[23]Tessema B,Yen G G.A Self Adaptive penalty function based algorithm for constrained optimization[C].IEEE Congress on Evolutionary Computation.Vancouver,BC 2006:246-253.

[24]Liu J,Zhong W C,Jiao L C.An organizational evolution⁃ary algorithm for numerical optimization[J].IEEE Trans⁃actions on Systems,Man,and Cybernetics—Part B:Cy⁃bernetics,2007,37(4):1052-1064.

Optimal Scheduling of Aircraft Arrivals Based on Co-evolutionary Genetic Algorithm

ZHANG Xie，ZHAO Yi-fei，LIU Hong-zhi
（Tianjin Key Lab of Operation Programming and Safety Technology ofAir Traffic Management,CivilAviation University of China,Tianjin 300300,China）

Optimal scheduling of aircraft arrivals is a typical combinatorial optimization problem,which features complexity with multi-constraint.In order that the deficiencies can be overcome,which are multiconstraint,huge amount of computation and local optimum attraction,when the scheduling of aircraft arrivals is constituted with generic algorithms,a decision solutions population and a penalty factor population are constructed for the optimal scheduling problem,which is inspired by coevolution.The performance of the algorithm is improved by the competition and the coordination between the two populations.A coding strategy with constraints is designed,into which the safe separation constraint is coded,and the complexity of constraints is lowered with the coding strategy.Furthermore,an improved co-evolutionary genetic algorithm is proposed,and a simulation is conducted with the operational data from Beijing Capital International Airport. It is shown that the huge amount of constraints for the optimal scheduling can be tackled effectively with the approach proposed.When the optimal result corresponds to the result of original genetic algorithm,the time cost is reduced effectively and the difficulty is overcome,that the computation efficiency decreases sharply as the scale of the problem increases.

air transportation;co-evolutionary;genetic algorithm;aircraft arrival scheduling;air traffic flow management

1009-6744（2014）02-0094-08

V355.2

A

2013-08-29

2013-10-29录用日期：2013-11-18

国家自然科学基金（61039001）；国家科技支撑计划(2011BAH24B10)；中国民航大学科研基金(2011kyE04)；中国民航大学科研启动基金(2012QD04X).

张勰（1981-），男，陕西咸阳人，助理研究员，博士.*通讯作者：xiezhang@cauc.edu.cn