考虑风、潮联合概率分布的海堤超越频率分析

王灶平,刘桂平,龚 政,张长宽

(1.河海大学港口海岸与近海工程学院,江苏南京 210098;2.长江水利委员会水文局长江口水文水资源勘测局,上海 200136)

考虑风、潮联合概率分布的海堤超越频率分析

王灶平1,刘桂平2,龚 政1,张长宽1

(1.河海大学港口海岸与近海工程学院,江苏南京 210098;2.长江水利委员会水文局长江口水文水资源勘测局,上海 200136)

基于超越概率理论,选取最优Copula函数建立潮位和风速的联合分布函数,对江苏沿海条子泥匡围工程1989—2008年的实测年最高潮位和年最大风速资料进行分析,发现两者存在较弱的正相关关系;选取GH-Copula函数作为联合分布函数,计算得到风、潮组合的联合概率,进而求解其超越累积概率,发现风潮相关情况下的超越累积概率比风潮相互独立情况下高,认为工程中需考虑其联合概率。

海堤;潮位;风速;超越概率;联合概率分布;条子泥匡围工程

海堤是沿海地区重要的防潮防浪屏障,可有效地抵御风暴潮等海洋自然灾害,保障沿海地区人民的生命财产安全,是沿海地区经济和社会发展的生命线。海堤设防标准的关键在于设计潮位和设计波浪组合的合理性。在我国沿海地区,潮位和波浪的组合概率比较复杂,现阶段尚缺乏统一的表达形式。浙江、广东等南方大部分省市多采用风(浪)、潮同频率组合方式作为防御标准,而上海以北省市多采用重现期潮位与一定级别风速组合方式作为防御标准。哪种组合方式更为合理,目前尚无定论,国内学者为此做了大量研究。卢永金等[1-2]提出了基于重现期的超越概率理论,但是该理论基于潮位和波浪相互独立的假设,忽略了台风风暴潮的影响,该理论的完整性尚待进一步的论证。

本文以江苏沿海条子泥匡围工程为例,基于风、浪同频率的假设,在分析潮位和风速相关性的基础上引入基于GH-Copula函数的联合概率模型,进而求取两者的联合概率分布函数,探讨影响海堤设防标准的风、潮组合超越累积概率,以期完善超越概率理论,对基于风潮相关情况下的海堤超越累积概率进行理论分析和探讨。

1 条子泥匡围工程基本情况

条子泥位于江苏中部近岸浅海的辐射沙脊群中心区,为毗邻大陆岸滩的大型沙洲(图1)。条子泥匡围工程海域是东海前进潮波与南黄海旋转潮波两大潮波系统的交汇区,其水动力环境复杂,泥沙交换活跃,潮滩冲淤复杂多变。条子泥沙洲沿岸高滩属淤长型淤泥质海岸,潮滩宽阔、平缓,地形地貌复杂,近几十年来淤积趋势明显[3]。

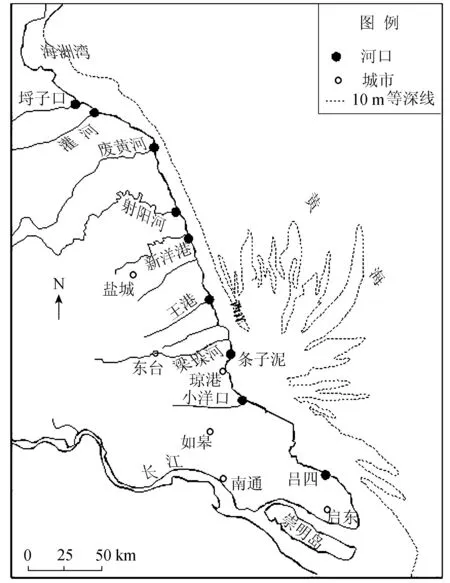
图1 南黄海辐射沙脊群及条子泥位置示意图

为缓解江苏沿海地区用地日益紧缺的矛盾、推动沿海经济发展,《江苏沿海滩涂围垦开发利用规划纲要》[3]中提出在2020年前匡围滩涂面积达到18万hm2,其中近期先期启动条子泥2.67万hm2沙洲匡围工程。工程布局见文献[4]。

2 潮位和风速的概率分布及两者相关性分析

2.1 设计潮位和设计风速

目前,江苏沿海只有北部的连云港站和南部的吕四站两个长期性的海洋观测站,两站距离条子泥匡围工程海域均较远,潮汐特性差异较大,难以直接采用其潮位资料。本文采用了条子泥匡围工程北侧梁垛河入海河口南闸闸下1989—2008年连续20年年最高潮位资料。采用Gumbel型曲线和Pearson-Ⅲ型概率分布曲线(以下简称P-Ⅲ型曲线)对年极值潮位序列进行拟合,如图2所示。由于潮位数据过于集中,若采用负偏的P-Ⅲ型曲线进行拟合,会使不同重现期的潮位值相差极小,于实际工程无意义。参考规范并综合考虑后,本文采用Gumbel型曲线拟合潮位。

由于缺少波浪年极值资料,基于风与风浪同频率的假设,使用风速资料代替波浪资料。根据临近条子泥地区的国际气象交换站东台站1989—2008年分方向的实测年最大风速资料,对向岸的E向风速进行频率分析,频率统计分布线型为P-Ⅲ型,由此得到不同重现期的设计风速。同时考虑到东台站距离海岸约50km,海上风速与海岸风速具有一定的差异,因此进行了陆-海岸-海上的风速订正[5]。参考《条子泥二期匡围工程可行性研究报告(送审稿)》[6]中的修正结果,取订正系数为1.96。经过修正后的风速资料,均值放大了1.96倍,其他统计参数不变。修正后的风速拟合见图3。

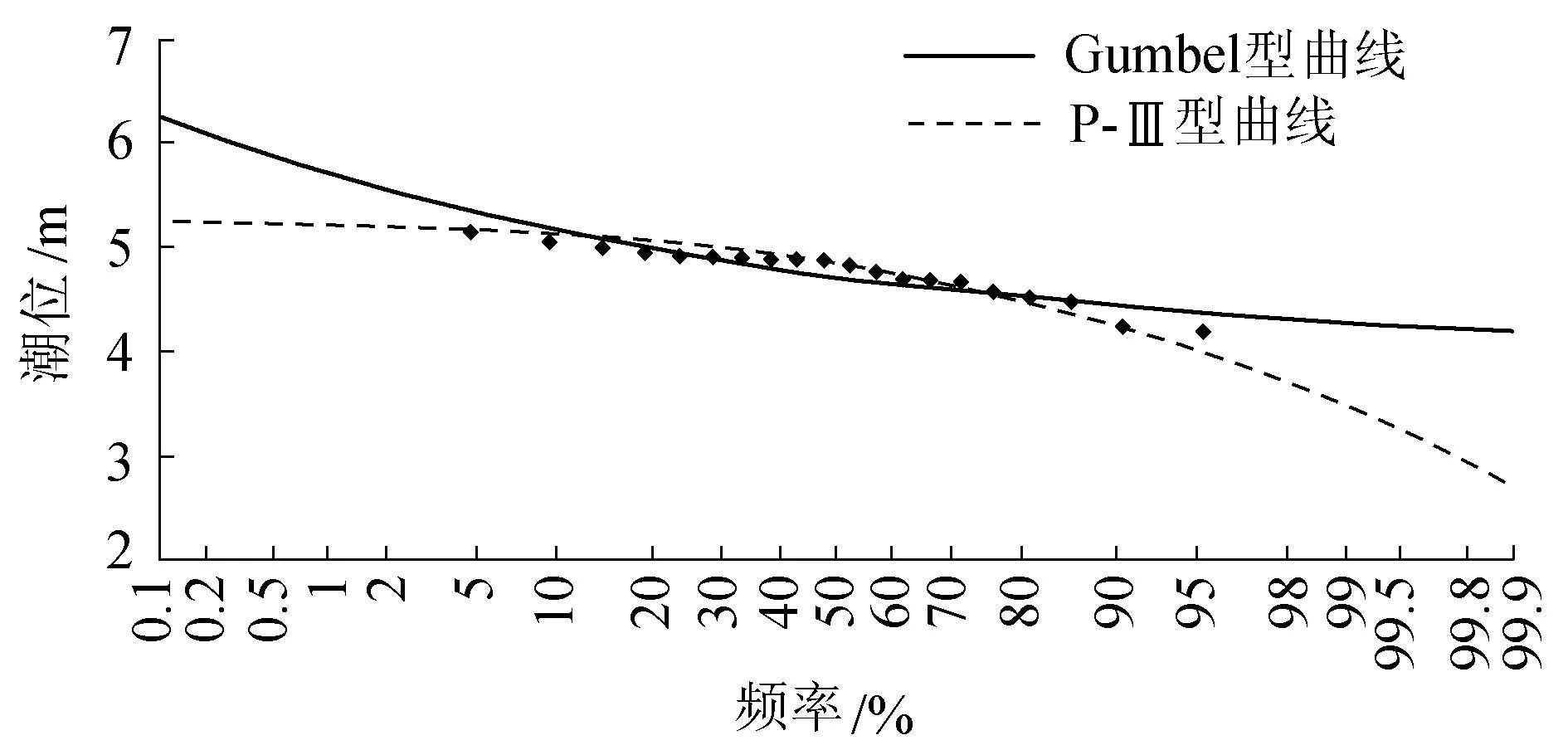
图2 年极值潮位拟合

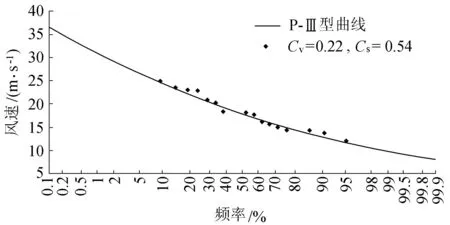
图3 年最大风速P-Ⅲ型曲线拟合结果

不同重现期潮位和重现期风速统计结果如下:重现期10a、20a、50a、100a对应的潮位分别为5.17m、5.34m、5.56m、5.72m,对应的风速分别为23.7m/s、25.55m/s、27.76m/s、29.30m/s。

2.2 相关性分析

研究2个变量的组合概率,首先需要考察其相关性,传统的方法是采用线性相关系数。该方法具有计算方便、线性变换不变性和度量多元正态分布相关性等优点,但在2个变量不服从正态分布时统计效果较差。Kendall相关系数法是表示多列变量相关程度的一种方法,一般采用等级评定来获得相关性系数。这种方法与常规的线性相关法相比,避开了变量的分布情况,对于随机变量的相关性检验较好。

Kendall相关系数可以由下式计算得到:

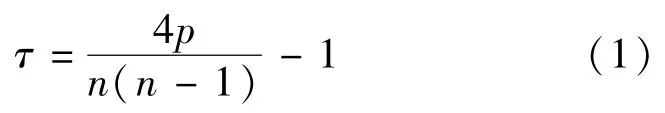
式中:n为样本容量;P为将所有的序列按照第一个分量排序后,第二个分量的排序能保持与第一个分量一致的大小顺序的数对个数之和。τ取值范围为[-1,1],τ从0至1增大时表示两序列正相关性增强,τ从0至-1减小时表示两序列负相关性增强。

选取条子泥地区梁垛河口南闸闸下1989—2008年年最高潮位和年最大风速作为2组样本,根据式(1)计算得到其Kendall相关系数为0.0587,可知年最高潮位和年最大风速之间存在较弱的正相关关系。

3 联合概率分布函数推求及检验

3.1 常用的联合概率模型

常用的联合概率分析模型包括Logistic模型[7]、Bilogistic模型[8]、Dirichlet模型[7-8]等。这些传统模型对变量分布有着严格的限制,不能适用于两变量任意分布的情况。本文中的随机变量分别服从Gumebel分布和Pearson-Ⅲ分布,没有固定的模型可以采用,在此引入Copula函数[9-14]。

作为相关性分析和多元统计分析的工具,Copula函数可以看成连接一元边缘分布和多元联合分布的函数。通过Copula方法,可以从边缘分布和Copula函数得出联合分布,从而大幅度简化联合分布的计算问题。Nelsen[15]曾系统地总结了Copula函数的性质和这个领域的主要研究成果。

根据Sklar定理,令F为具有单变量边缘分布函数F1,F2,…,Fn的n维分布函数,若边缘分布函数F1,F2,…,Fn连续,则存在一个唯一满足F(x1,x2,…,xn)=C(F1(x1),F2(x2),…,Fn(xn))关系的连接函数C。相反,如果C是一个n维Copula函数,那么F(x1,x2,…,xn)为n维分布函数。

根据Copula函数性质,构建两变量的联合概率分布模型可分2步进行:首先分别确定边缘分布FX(x)和FY(y),然后选择一个能够恰当反映变量间相关结构的Copula函数C(FX(x),FY(y))。令u=FX(x),v=FY(y),u、v为2组随机变量。几种常用的二维Copula函数如下:

式中θ为描述随机变量x、y相关关系的参数,与Kendall相关系数τ有关,可参考文献[16]中的公式估算。

3.2 联合概率模型优选

为了检验所采用的联合概率分布函数在风、潮联合概率分布中的拟合程度,一般将经验联合分布概率Femp和理论联合分布概率F进行比较。

二维联合分布的经验累积概率没有公认合适的计算公式可以利用,一般参照一维分布的经验累积频率计算方法,由下式[17]计算相应的经验累积概率:

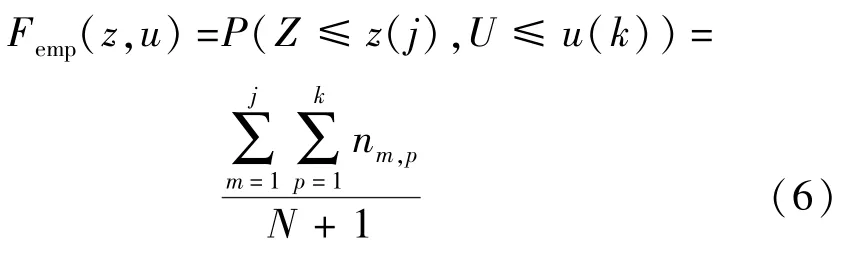
式中:Femp(z,u)为根据二元联合观测值(z,u)求出的经验联合分布,Z和U的联合观测值按升序排列后对应为(z(j),u(k));nm,p为联合观测值(z(m),u(p))发生的次数;N为联合观测值的个数。

图4为利用不同Copula函数计算得到的风潮组合经验联合累积概率和理论联合累积概率比较。根据图4可知,由联合概率分布理论函数确定的理论联合累积概率与相应的经验累积概率所确定的二维平面上的点均匀分布在45°直线的两侧,拟合效果比较好。

不同的Copula函数代表不同的相关结构,对Copula函数的选择将直接影响到一些分析和统计推断的结果[15],因此选择合适的Copula函数十分重要。择优选用Copula函数的主要检验方法有由图示直观选择Copula函数的Genest-Rivest方法[18]、离差平方和最小准则法[12]和AIC信息准则法[19]等。本文采用离差平方和最小准则法来择优选择Copula函数。离差平方和Sp的计算公式为

式中变量含义与式(6)中相同。

计算得到Clayton-Copula、AMH-Copula、GHCopula、Frank-Copula 4种Copula函数的Sp值分别为0.063 76、0.063 67、0.063 40、0.073 12。由此可知,根据离差平方和最小准则,GH-Copula函数拟合的Sp值最小,故选取该函数作为条子泥地区年极值潮位和风速的联合累积概率分布函数。

4 超越累积概率分析

对于海堤工程,设计潮位和设计风速的组合是分析确定海堤设防标准的依据。当潮位超过某一标准时,叠加一定风速下的风浪爬高,堤前水位会超过堤顶高程,出现一定概率的失事,即为超越累积概率。

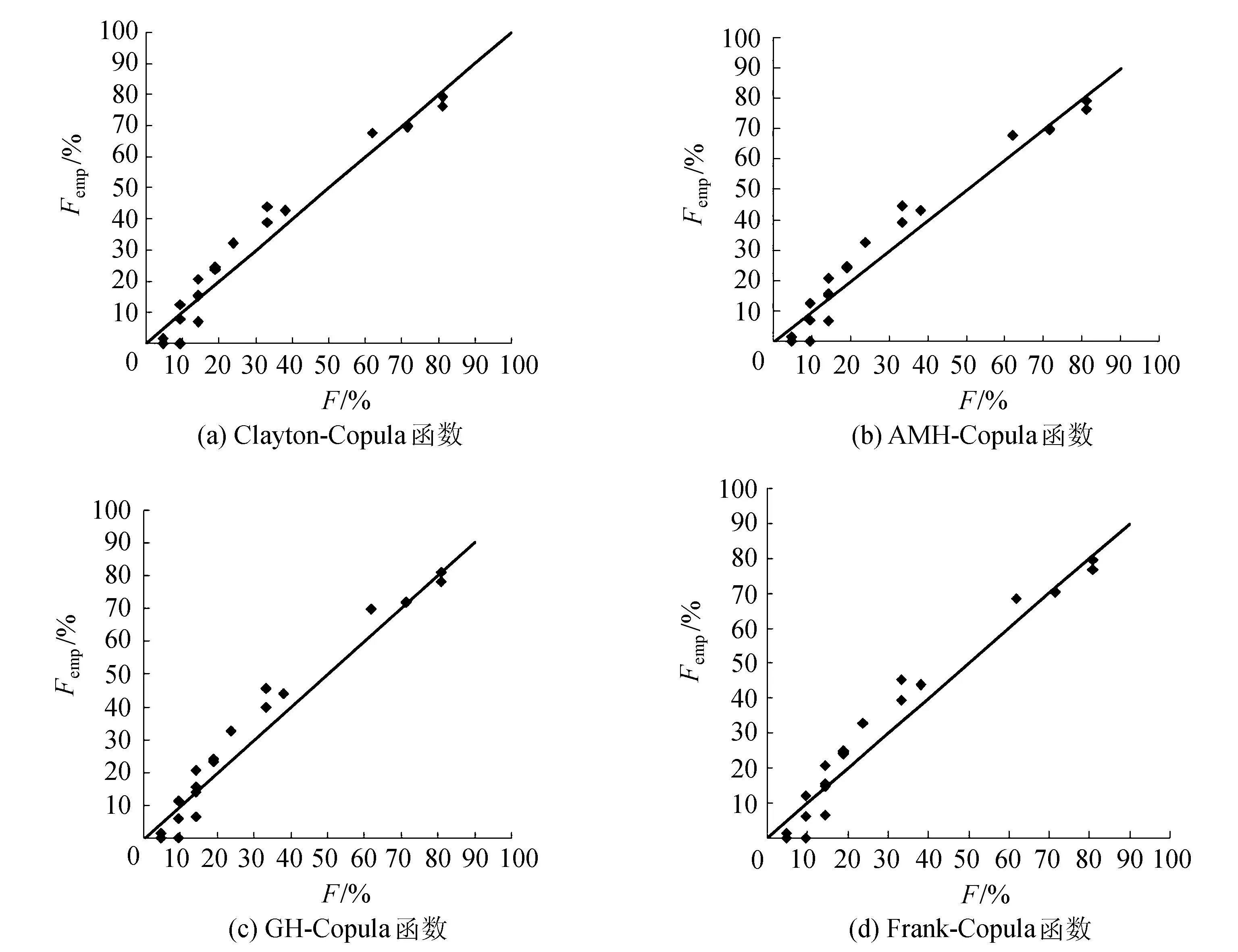
图4 理论联合累积概率与经验联合累积概率比较

潮位和风速联合超越累积概率通过下式求解:

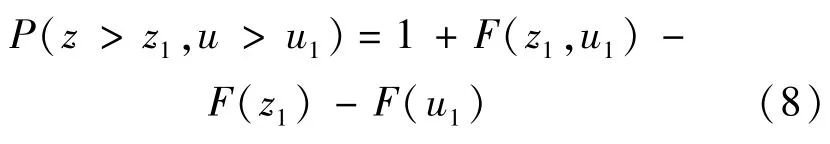
式中:F(z1,u1)为联合累积频率,F(z1,u1)=P(z＜z1,u＜u1);F(z1)、F(u1)分别为潮位和风速的累积频率。

对于不同频率的年极值潮位与风速的组合,由式(4)可以求得其联合分布概率,再由式(8)计算其超越累积概率,将频率换算成重现期,因此可以得到不同重现期的年极值潮位与年最大风速组合的超越累积概率。条子泥海堤超越累积概率计算成果见1。

表1 条子泥海堤超越累积概率

从表1可知,对于一定重现期的潮位,组合的风速越大其超越概率越小;对于一定重现期的风速,组合的潮位越大其超越概率越小。通过分析表1中对角线数据可以看出,高重现期风速叠加潮位和高重现期潮位叠加风速产生的超越概率是一样的,所以在制定海堤防御标准时应充分考虑风和风浪的影响。另外,由于潮位和风速具有一定的相关性,其超越概率大于两者完全独立情况下的概率。因此,在工程中需要考虑其联合概率。

对于如何在海堤设计中科学地选择设计潮位与设计风速进行组合,需要平衡超越概率与工程规模及投入资金之间的关系,力争做到风险小、投入少、安全系数高,在工程安全、资金投入之间寻求平衡点。

5 结语

以条子泥地区的年极值潮位和年最大风速资料为实例进行研究,基于Copula理论和方法构建年极值潮位和年最大风速的联合概率分布函数,对风潮弱相关情况下的海堤超越累积概率进行理论分析和探讨,许多方面尚不成熟,需进一步分析和证明。

在本文的分析过程中,为了简化计算,仅考虑了向岸风中的E向风,对于其他风向未进行讨论,今后需要进一步细化。

进一步的研究可参考国外可接受风险标准的制定方法,结合风险评价方法科学地确定年极值潮位和风速的组合标准问题,进而确定海堤设防标准。

[1]卢永金,何友声,刘桦.海堤设防标准探讨[J].中国工程科学,2005,7(12):17-23.(LU Yongjin,HE Yousheng,LIU Hua.Research on seawall flood defense criteria[J].Engineering Science,2005,7(12):17-23.(in Chinese))

[2]季永兴,张燎军,卢永金.基于超越概率的海堤防御标准理论探讨[J].水电能源科学,2011,29(1):37-39.(JI Yongxing,ZHANG,Liaojun,LU Yongjin.Theoretical discussion on defense standard of sea dike based on exceedance probability[J].Water Resources and Power,2011,29(1):37-39.(in Chinese))

[3]江苏省人民政府办公厅.江苏沿海滩涂围垦开发利用规划纲要[R].南京:江苏省沿海地区发展办公室,2010.

[4]龚政,张茜,赵亚昆,等.江苏沿海无资料地区海堤工程设计潮位推算方法[J].水利水电科技进展,2013,33(3):14-17.(GONG Zheng,ZHANG Qian,ZHAO Yakun,et al.A calculation method of designing tide levels for seawalls at Jiangsu coast without tide level observation data[J].Advances in Science and Technology of Water Resources,2013,33(3):14-17.(in Chinese))

[5]谢金赞.灌河口外水文动力条件分析[J].河海大学学报:自然科学版,1987,15(5):12-20.(XIE Jinzan.Hydrodynamic elementsin outer guanhe estuary[J].Journal of Hohai University:Natural Sciences,1987,15(5):12-20.(in Chinese))

[6]条子泥二期匡围工程可行性研究报告(送审稿)[R].南京:河海大学设计研究院有限公司,2012.

[7]谢华,黄介生.两变量水文频率分布模型研究述评[J].水科学进展,2008,19(3):443-452(XIE Hua,HUANG Jiesheng.A review of bivariate hydrological frequency distribution[J].Advances in Water Science,2008,19(3):443-452.(in Chinese))

[8]熊立华,郭生练.两变量极值分布在洪水频率分析中的应用研究[J].长江科学院院报,2004,21(2):35-37.(XIONG Lihua,GUO Shenglian.Application study of a bivariate extrernal distributionin flood frequency analysis[J].JournalofYangtzeRiverScientificResearch Institute,2004,21(2):35-37.(in Chinese))

[9]朱新玲.相关系数与Copula函数相关性比较研究[J].武汉科技大学学报:自然科学版,2009,32(6):664-668.(ZHU Xinling.A comparative study of Copula function correlationand correlation coefficient[J].Journal of Wuhan University of Science and Technology:Natural Science Edition,2009,32(6):664-668.(in Chinese))

[10]熊立华,郭生练,肖义,等.Copula联结函数在多变量水文频率分析中的应用[J].武汉大学学报:工学版,2005,38(6):16-19.(XIONG Lihua,GUO Shenglian,XIAO Yi,et al.Application of Copulas to multivariate hydrological frequency analysis[J].Engineering Journal of Wuhan University,2005,38(6):16-19.(in Chinese))

[11]肖义,郭生练,刘攀,等.基于Copula函数的设计洪水过程线方法[J].武汉大学学报:工学版,2007,40(4):13-17.(XIAO Yi,GUO Shenglian,LIU Pan,et al.Derivation of design flood hydrograph based on Copula function[J].Engineering Journal of Wuhan University,2007,40(4):13-17.(in Chinese))

[12]杨星,刘志龙,吴苏舒,等.海堤设计风浪和设计潮位组合风险率分析[J].上海交通大学学报,2012(10):1671-1674.(YANG Xing,LIU Zhilong,WU Sushu,et al.The risk probability analysis on design combination of wind wave and tidal level in design of sea dike[J].Journal of Shanghai Jiaotong University,2012(10):1671-1674.(in Chinese))

[13]刘曾美,陈子燊,李粤安.感潮河段洪潮遭遇组合风险研究[J].中山大学学报:自然科学版,2010,49(2):113-118.(LIU Zengmei,CHEN Zhishen,LI Yuean.Risk probability study on the combination of flood and tide for tide-affected river[J].ActaScientiarumNaturalium Universitatis Sunyatseni,2010,49(2):113-118.(in Chinese))

[14]尹志军,潘玉萍,沙文钰,等.风浪波高和周期的联合概率密度分布[J].海洋预报,2007,24(2):39-46.(YIN Zhijun,PAN Yuping,SHA Wenyu,etal.The joint probability density distribution of crest height and crest period[J].Marine Forecasts,2007,24(2):39-46.(in Chinese))

[15]NELSEN R B.An introduction to Copulas[M].New York:Springer Series in Statistics Springer,1999:216.

[16]MARSHALLAWO.Amultivariateexponential distribution[J].JournaloftheAmericanStatistical Association,1967,62:30-44.

[17]张娜,郭生练,肖义,等.基于联合分布的设计暴雨方法[J].水力发电,2008,34(1):18-21.(ZHANG Na,GUO Shenglian,XIAO Yi,et al.Design storm method based on bivariate joint distribution[J].Water Power,2008,34(1):18-21.(in Chinese))

[18]GENEST C R L.Statistical inference procedures for bivariatearchimedeanCopulas[J].Journalofthe American Statistical Association,1993,88:1034-1043.

[19]EMBRECHTS P,LINDSKOG F,McNEIL A.Modeling dependencewithCopulasandapplicationstorisk management handbook of heavy tailed distributions in Finance[M].New York:Elsevier Science Publishers,2003:329-384.

Exceeding cumulative probability analysis of seawall considering the joint probability distribution of tide level and wind speed

//WANG Zaoping1,LIU Guiping2,GONG Zheng1,ZHANG Changkuan1(1.College of Harbor,Coastal and Offshore Engineering,Nanjing 210098,China;2.The Survey Bureau of the Hydrology and Water Resources of Changjiang Estuary,Changjiang Water Resources Commission,Shanghai 200136,China)

Based on a present exceeding probability method,we selected an optimum Copula function to develop a joint probability distribution function of tide level and wind speed.The yearly maximum tide level and wind speed during 1989-2008 of Tiaozini Project in Jiangsu Province are adopted and we found a weak positive correlation between them.To calculate the joint probability,the GH-Copula function is selected as the joint distribution function.Considering the combination of tide level and wind speed,the exceeding cumulative probability is calculated.It is found that the exceeding cumulative probability is higher when the wind and tide are related than that in the case where the wind and tide are independent.Therefore,the joint probability should be considered in the project.

seawall;tide level;wind speed;exceeding probability;joint probability distribution;Tiaozini Project

P753

:A

:1006-7647(2014)06-0018-05

10.3880/j.issn.1006-7647.2014.06.004

2013-10-09 编辑:高建群)

国家自然科学基金(51379003);“十二五”国家科技支撑计划(2012BAB03B02);水利部公益性行业科研专项(201201045)

王灶平(1987—),男,江苏泰兴人,硕士研究生,主要从事海岸防灾减灾研究。E-mail:wangzaoping_hhu@163.com

龚政(1975—),男,江苏张家港人,教授,博士,主要从事河口海岸防灾减灾研究。E-mail:gongzheng@hhu.edu.cn