自密实轻骨料混凝土断裂全过程分析

吴 熙,范兴朗,吴智敏

(1.大连理工大学海岸及近海工程国家重点实验室,辽宁大连 116024;2.浙江工业大学建筑工程学院,浙江杭州 310014)

自密实轻骨料混凝土断裂全过程分析

吴 熙1,范兴朗2,吴智敏1

(1.大连理工大学海岸及近海工程国家重点实验室,辽宁大连 116024;2.浙江工业大学建筑工程学院,浙江杭州 310014)

为研究自密实轻骨料混凝土的断裂特性,引入以起裂断裂韧度为参数的裂缝扩展准则,采用数值方法分析了自密实轻骨料混凝土三点弯曲梁裂缝扩展的全过程,得到了不同缝高比的自密实轻骨料混凝土梁在三点荷载下的荷载-裂缝口张开位移曲线,并根据裂缝扩展准则,计算了自密实轻骨料混凝土的断裂过程区长度和裂缝扩展阻力曲线。结果表明:试验和计算的荷载-裂缝口张开位移曲线吻合良好,验证了裂缝扩展准则的正确性;试验断裂过程区长度随着裂缝增长先增大,达到完整断裂过程区长度后减小;自密实轻骨料混凝土的裂缝阻力随着裂缝长度增加而不断增大,初始缝高比对裂缝扩展阻力曲线数值和形状的影响并不明显。

自密实轻骨料混凝土;三点弯曲梁;断裂过程区;裂缝扩展阻力曲线

自密实轻骨料混凝土是在自密实混凝土和轻骨料混凝土的基础上发展起来的一种新型混凝土。自密实轻骨料混凝土可自密实成型,能减小施工难度,同时表观密度小,轻质高强,近年来已受到学者们的广泛关注。由于对自密实轻骨料混凝土有较高的工作性能要求,配合比和工作性能是当今研究自密实轻骨料混凝土的重点[1-4],而对于自密实轻骨料混凝土的断裂行为研究较少。

准确描述自密实轻骨料混凝土裂缝发展变化是提高自密实轻骨料混凝土断裂性能的基础。本文根据裂缝扩展准则,描述了自密实轻骨料混凝土的断裂全过程,得到了不同初始缝高比的自密实轻骨料三点弯曲梁的荷载裂缝口张开位移曲线,并将计算结果和试验结果进行比较,同时计算了三点弯曲梁在裂缝发展过程中断裂过程区长度以及基于黏聚力的裂缝扩展阻力曲线。

1 裂缝扩展准则

最早判断材料断裂的准则是在线弹性断裂力学基础上由Irwin提出的[5]。考虑到混凝土裂缝前端的断裂过程区引起的非线性,线弹性断裂力学的准则并不能直接运用于混凝土[6]。为了准确描述混凝土断裂过程,徐世烺等[7-11]引入起裂的概念,采用应力强度因子,提出了基于虚拟裂缝模型的裂缝扩展准则;其中,Dong等[8-10]认为,当外力引起的应力强度因子和黏聚力引起的应力强度因子的差值达到混凝土的起裂断裂韧度时,裂缝开始扩展,裂缝扩展准则可表示为

式中:K(P,a)为外力引起的应力强度因子;Kc(Δa)为黏聚力引起的应力强度因子;为起裂断裂韧度;P为作用于三点弯曲梁的外荷载;a为裂缝长度;Δa为裂缝扩展长度。

利用该准则,可以把裂缝发展的每一增量步Δa看作一个完整的断裂过程,均经历裂缝起裂和扩展两个阶段。这表明,在任意裂缝长度a时,裂缝是否扩展可如下判断:当K(P,a)-Kc(Δa)＜时,裂缝不扩展;当K(P,a)-Kc(Δa)=时,裂缝起裂;当K(P,a)-Kc(Δa)＞时,裂缝扩展。一旦裂缝扩展,裂缝长度增加为a+Δa,仍采用裂缝扩展准则判断裂缝是否满足下一步的扩展条件。据此,裂缝发展的全过程便能根据该准则进行描述。

该准则不仅可以用于Ⅰ型断裂,也可以推广至Ⅰ-Ⅱ复合型断裂[10]。现有的研究成果[8,10]表明,利用该准则可以准确地预测裂缝发展全过程,并计算任意裂缝长度a时的外荷载P,进而求解由外力引起的应力强度因子。

2 裂缝扩展过程分析

根据裂缝扩展准则,为了判断裂缝是否发展,必须求得K(P,a)、Kc(Δa)和。

对于给定裂缝长度a,如图1所示的三点弯曲梁的K(P,a)计算公式[12]为

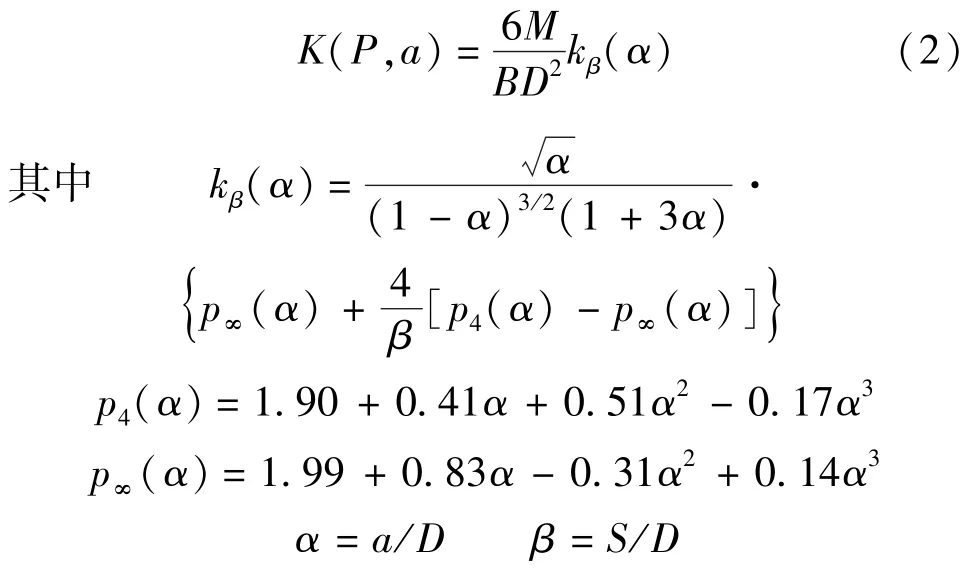
式中:M为外力P作用在试件上引起的弯矩;B为试件宽度;D为试件高度;S为试件跨度。

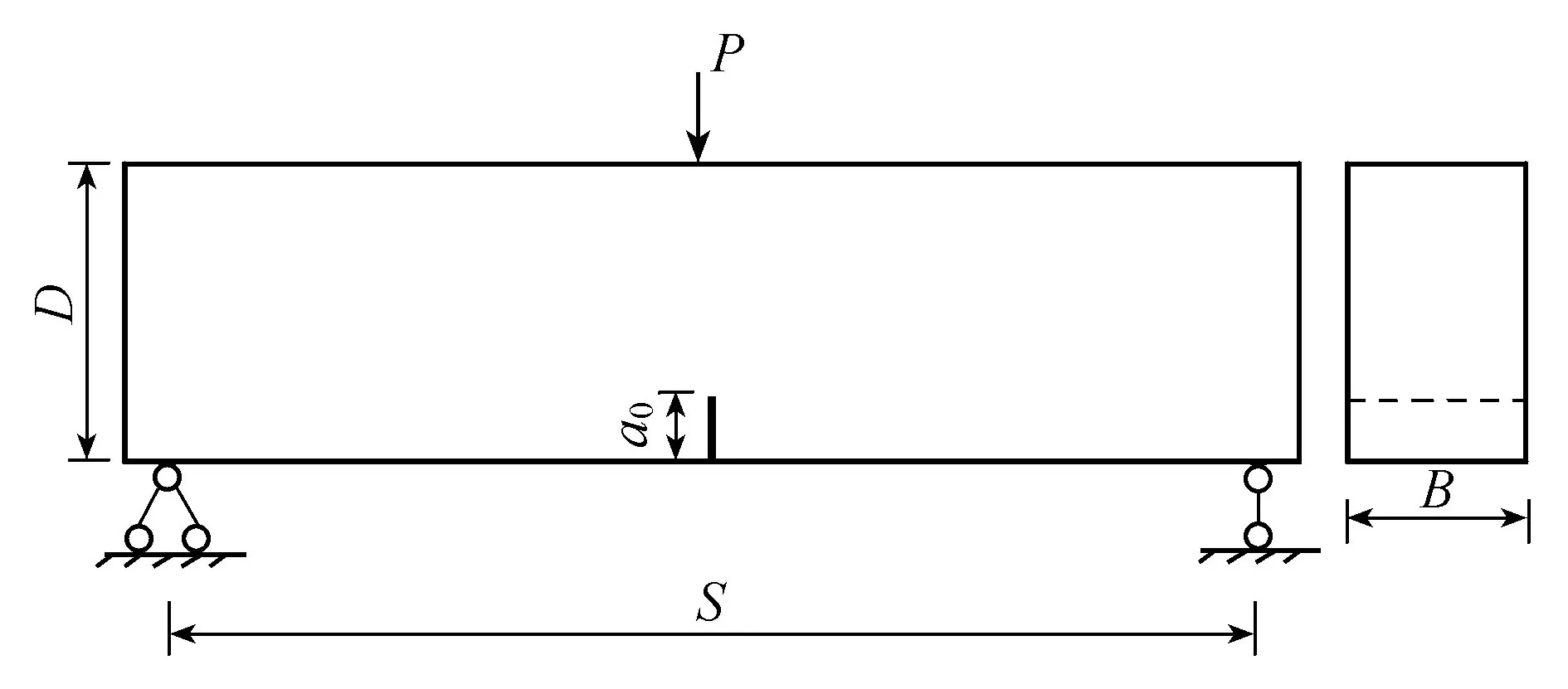
图1 三点弯曲梁

根据黏聚力模型,由黏聚力引起的应力强度因子[14]为

式中σ(x)为坐标x处的黏聚力。

目前,混凝土的软化曲线已出现多种形式,软化曲线的形状和相关参数的数值与混凝土断裂能GF有关[7,15]。针对轻骨料混凝土,本文采用Reinhardt等[16]提出的指数型软化曲线:

式中:ft为混凝土的抗拉强度;w为裂缝相对位移;w0为黏聚力为零时的裂缝相对位移,可根据断裂能GF确定;c1和c2为常数,对于轻骨料混凝土,c1=3,c2=5.64。

对于长度为a的裂缝,裂缝张开位移可由下式计算[17]:

式中V为裂缝口张开位移(crack mouth opening displacement,CMOD),其计算公式[12]为

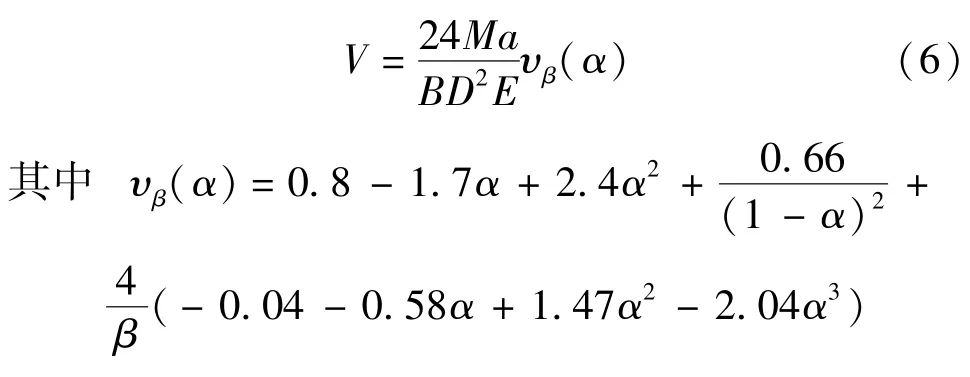
式中E为混凝土的弹性模量。

根据裂缝扩展准则,结合公式(1)～(6),可以计算三点弯曲梁在任意时刻的荷载P、断裂过程区长度、裂缝口张开位移V等参数。具体步骤如下:

a.输入试件尺寸参数(B、D、S等)和基本材料参数(ft、E、GF等)。

b.令P=Pini,a=a0,根据式(2)确定。

c.对于任意的裂缝长度a,假定荷载P,求解当前荷载下的K(P,a)和Kc(Δa),并判定是否满足裂缝扩展准则。若裂缝扩展准则不满足时,重新假定P,直至满足裂缝扩展准则。

d.计算当前裂缝长度a下的V和断裂过程区长度等。

e.持续增大裂缝长度至a+Δa,求解满足裂缝扩展准则的P、V等,直到试件破坏。

3 自密实轻骨料混凝土三点弯曲梁的断裂特性

采用三点弯曲梁研究自密实轻骨料混凝土的裂缝发展全过程。自密实轻骨料混凝土的配合比为1∶0.428∶1.965∶1.048∶0.471(水泥、粉煤灰、河砂、轻骨料、水质量比)。为了满足自密实混凝土的工作性能,添加了适当的高效复合减水剂,以增加混凝土的流动性。为了研究缝高比的影响,配制了4组不同缝高比的自密实轻骨料混凝土三点弯曲梁试件,尺寸均为100mm×100mm×500mm,净跨为460mm,跨高比为4.6,初始缝高比分别比为0.3、0.4、0.5、0.6。每组试件为3个,和GF均取3个试件的试验结果平均值作分析。三点弯曲梁的起裂断裂韧度和断裂能见表1,自密实轻骨料混凝土三点弯曲梁的试验详情可见文献[18]。

表1 自密实轻骨料混凝土的断裂参数

3.1 荷载裂缝口张开位移曲线

根据裂缝扩展准则计算的自密实轻骨料混凝土试件的荷载-裂缝口张开位移曲线和试验测得的3条荷载-裂缝口张开位移曲线见图2。从图2可见,试验值和计算值结果吻合良好,验证了裂缝扩展准则的正确性。可见,只需测得自密实轻骨料混凝土的基本材料参数,如抗拉强度、弹性模量和断裂能等,就可以根据裂缝扩展准则准确地描述自密实轻骨料混凝土裂缝发展的全过程。

3.2 断裂过程区长度变化

混凝土的断裂过程区长度为虚拟裂缝尖端至黏聚力为零处的长度。自密实轻骨料混凝土的三点弯曲梁的断裂过程区长度见图3。由于试件的初始缝高比不同,为了消除韧带长度对试验结果的影响,在图3中采用裂缝扩展长度和韧带长度的比值Δa/(D-a0)为横坐标。由图3可以看出,在达到完整断裂过程区长度之前,断裂过程区长度随着裂缝的扩展线性增大,当裂缝扩展长度达到0.7倍的韧带长度左右时,试件1～4的断裂过程区长度达到最大值,此时的断裂过程区长度为完整断裂过程区长度。完整断裂过程区长度的最大值和初始缝高比有关,初始缝高比越小,完整断裂过程区长度越大。不过,从图3可以看出,完整断裂过程区长度和韧带长度的比值约为0.7,基本不随初始缝高比变化。当断裂过程区长度达到完整断裂过程区长度之后,随着裂缝长度增加,断裂过程区长度逐渐减小,这是由于三点弯曲梁韧带较短,断裂过程区受到边界条件的约束,无法自由发展[19]。本文计算出的断裂过程区长度的变化趋势和文献[20-21]中观察到的断裂过程区长度变化相同。

图2 自密实轻骨料混凝土的荷载-裂缝口张开位移曲线

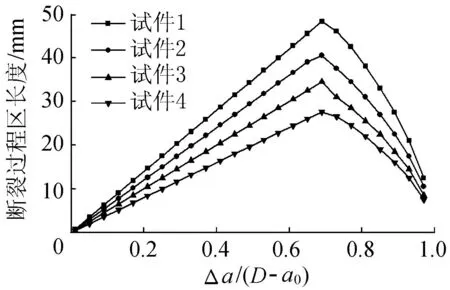
图3 自密实轻骨料混凝土的断裂过程区长度

3.3 自密实轻骨料混凝土的裂缝扩展阻力曲线

混凝土裂缝扩展阻力曲线可以判断裂缝的稳定发展状态,并可以应力强度因子的形式表达。一般混凝土的裂缝扩展阻力KR[22]可以表示为

根据裂缝扩展准则,求出Kc(Δa)和之后,可以根据式(13)求出自密实轻骨料混凝土的裂缝扩展阻力曲线。图4为4组自密实轻骨料混凝土试件的裂缝扩展阻力曲线,可以看出,裂缝扩展阻力随着裂缝长度增加单调上升。在裂缝发展前期,不同缝高比试件的裂缝扩展阻力曲线略有差异,但是该差异随着裂缝长度逐渐接近试件边界时逐渐减小。

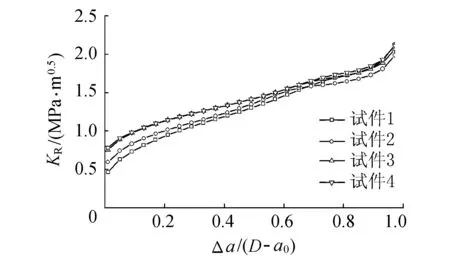
图4 裂缝扩展阻力曲线

4 结论

a.根据裂缝扩展准则,只需尺寸参数和基本的材料参数,就可以得到自密实轻骨料混凝土三点弯曲梁裂缝发展的全过程。根据裂缝扩展准则计算的荷载-裂缝口张开位移曲线和试验结果吻合良好,验证了裂缝扩展准则的正确性。

b.自密实轻骨料混凝土的三点弯曲梁的断裂过程区长度随着裂缝长度增长先增大,达到完整断裂过程区长度之后又随着裂缝长度增加而减小。完整断裂过程区长度约为韧带长度的0.7倍。

c.在本文的研究范围内,自密实轻骨料混凝土的裂缝扩展阻力随着裂缝增大逐渐增大,和初始缝高比的相关性不明显。

[1]SHI Caijun,WU Yanzhong.Mixture proportioning and propertiesofself-consolidatinglightweightconcrete containing glass powder[J].ACI Materials Journal,2005,102(5):355-363.

[2]CHOI Y W,KIM Y J,SHIN H C,et al.An experimental research on the fluidity and mechanical properties of highstrength lightweight self-compacting concrete[J].Cement and Concrete Research,2006,36(9):1595-1602.

[3]HWANG C,HUNG M.Durability design and performance of self-consolidating lightweight concrete[J].Construction and Building Materials,2005,19(8):619-626.

[4]WU Zhimin,ZHANG Yunguo,ZHENG Jianjun,et al.An experimental study on the workability of self-compacting lightweightconcrete[J].ConstructionandBuilding Materials,2009,23(5):2087-2092.

[5]ANDERSON T L.Fracture mechanics:fundamentals and applications[M].London:CRC Press,1995.

[6]WECHARATANA M,SHAH S P.Slow crack growth in cement composites[J].Journal of Structural Division,ASCE,1982,108(ST6):1400-1413.

[7]徐世烺.混凝土断裂力学[M].北京:科学出版社,2011.

[8]DONG Wei,WU Zhimin,ZHOU Xiangming.Calculating crack extension resistance of concrete based on a new crack propagation criterion[J].Construction and Building Materials,2013,38:879-889.

[9]吴智敏,董伟,许青.混凝土Ⅰ-Ⅱ复合型裂缝扩展准则及扩展全过程的数值模拟[J].水利学报,2009,40(2):180-187.(WU Zhimin,DONG Wei,XU Qing.PropagationcriterionformixedmodeⅠ-Ⅱcrack propagationandnumericalsimulationofthewhole propagationprocess[J].JournalofHydraulic Engineering,2009,40(2):180-187.(in Chinese))

[10]WU Zhimin,RONG Hua,ZHENG Jianjun,et al.A numerical method for mixed-modeⅠ-Ⅱcrack propagation in concrete[J].Journal of Engineering Mechanics,2013,139(11):1530-1538.

[11]邓爱民,徐道远.混凝土Ⅰ-Ⅱ复合型拉剪断裂试验研究[J].河海大学学报:自然科学版,2010,38(4):428-432.(DENG Aimin,XU Daoyuan.Tensile-shear fracture tests onⅠ-Ⅱmixed model of concrete[J].Journal of Hohai University:Natural Sciences,2010,38(4):428-432.(in Chinese))[12]GUINEA G V,PASTOR J Y,PLANAS J,et al.Stress intensity factor,compliance and CMOD for a general threepoint-bend beam[J].International Journal of Fracture,1998,89(2):103-116.

[13]XU Shilang,ZHU Yu.Experimental determination of fracture parameters for crack propagation in hardening cement paste and mortar[J].International Journal of Fracture,2009,157(1):33-43.

[14]JENQ Y S,SHAH S P.A fracture toughness criterion for concrete[J].Engineering Fracture Mechanics,1985,21(5):1055-1069.

[15]何敏,张东焕,王利民,等.混凝土断裂过程区拉伸软化的本构关系[J].水利水电科技进展,2010,30(4):8-12.(HE Min,ZHANG Donghuan,WANG Limin,et al.Constitutive relation for tension softening of concrete in fracture process zone[J].Advances in Science and Technology of Water Resources,2010,30(4):8-12.(in Chinese))

[16]REINHARDT H W,CORNELISSEN H A W,HORDIJK D A.Tensile tests and failure analysis of concrete[J].Journal of Structural Engineering,1986,112(11):2462-2477.

[17]JENQ Y S,SHAH S P.Two parameter fracture model for concrete[J].Journal of Engineering Mechanics,1985,111(10):1227-1241.

[18]吴熙,付腾飞,吴智敏.自密实轻骨料混凝土的双K断裂参数和断裂能试验研究[J].工程力学,2010,27(增刊2):249-254.(WU Xi,FU Tengfei,WU Zhimin.Experimental study on double-K fracture parameters and fracture energy of self-consolidating lightweight concrete[J].Engineering Mechanics,2010,27(Sup2):249-254.(in Chinese))

[19]MOREL S,LESPINE C,COUREAU J L,et al.Bilinear softening parameters and equivalent LEFM R-curve in quasibrittle failure[J].International Journal of Solids and Structures,2010,47(6):837-850.

[20]WITTMANNF,HUX.Fractureprocesszonein cementitiousmaterials[J].InternationalJournalof Fracture,1991,51(1):3-18.

[21]WU Zhimin,RONG Hua,ZHENG Jianjun,et al.An experimental investigationontheFPZpropertiesin concrete using digital image correlation technique[J].Engineering Fracture Mechanics,2011,78(17):2978-2990.

[22]XU S L,REINHARDT H W.Crack extension resistance and fracture properties of quasi-brittle softening materials like concrete based on the complete process of fracture[J].International Journal of Fracture,1998,92(1):71-99.

Analysis of crack propagation in self-compacting lightweight concrete

//WU Xi1,FAN Xinglang2,WU Zhimin1(1.State Key Laboratory of Coastal and Offshore Engineering,Dalian University of Technology,Dalian 116024,China;2.College of Civil Engineering and Architecture,Zhejiang University of Technology,Hangzhou 310014,China)

In order to study the fracture characteristics of self-compacting lightweight concrete(SCLC),the crack propagation criterion,which uses initial cracking toughness as the main parameter is used to numerically analyze the complete process of crack propagation in SCLC three-point bending beam.The criterion was verified by the reasonable agreement between calculated and experimental load-crack mouth opening displacement.According to the criterion,the length of fracture process zone(FPZ)and KR-curves of SCLC can be obtained.The results show that FPZ length increases with the crack extension and decreases after the full FPZ length.KRof SCLC specimens increases as the crack length increases and KR-curves of SCLC specimens,with different initial crack length ratio,shows insignificant differences in terms of shape and value.

self-compacting lightweight concrete;three-point bending beam;fracture process zone;KR-curves

TU528.2

:A

:1006-7647(2014)06-0036-04

10.3880/j.issn.1006-7647.2014.06.008

2013-08-15 编辑:熊水斌)

吴熙(1985—),女,四川泸州人,博士研究生,主要从事混凝土新型材料研究。E-mail:wuxi@zju.edu.cn