抗剪断参数对抗滑稳定可靠度指标的影响

李 斌,周兴波,孙 平

(1.西安理工大学水利水电学院,陕西西安 710048;2.中国水利水电科学研究院岩土工程研究所,北京 100044)

抗剪断参数对抗滑稳定可靠度指标的影响

李 斌1,2,周兴波1,2,孙 平2

(1.西安理工大学水利水电学院,陕西西安 710048;2.中国水利水电科学研究院岩土工程研究所,北京 100044)

为确定抗剪公式和抗剪断公式的适用工况,研究了岩体抗剪断参数不同均值、不同概率分布以及摩擦系数的变异系数对建筑物可靠度指标的影响;利用规范规定的岩体抗剪断参数对国内已建混凝土坝进行相应的可靠度指标计算和评价,并分别计算抗剪安全系数和抗剪断安全系数;按照规范规定黏聚力取对数正态分布,摩擦系数取正态分布,证明两者取值范围能够计算出合理的可靠度指标或安全系数,摩擦系数的变异系数对可靠度指标影响极大;建议岩体力学参数取值采用SL319—2005《混凝土重力坝设计规范》的规定值,黏聚力和摩擦系数的概率分布均选择对数正态分布为宜,抗剪公式和抗剪断公式适用于不同的工程地质条件。

抗剪强度;抗滑稳定;变异系数;概率分布;可靠度指标;重力坝;岩体

各种类型大坝的坝基和坝肩抗滑稳定是大坝整体稳定的关键,而在抗滑稳定计算过程中抗剪断参数的取值直接影响大坝的安全和效益[1],因而确定坝基和坝肩岩体抗剪断参数的离散特征至关重要。为掌握已建大坝工程岩体、结构面的抗剪断参数对安全系数和可靠度指标的影响程度,本文从风险分析[2]的角度对国内已建的11个具有典型意义的大坝进行抗滑稳定计算,研究抗剪断参数黏聚力c和摩擦系数f的不同取值、不同概率分布、不同变异系数对可靠度指标β的影响[3],并探讨按照抗剪断公式和抗剪公式计算β的不同。

1 可靠度分析方法

如图1所示的典型重力坝断面,假定其高度为h且上游面作用高度为H的水压力,计算时H=h,作用于坝基的扬压力呈三角形分布。则安全系数可由下式确定:

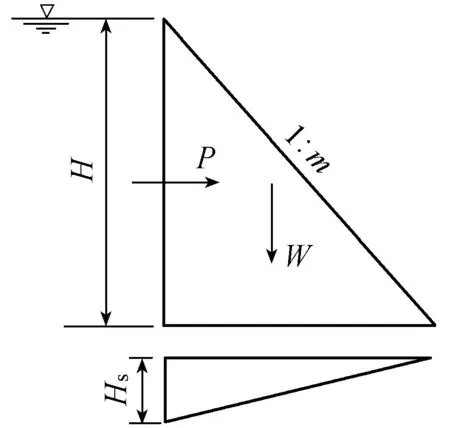
图1 典型重力坝断面示意图

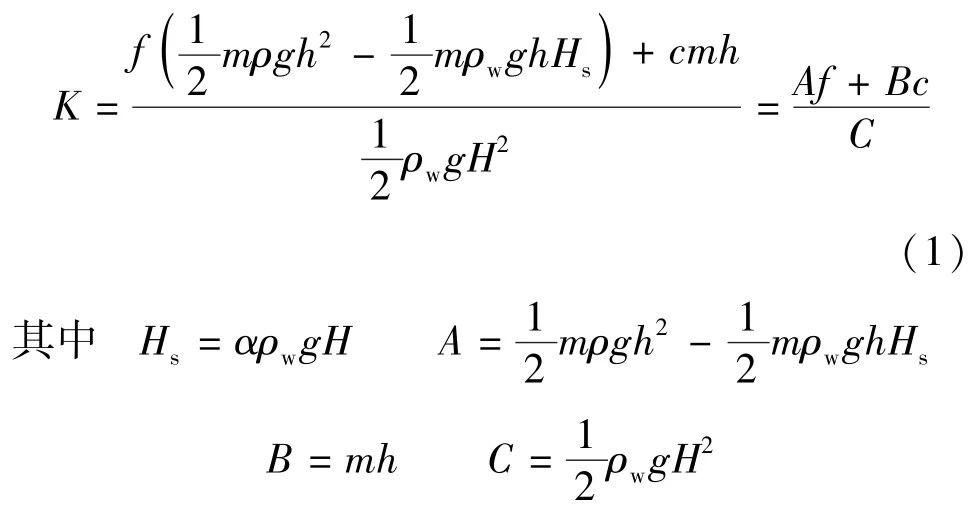
式中:ρ、ρw分别为坝体混凝土和水的密度;m为下游坝面坡度;.α为扬压力折减系数;Hs为扬压力;c、f分别为沿建基面的黏聚力和摩擦系数。

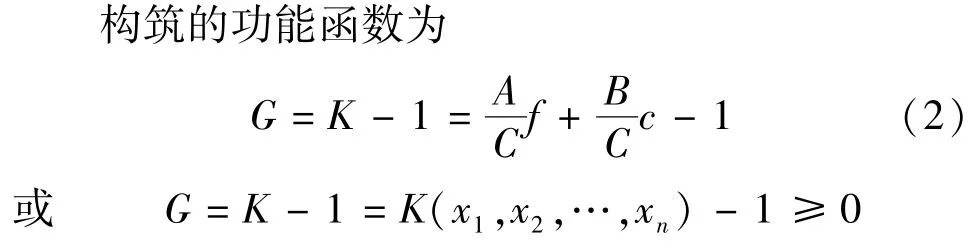
此时G为Ax1+Bx2+C的形式,令G的均值和标准差分别为μG和σG,则:

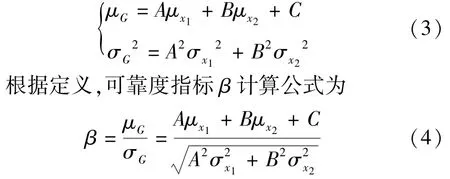
式(4)为计算重力坝深层抗滑稳定分析的可靠度指标计算公式。

2 抗剪断参数对可靠度指标的影响

2.1 参数均值对可靠度指标的影响

自20世纪90年代开始,我国水利水电设计规范在混凝土坝坝基岩体抗剪断强度的标准值、设计值方面相继出台了一系列的规定。鉴于水利、水电属于不同的行政主管行业,相应的规范在保持已有条文和框架下出现了不一致的地方,给设计分析工作带来诸多不便。如SL319—2005《混凝土重力坝设计规范》和DL5108—1999《混凝土重力坝设计规范》所建议的坝基岩体力学参数值都来源于GB50287—1999《水利水电工程地质勘察规范》,DL5108—1999认为GB50287—1999中表D.0.3和表D.0.5的数值为抗剪强度的实验均值,则标准值为将该数值进行0.2分位数折减后得到的相应值;而SL319—2005则认为表D.0.3和表D.0.5的数值为经过统计修正或考虑保证率、强度破坏准则等经验修正后确定的实验值,即为标准值。

应用水利和电力两套规范建议的岩体力学参数,对图1所示三角形重力坝按照沿建基面抗滑稳定进行可靠度分析,对于不同坝高下的抗剪断安全系数、材料分项系数折减后的可靠度指标进行了计算,结果见表1和表2。需要指出的是,表中f和c均值的计算是取m=0.7,α=0.3,ρ=2.3t/m3,ρw=1.0t/m3,按照f和c服从正态分布δ=μ-0.842V(δ为标准值、μ为均值、V为变异系数),取均值的0.8分位数为标准值进行计算得到。

从表1和表2可知,按照SL319—2005规定的建议值,Ⅰ类岩体相同的f和c取值条件下,150m坝高求得的β值比50m坝高求得的降低了33.6％～35.9％;150m坝高情况下,Ⅰ类岩体β值比Ⅱ类岩体大5.6％～12.3％。按照DL5108—1999规定的建议值,Ⅰ类岩体相同的f和c取值条件下,150m坝高求得的β值比50m坝高求得的降低了36.3％～40.2％;150m坝高情况下,Ⅰ类岩体β值比Ⅱ类岩体大7.9％～12.3％。

分别按照SL319—2005和DL5108—1999规定的建议值,在相同坝高、相同工况条件下,以Ⅰ类岩体50m坝为例,按SL 319—2005求出的β值比DL5108—1999大9.95％～12.95％。以Ⅱ类岩体50m坝为例,按SL319—2005求出的β值比按DL5108—1999求出的大11.2％～13.3％。以Ⅲ类岩体50m坝为例,按SL319—2005求出的β值比按DL5108—1999求出的大15.2％～21.2％。

表1 按SL319—2005建议的参数计算可靠度指标

按规范规定,在c和f分别为对数正态分布和正态分布的情况下,虽然根据SL 319—2005和DL 5108—1999建议的不同参数,在典型重力坝剖面条件下都取得了符合规范要求的安全系数和可靠度指标,但从表1和表2的计算结果看,DL5108—1999建议的坝基岩体力学参数过于保守,用分项系数方法求解安全系数时参数需要再经过两次折减,导致安全系数和可靠度指标计算结果偏低。建议坝基岩体力学参数取值采用SL319—2005的规定值,或者将DL5108—1999建议的坝基岩体力学参数均值看作标准值进行计算,这样既符合规范要求又避免了两个规范之间的不一致。

2.2 f和c不同概率分布函数对可靠度指标的影响

对三峡[4-5]、百色[6]、安康、大化、葛洲坝[7-9]、金安桥、武都[10-11]、岩滩、宝珠寺等工程在正常蓄水位工况下按抗剪断公式求出计算部位的安全系数k′和β值,结果见表3,并进行抗剪断强度下c和f不同概率分布函数对β值的影响分析。

表2 按DL5108—1999建议的参数计算可靠度指标

表3 9个工程的可靠度分析成果

在可靠度分析中,工程岩体与混凝土接触面c的变异系数取0.35,f的变异系数取0.2;结构面c的变异系数取0.40,f的变异系数取0.25。为研究方便,本文c和f的概率分布函数分别取正态分布和对数正态分布。

从表3可知:①当正常蓄水位工况下重力坝深层抗滑稳定的k′＞3.0时,其相应的β值都大于规范建议值4.2;②在c和f不同概率分布组合下β值基本存在β分布3＜β分布1＜β分布2＜β分布4的规律;安全系数或者可靠度指标计算时,f和c概率分布的选择应尊重试验结果;③根据不同概率分布条件下的安全系数和可靠度指标的关系,建议c和f的概率分布应选择对数正态分布为宜;④用抗剪断公式求安全系数及β值时,f概率分布一定的情况下,c概率分布取对数正态分布时对应的β值较大;而当c概率分布一定的情况下,f概率分布取正态分布时对应的β值较大。

2.3 f变异系数对可靠度指标的影响

针对官地和葛洲坝自然状态下的深层抗滑稳定问题,采用抗剪公式和抗剪断公式分别计算安全系数,按照抗剪强度和抗剪断强度选取的摩擦系数分别用f和f′表示,抗剪公式计算得到的安全系数用k表示,抗剪断公式计算得到的安全系数用k′表示[12]。考虑f变异系数Vf=0.1和Vf=0.2的情况并计算β值,对它们之间的关系进行研究。

2.3.1 官地水电站坝基深层抗滑稳定计算

雅砻江官地水电站工程枢纽挡水建筑物为混凝土重力坝,最大坝高168m。根据坝址区缓倾角错动带分布状况,溢流坝深层抗滑稳定属于以fxh01为第一滑面、坝趾下游岩体作为抗力体第二滑面的双滑面滑移模式。计算示意如图2所示,计算结果见表4。

2.3.2 葛洲坝水利枢纽坝基深层抗滑稳定计算

葛洲坝水利枢纽的泄水建筑物包括二江的27孔泄水闸、大江的9孔和三江的6孔冲沙闸3个部分。二江泄水闸的闸基为黏土质粉砂岩、砂岩互层,岩性软弱,基岩内有层面裂隙、软弱夹层等薄弱面;软弱夹层中有的已经泥化或局部泥化,其中以202号泥化夹层分布范围最广,软弱夹层的摩擦系数低至0.150～0.178,因此沿软弱夹层的深层滑动是二江泄水闸安全稳定的一个重要问题,坝体深层抗滑属于双滑面滑动,抗滑稳定和坝基扬压力示意如图3所示。将202号泥化夹层摩擦系数不同取值作为不同工况进行深层抗滑稳定计算,计算结果如表5所示。

表4 官地水电站深层抗滑稳定计算成果

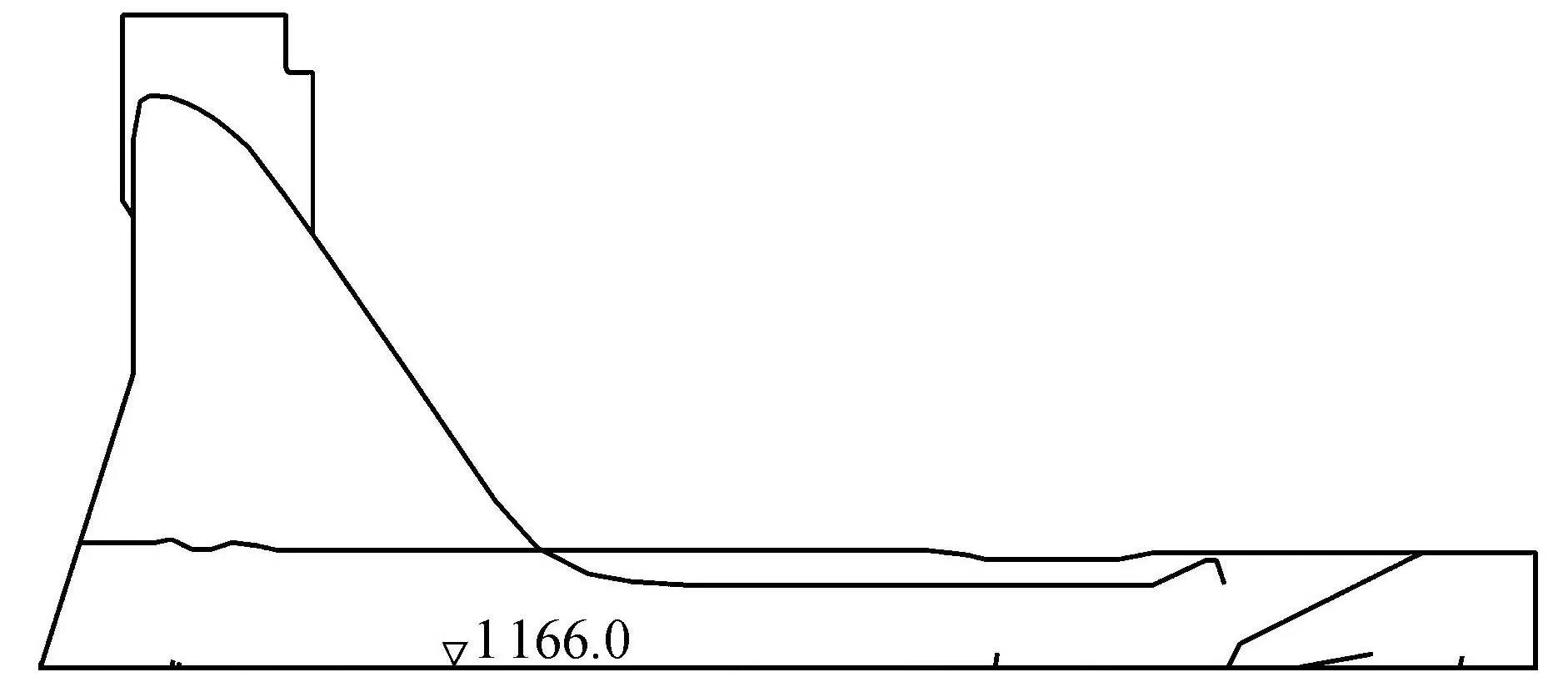
图2 官地重力坝抗滑稳定计算示意图(单位:m)

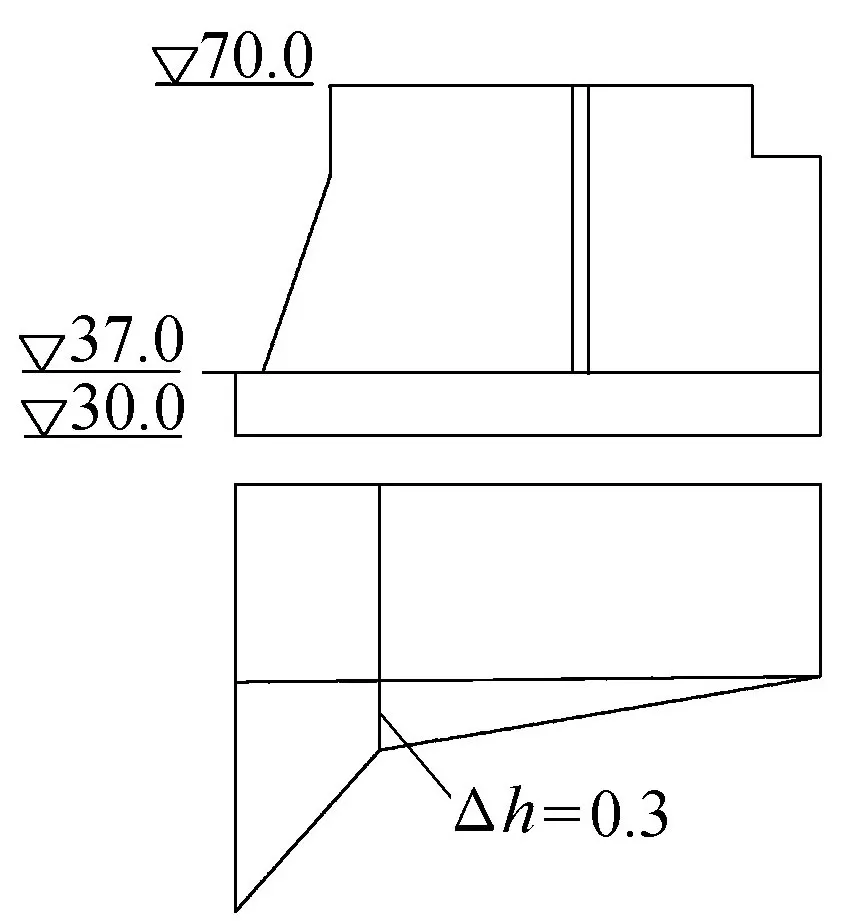
图3 葛洲坝水利枢纽坝基抗滑稳定和扬压力计算示意图(单位:m)

2.3.3 结果分析

对两工程实例的计算结果进行综合分析,结果如图4所示。

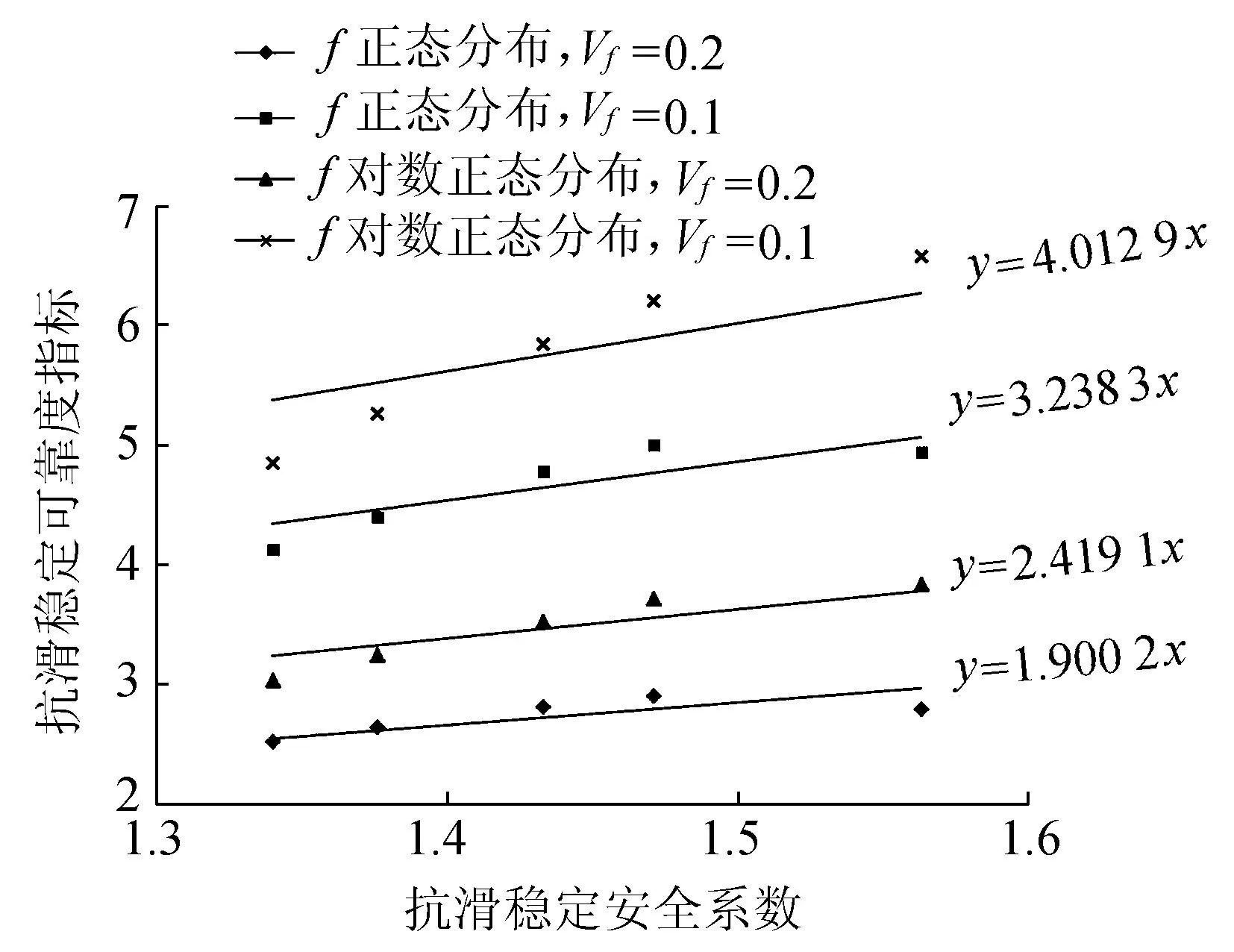
图4 不同f变异系数对可靠度指标的影响

从表4、表5和图4可以得到以下结果:①当f的概率分布取规范建议的正态分布且k＞1.3,对于Vf=0.1时β值都大于4.1;而对于Vf=0.2时β值在2.5～3.0之间。②用抗剪强度公式求β值,抗剪强度指标f取对数正态分布时,β值较大。基于抗剪强度指标计算的β值随安全系数的增大而增大;f的变异系数减小导致可靠度指标大幅增加,也从另一方面证明变异系数对β值影响较大;f为对数正态分布且Vf=0.1时,β值大于规范建议值4.2。③Vf=0.1时的β值大于Vf=0.2时的β值;相同变异系数情况下,f取对数正态分布时β值大于f取正态分布时的β值,以葛洲坝工程工况1为例,增大幅度约33％。④本文工程采用抗剪断公式与抗剪公式计算所得的安全系数如表4和表5所示。从表4和表5可以看出,当滑动面的c值较低时,2种公式计算得到的k′和k相差不大,如葛洲坝,k＞1,而k′远小于3.0。随着滑动面c值的增加,k′和k相差逐步加大,如官地,k′为3.0左右时,k为1.6左右。k′和k均满足规范规定的允许安全系数取值3.0和1.14。因此,当坝基存在软弱夹层时,对于不同的地质条件,应采用不同的计算公式。当滑动面c值较低时,采用抗剪公式较合适,当滑动面c值较高时,采用抗剪断公式较合适。

表5 葛洲坝抗滑稳定计算成果

3 结论

a.采用SL 319—2005《混凝土重力坝设计规范》和DL5108—1999《混凝土重力坝设计规范》所建议的坝基岩体力学参数,都能得到规范规定的安全系数,并在相同坝高、相同工况条件下,SL 319—2005比DL5108—1999所取计算参数大20％,计算得到的β值大10％～13％。

b.考虑随机变量和分布的再生性质、安全系数和可靠度指标的拟合程度,建议c和f的概率分布都选择对数正态分布为宜。

c.同一工程同一工况条件下,f变异系数取值对于可靠度指标的计算结果影响明显;变异系数减少50％,其可靠度指标增加60％。

e.对于抗剪断强度公式和抗剪强度公式算出的可靠度指标β值差异很大,建议坝基潜在滑移面由硬性结构面和岩桥组成时,按抗剪断公式进行抗滑稳定计算较合适;当坝基中存在着连续分布的软弱结构面(单滑面或双滑面均为软弱结构面),且结构面强度参数较低,采用抗剪断公式难以满足要求时,采用抗剪公式计算较合适。

[1]陈祖煜,汪小刚,杨健,等.岩质边坡稳定分析:原理·方法·程序[M].北京:中国水利水电出版社,2005:2016-2018.

[2]陈祖煜,陈立宏,孙平.非线性强度指标边坡稳定安全系数取值标准的研究[J].水力发电,2004,30(2):17-20.(CHENZuyu,CHENLihong,SUNPing.An investigation on the allowable factors of safety in slope stability analysis using nonlinear strength parameters[J].Hydropower,2004,30(2):17-20.(in Chinese))

[3]陈祖煜.土质边坡稳定分析:原理·方法·程序[M].北京:中国水利水电出版社,2003:273-306.

[4]戴会超,苏怀智.三峡大坝深层抗滑稳定研究[J].岩土力学,2006,27(4):643-647.(DAI Huichao,SU Huaizhi.Stability against sliding in intake dam section of Yangtze River Three Gorges Project[J].Rock and Soil Mechanics,2006,27(4):643-647.(in Chinese))

[5]葛修润,任建喜,李春光,等.三峡左厂3#坝段深层抗滑稳定三维有限元分析[J].岩土工程学报,2003,25(4):389-394.(GE Xiurun,REN Jianxi,LI Chunguang,et al.3D-FEM analysis of deep sliding stability of 3#dam foundation of left power house of the Three Gorges Project[J].Geotechnical Engineering,2003,25(4):389-394.(in Chinese))

[6]徐千军,李旭,陈祖煜.百色水利枢纽主坝坝基三维抗滑稳定分析[J].岩石力学与工程学报,2006,25(3):533-538.(XU Qianjun,LI Xu,CHEN Zuyu.Threedimesional stability analusis of dam foundation of baise hydro-junction[J].Chinese Journal of Rock Mechanics and Engineering,2006,25(3):533-538.(in Chinese))

[7]林伟平.葛洲坝基岩202号泥化夹层强度选取的探讨[J].水利学报,1982(10):68-72.(LIN Weiping.Gezhouba Dam bedrock 202 mud of interlayer strength selection[J].Journal of Water Resources,1982(10):68-72.(in Chinese))

[8]涂劲,周立本.重力坝深层抗滑稳定研究[J].水利学报,2003(10):96-100.(TU Jin,ZHOU Liben.Gravity dam stability against sliding[J].Hydraulic Engineering,2003(10):96-100.(in Chinese))

[9]田野.葛洲坝水利枢纽大江岩体力学性质报告[R].武汉:长江科学院,1981.

[10]唐成建,张全,潘杰.武都水库大坝河床坝基深层抗滑稳定分析[J].四川水利,2007,28(6):34-38.(TANG Chengjian,ZHANG Quan,PAN Jie.Analysis of stability against sliding for deep slide of bed dam base in Wudu Reservoir[J].Sichuan Water,2007,28(6):34-38.(in Chinese))

[11]彭明亮.武都水库坝址区岩体力学特性试验研究[J].四川水力发电,2003,22(2):45-46.(PENG Mingliang.Experiment study on rock mechanical property in damsite area at Wudu Reservoir[J].Sichuan Hydropower,2003,22(2):45-46.(in Chinese))

[12]苏怀智,刘红萍.高重力坝抗滑稳定安全度分析[J].水利水电科技进展,2011,31(4):20-23.(SU Huaizhi,LIU Hongping.Stability safety degree against sliding in high gravity dams[J].Advances in Science and Technology of Water Resources,2011,31(4):20-23.(in Chinese))

Influence of shear parameters on the reliability index of anti-sliding stability

//LI Bin1,2,ZHOU Xingbo1,2,SUN Ping2(1.Xi'an University of Technology,Department of Water Conservancy and Hydroelectric Power,Xi'an 710048,China;2.Department of Geotechnical Engineering,China Institute of Water Resources and Hydropower Research,Beijing 100044,China)

In order to determine the applicability of the shear formula and anti-cut formula,we present the studies of the impact of shear parameters of rock mass at different mean,probability distribution,and variation coefficient of friction coefficient f on buildings reliability index.Additionally,we calculate and evaluate the reliable indicator of domestic built concrete dam with shear parameters of rock works.In accordance with the specification,the coefficient c takes a lognormal distribution and the distribution f ranges of both institutions reasonably provide reliability index or safety factor,and the shear coefficient of variation of the parameter f has a great impact on the reliability index.The results show that the rock mass mechanics parameters should conform to specified value in the Design Specification for Concrete Gravity Dam(SL319-2005),and the probability distribution of c and f appropriately take a lognormal distribution model.Further,the shear formula and anti-cut formula are suitable for different operating conditions.

shear strength;anti-sliding stability;coefficient of variation;probability distribution;reliability index;concrete gravity dam;rock

TV642.3

:A

:1006-7647(2014)06-0031-05

10.3880/j.issn.1006-7647.2014.06.007

2013-11-13 编辑:胡新宇)

国家重点基础研究计划(973计划)(2013CB036403)

李斌(1984—),男(满族),河北承德人,博士研究生,主要从事水工结构研究。E-mail:lee_binbin@163.com