一种改进的局部多核学习算法

丁 跃

(重庆大学 数学与统计学院，重庆 401331)

0 引 言

支持向量机[1](Support Vector Machine)是建立在核函数基础上的机器学习算法,在模式识别、机器学习等领域有着广泛的应用.不同的核函数，同一核函数不同核参数,对于支持向量机泛化能力的影响是显著的[2],在一些复杂的问题中,特别是数据具有异构性,样本分布不平坦,单一核函数已经难以满足问题的需要,为此Lanckriet提出来多核学习算法。多核学习算法通过将这些核函数组合起来学习,得到更高的泛化能力。

关于多核学习算法的主要研究成果有Lanckriet等[3]首先使用了半正定规划技术,完成了对于核矩阵的学习问题，但是其在大规模数据和高维数据的学习上面，学习效率较低Sonnenburg 等[6]在多核函数锥组合的基础上,提出了一种通用而更有效的多核学习算法。 该方法将多核学习问题改写为一种半无限线性规划(Semi-infinite linear program, SILP) 形式, 新的规划形式可以在标准的SVM 应用问题中,利用成熟的线性规划方法进行求解. Rakotomamonjy等提出的简单多核学习 (SimpleMKL)[7]，引入新的混合范数将候选核函数的权系数包含在标准支持向量机的经验风险最小化中，目标函数转化为凸的、且光滑函数，在权系数的确定中，使用梯度下降算法，SimpleMKL，相比于其他算法获得更高的效率。

以上的多核学习算法对于所有输入样本，核函数的权系数是一样的，这无形中对样本进行了一种平均处理，局部多核学习算法(LMKL)利用选通函数，局部的选用了合适的核函数，但是，LMKL有以下的不足：LMKL算法所选用的选通函数有严重的参数参数沉余，其使用选通函数l1范数的形式，提高了核函数间的稀疏性，但是削弱了核函数间的“互补”作用。为此，本文提出了改进的局部多核学习算法(ILMKL),针对选通函数的参数沉余的问题，在其目标函数中加入正则项，并且使用选通函数的lp范数形式。

1 局部多核学习算法

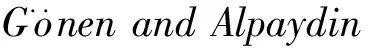
(1)

其核函数Km的权系数不再是常数，而是依赖于输入空间的样本数据，此时对应的判别函数为

(2)

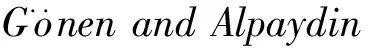
(3)

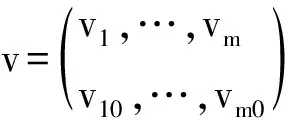
(4)

2 改进的局部多核学习算法(ILMKL)

在式(1)的合成核构造中，定义新的选通函数ηm(x)为

(5)

其中vm≥0为参数，这里选用的是选通函数的lp范数形式,有助于增强各个核函数间的“互补”作用,提高识别率。但是，不论是是式(3)还是式(5)中的选通函数都有参数“冗余”，可以看出，对于优化问题式(4),若v是上述问题的解，那么对于任意的常数v0,v+v0还是上述问题的解.所以它们都有参数“冗余”，为此，ILMKL算法在目标函数中加入了正则项||v||F,这里使用的是Frobenius范数.根据结构风险最小化原则。其学习问题可以表示为

(6)

为继承传统多核学习中不断迭代标准支持向量机代码的优势，将上述优化问题表示为

(7)

其中

这里参数u是用来平衡参数“冗余”和J(v)的值，对于固定参数v，将J(v)转化为其拉格朗日对偶形式：

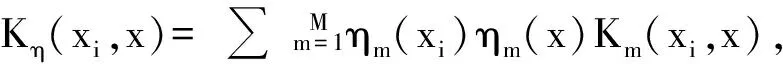
(9)

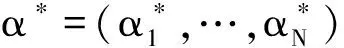
(10)

在给定参数v下，由于W(v)的解α*存在并且是唯一的[1]，于是W(v)对参数v的梯度向量存在，且等于如下形式：

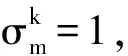
2.1 ILMKL算法描述

ILMKL算法以T(v)前后两次迭代的值小于设定的值ε或者迭代次数达到最大值为停机准则，算法具体描述如下：

1) 设选定候选核函数K1,K2,…,KM和参数u和p，参数v初始值v0，最大迭代次数G，迭代停止条件ε，迭代次数k=0；利用v0计算选通函数ηm(x)m=1,2，…，M，进而得到初始合成核K0；

2) 求解以Kk为核函数的标准支持向量机，计算目标函数值Tk(v)，梯度向量：

3) 线性搜索最优步长μk∈[0,+∞]；

4) 迭代vk+1=vk-μk*Dk(v)；

5) 计算Tk+1(v)，若|Tk+1(v)-Tk(v)|≤ε，或者k=G，则算法停止，否则，k=k+1，转到步骤2)。

2.2 ILMKL算法复杂度分析

ILMKL算法的的时间复杂度主要来源于以下几个方面：所使用标准支持向量机的复杂度，算法的迭代次数.本文使用的的是SMO算法[13]，其算法复杂度为在O(n1.2)与O(n2.2)之间，而其迭代次数受样本数据和迭代步长的选择的影响，假设迭代次数为k,所以算法的复杂度介于O(kn1.2)与O(kn2.2)之间。

3 实验分析

3.1 模拟数据实验

为验证ILMKL算法的有效性，本文模拟4个二元正态分布，从每个正态分布中产生100个数据，4个二元正态分布的均值分别为(-3,1)，(-1,-2.5)，(1,1)，(3,-2.5)，协方差矩阵分别为(0.8,0,0,2)，(0.8,0,0,4)，(0.8,0,0,2)，(0.8,0,0,4)，将第1和第3个二元正态分布作为一类，第1和第3个二元正态分布作为另一类.这里使用典型的传统多核学习算法SimpleMKL、局部多核学习算法LMSVM、和本文提出的ILMKL算法，分别对两类数据进行分类学习。选用3个线性核(KL-KL-KL),ILMKL算法选取参数u=(0,0.1,1),选取p=(1,2,3)，由于知道数据的真实分布，所以贝叶斯分类器是最优得分类器[14]。分别绘制了个算法的分类界面与贝叶斯分类器比较。

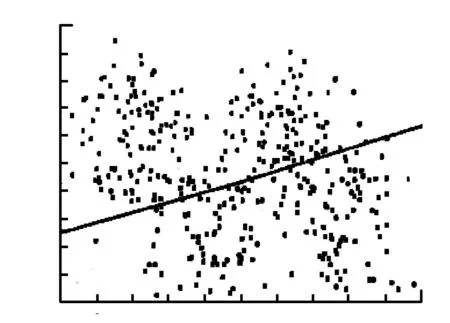
图1 简单多核学习

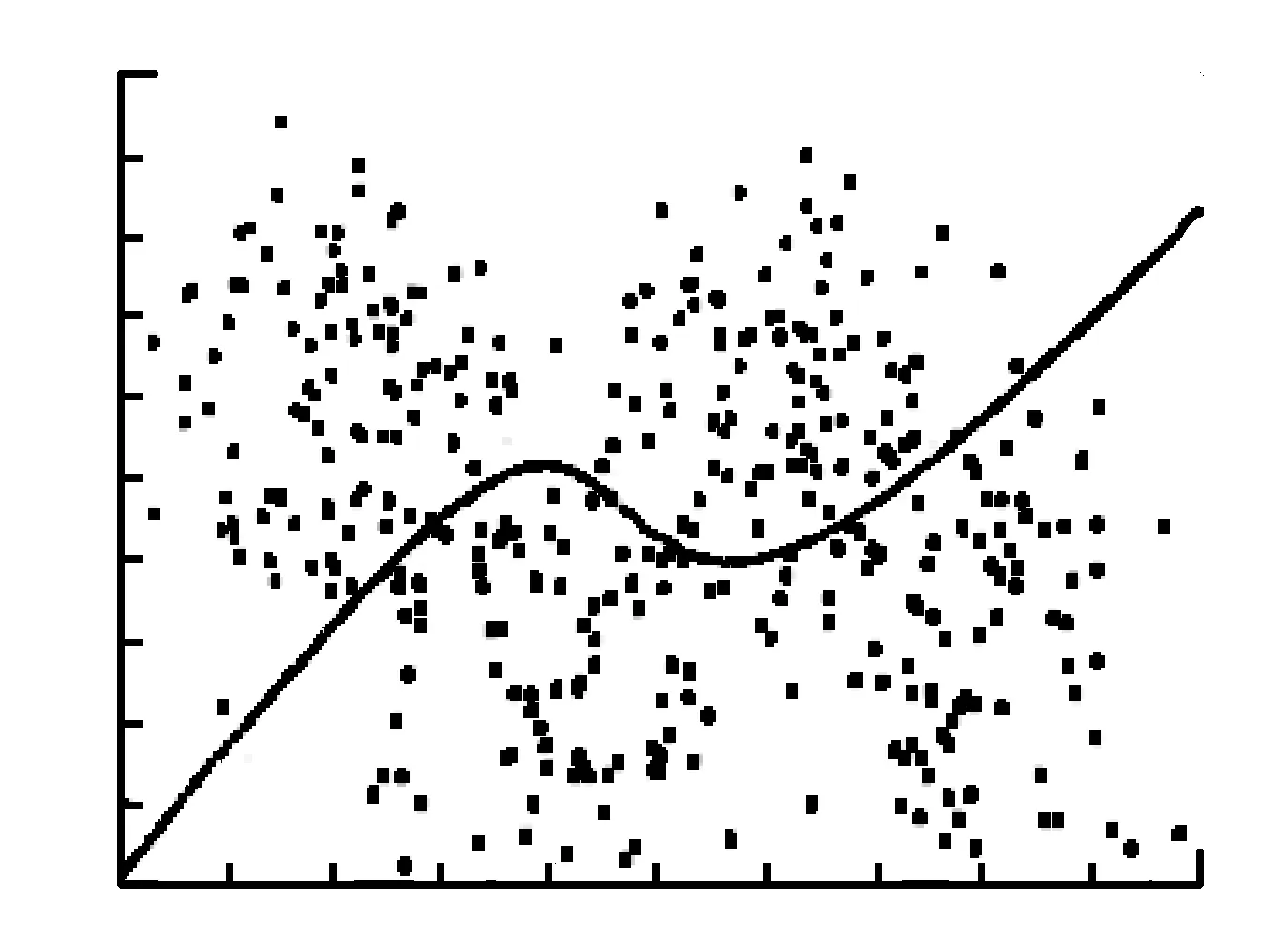
图2 局部多核学习

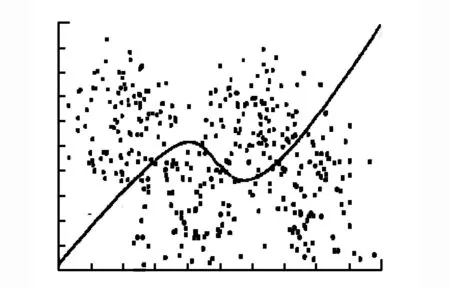
图3 改进的局部多核学习

图1、图2、图3中，虚线表示贝叶斯分别类界面，实线表示各个算法的分类界面，黑点表示支持向量。将图2和图3与图1比较，明显地显示了局部多核学习的优势。由于选用的核函数是3个线性核，传统多核学习算法SimpleMKL做出的类界面只是单纯的直线，局部多核学习可以通过选通函数局部的结合3个线性核，达到非线性分类的能力.比较图3和图2，ILMKL分类界面与虚线拟合的更好，从储存支持向量的个角度，ILMKL算法和LMKL算法的支持向量的个数最少。

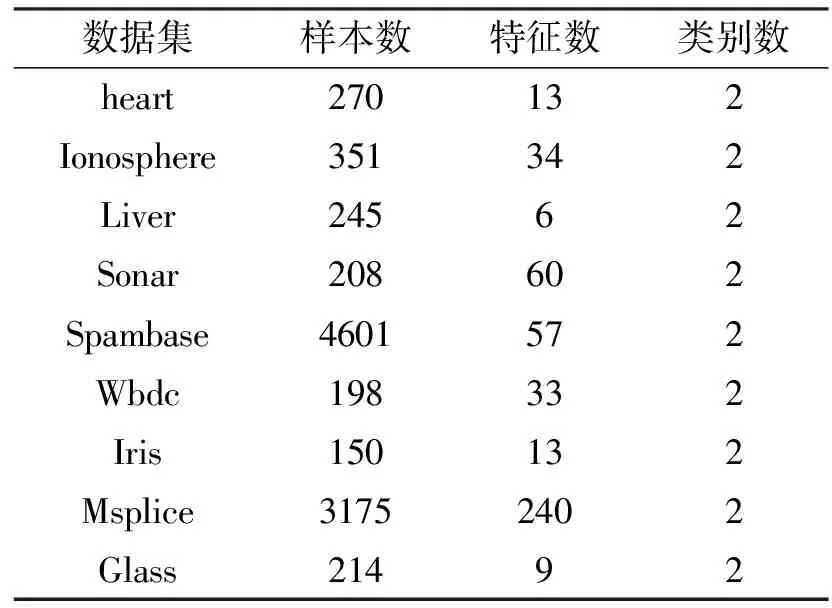
表1 实验所采用的数据集

3.2 UCI数据实验

将ILMKL算法、单核SVM[1]、LMKL算法[4]、SimpleMKL[7]算法应用到UCI数据库上，验证ILMKL算法的有效性，实验选取 9个UCI数据集，数据集的信息如表1所示。

实验所选用的核函数是线性核函数KL，二项式核函数Kp(x,x′)=(1+xTx′)2，高斯核函数KG,其中单核SVM分别使用上面的3个核函数计算，高斯核函数的参数σ采用以下方式估计：计算每一个样本与其他样本的最小欧式距离，将所有这些欧氏距离的平均作为核参数σ。采用交叉验证确定单核SVM、ILMKL、LMKL、SimpleMKL算法的惩罚系数C值，其中C∈{0.1,1,10}，选取ILMKL中参数μ∈{0.01,0.1,1,10},p∈{1,2,3,4,5,6,7,8}，表2记录了10重交叉验证的平均准确率，和多核支持向量机存储的平均支持向量数，所有实验结果，都是重复10次的平均结果。

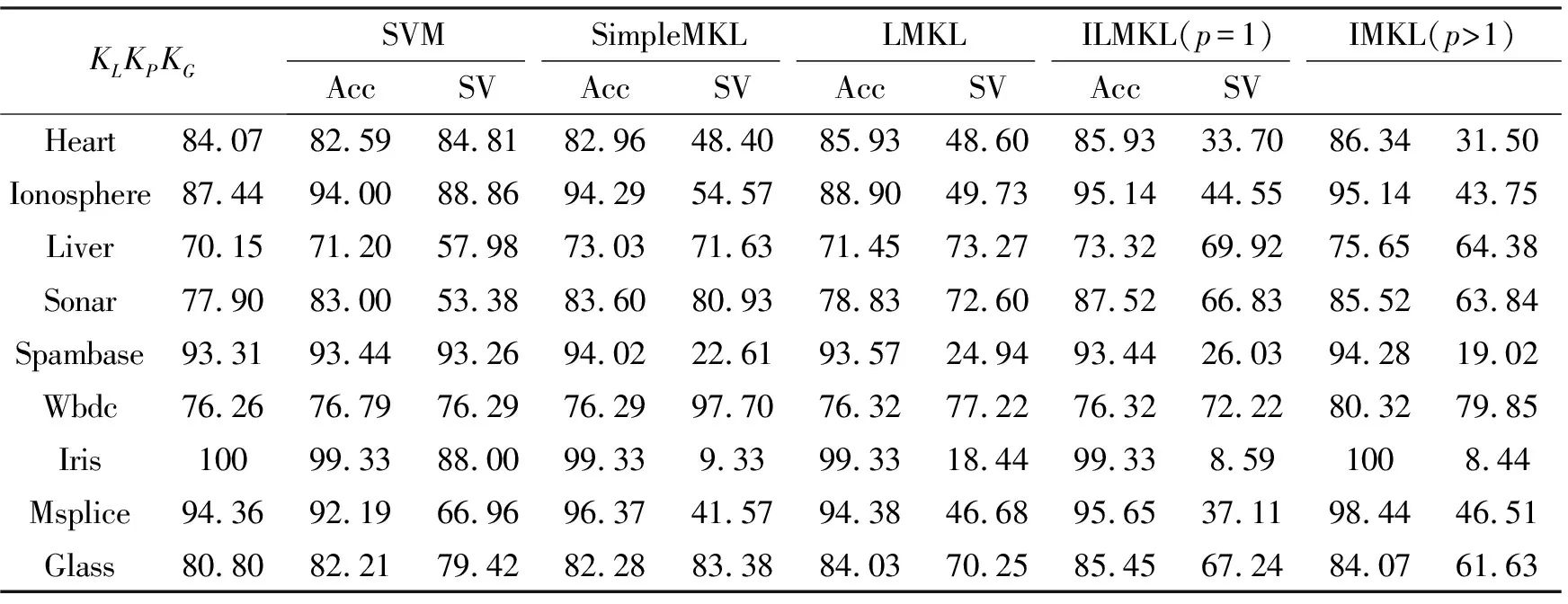
表2 实验结果

从分类精度的角度，LMKL，SimpleMKL算法基本相同，ILMKL算法分类精度最高，其中ILMKL(p>1)要比ILMKL(p=1)分类精度更高，这是因为核函数间不同的核映射有“互补”的作用，而使用1范数(p=1)会提高核函数间的稀疏性，这样会消弱核函数间的“互补”作用，进而影响分类精度。与单核SVM比较，ILMKL算法在这些数据集上都高于精度最高的单核SVM，SimpleMKL算法在除Heart，Iris数据集以外，其他数据集上都要高于精度最高的单核SVM，LMKL算法在除Iris Ionosphere数据集以外，其他数据集上都要高于精度最高的单核SVM，这点也表明多核学习算法有更好的分类精度。从存储的支持向量上来看，ILMKL算法存储的支持向量最少。

4 结 论

本文提出改进的局部多核学习算法，针对LMKL算法中选通函数的参数沉余的问题，在其目标函数中加入正则项，并且使用选通函数的p范数形式。对比实验结果表明：ILMKL有更高的泛化能力和存储更少的支持向量.未来的工作，将进一步提升该算法的泛化才能和效率，并将考虑将该方法推广到多分类或回归等其他领域。

参考文献：

[1] VAPNIK V. The Nature of Statistical Learning Theory[M]. NewYork：Springer-Verlag, 1995

[2] LANCKRIET C, VAPNIK V,BOUSQUET O, Choosing multipleparameters for supp-ort vector machines[J]. Machine Learning, 2002,46(1): 131-159

[3] LANCKRIET G, CRISTIANINI N, BARTKETT P, GHAOUI L,JORDAN M. Learning the kern-el matrix with semi-definite programming[J].Machine LearningResearch,2004,5(1): 27-72

[5] BACH F, Lanckriet G G, Jordan M I. Multiple kernel learning, conic duality, andthe SMO algorithm[C]. In: Proceedings of the 21st International Conference on Machine Learning Ban, Canada: ACM, 2004. 41-48

[6] SONNENBURG S, RATSCH G, SCHAFER C. A general and efficient multiple kernel learning algorithm[J]. Advances in Neural Information Processing Systems. 2006,18(1):1 273-1 280

[7] RAKOTOMAMONJY A, BACH F, CANU S, GRANDVALET Y.Simple MKL[J].Machine Learnin-g Research, 2008, 9(11): 2491-2521

[8] 汪洪桥,孙富春. 多核学习方法[J]. 自动化学报,2010,26(8):1037-1050