W/O乳化液油水分离数值模拟研究

田 敏， 颜 欢

(重庆工商大学 废油资源化技术与装备教育部工程研究中心，重庆 400067)

无论是原油还是成品油，在贮存和使用的过程中都会不可避免的受到外界环境的污染，如大气液滴掺杂到油液中。水分会促使油品降解和酸性物质的形成，造成油品本身的物理化学性能衰变、润滑效果变差，并导致设备腐蚀[1]。基于数值计算的计算流体力学(CFD)方法正在冲击并改变着传统的工业过程设计方法，这对于油水两相分离的理论研究具有很重要的意义。

1 水力瞬变分析模型

液体管道通常受各种原因影响发生水力瞬变，而在水力瞬变过程中可能产生过高或过低的压力，严重时会对管道及其附属设备造成破坏[2]。水力瞬变分析模型是将油水两相流视为混合均匀的均质流体建立流体的基本方程组[3]后参考边界条件进行数值求解和模拟。

水力瞬变分析模型的研究重点在于模型中的摩阻的处理方法。传统水力瞬变分析方法是假定发生水力瞬变时的壁面切应力与速度为定常值时的壁面切应力相同，利用成熟的稳态摩阻的计算公式对瞬变时的摩阻进行近似计算。

(1)

式(1)中：τw为瞬变流动时的壁面切应力；τ为瞬变流动过程中的壁面拟稳态切应力；ρ为乳化液的密度(同下)；f为油水两相与管壁的摩阻因数(同下)；V为管内流体平均流速。

为了提高摩阻的准确度，Taitel等人在计算管内流体与管壁间的剪切应力时，认为摩阻因数与管内流体的雷诺数有关，采用勃拉休斯公式的形式表示。许多学者采用此法计算流体与管壁间的切应力。

(2)

Haland等人[4]认为，当管内流体处于紊流流态时，管壁粗糙度对摩擦阻力有一定影响。

(3)

式(2)中：Re为雷诺数；e为管壁粗糙度；Dh为水力直径。

水力瞬变分析模型使用非常广泛，常被应用于液体输送管道的水击的产生及防预研究[5]和研究管流水力瞬变过程中线路水力坡降线及某些水力参数的变化情况[6]等方面。吴峰平[7]基于水力瞬变分析模型推导出了适用于研究管道中油水乳化液的流动情况的水击谐波一维非恒定流模型，为水击谐波破乳奠定了理论基础。水击瞬变分析模型不需要求解庞大的线性或非线性方程组，易于求解。但其时间步长和管段步长的比值要受到一定稳定条件的限制，为满足求解的数值稳定性，时间层次往往只能取得很小。且工作量很大，依靠手工计算时无法完成的，必须借助计算机。

2 雷诺应力模型(RSM)

油水旋流分离器被广泛的应用于油水分离，具有结构简单，分离效率高的优点。为了能够达到更好的分离效率，关于油水旋流分离器的模拟和结构优化设计的研究与日俱增。湍流模型是油水旋流分离器模拟计算的核心，雷诺应力模型(RSM)是CFD程序中最精细的湍流模型。雷诺应力模型是由雷诺应力输运方程和基本方程组形成的封闭雷诺应力方程组。其基本方程组由混合液的连续性方程和动量方程组成，对于等温条件下流动的油水混合液有：

连续性方程为

(4)

动量方程为

(5)

po=pw

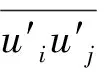
雷诺应力方程经过模化后为[8,9]：

(6)

式(6)中，等式左端两项分别为应力随时间的变化率和对流项；Dij为湍流扩散项；Pij为应力产生项；Φij为压力应变项；εij为粘性耗散项；xk为笛卡尔坐标分量；uk为速度时均速度分量。

(7)

(8)

(9)

(10)

式(10)中，μt为湍动黏度；σk为湍动能对应的Prandt1数，σk=0.82；C1和C2为模型常数；k为湍动能，ε为湍能耗散率，δij为“Kronecker delta”符号。

经过模型化以后，能够得到相应的湍动能方程和湍动能耗散率方程，再基于边界条件就能够求解模型，从达到数值模拟油水旋流分离器内油水分离的情况。牛贵锋等[10]利用雷诺应力模型CFD数值模拟方法得到了油水旋流分离器的流量-分离效率曲线、分流比-分离效率曲线、流量-压力降曲线及粒级效率分离曲线。雷诺应力模型严格地考虑了流线型弯曲、旋涡、旋转和张力快速变化，能很好的表示出湍流各向异性，从而能准确的描述旋流器流场内的实际流动情况。但雷诺应力再分配项不是十分精确，有待研究更加精确的模化方式。

3 双流体模型

双流体模型产生于20世纪70年代，将油水两相看作是时空上共存具有各自的容积分数并可以互相渗透的连续介质。采用双流体模型建立两相流方程的观点和基本方法是，先建立每一相的瞬时的、局部的守恒方程，然后采用某种平均的方法得到两相流方程和各种相间作用的表达式[11]。其优点在于能够较全面地考虑分散相的湍流输运，其数值模拟的结果也易于检验。双流体模型的一般表达式为[12-14]:

连续方程：

(11)

动量方程:

(12)

式(12)中，αk为油水两相的体积分数，当k=o时表示油相，k=w时表示水相，且αw+αo=1(同下)；uki为两相的速度分量；ρk为两相的密度；Fki分别为油水两相所受的作用力，Fwi=-Foi；τki、τTki分别为两相的黏性应力及紊动应力，pk为两相的静压强。

根据po、pw之间的关系，双流体模型可分为等压双流体模型和双压双流体模型，通常使用的双流体模型为等压双流体模型即po=pw。Foi、Fwi所受的作用力主要是油水两相间的作用力，包含黏性阻力、附加质量力、Basset力、Magus升力、Saffman升力等[15]。相间作用力非常复杂，为了便于计算，在不考虑近壁的影响时，Magus升力和Saffman升力均可不计[16]。附加质量力和Basset力也因形式比较复杂而在两相流计算中常被忽略。因此，相间作用力只包含黏性阻力[17,18]即：

(13)

式(13)中，dw为水相颗粒的直径(同下)；CD为阻力系数(同下)。

双流体模型的变量较多，需要计算油水两相间的相互作用力，这些作用力比较复杂，为模型的求解增加了不好难度。双流体模型在油水分离中应用的比较少，主要被用于液固两相流的研究中。

4 代数滑移混合模型(ASM)

代数滑移混合模型将油水两相系统看作是混合体系，考虑了两相间的相对运动的代数关系，油水两相间不相溶也没有分间面，但两相之间可以互相穿透。模型由混合液的连续方程和动量方程，通过分散相的连续方程推导的分散相体积分数方程，表示两相间的相对运动的相对速度代数方程，以及使模型封闭的两相混合湍流动能k方程和湍流动能耗散率ε方程组成。代数滑移混合模型特别适用于在重力、离心力或其他体积力作用下粒子或液滴的分离计算[19]。

ASM模型的控制方程为[20，21]:

混合液的连续性方程：

(14)

混合液的动量方程：

(15)

分散相体积分数方程：

(16)

相对速度代数方程：

(17)

式(17)中：udo,i、udw,i分别表示油水两相的拖曳速度，Fj为体积力；uow为油水两相滑移速度；a为分散相水相的加速度。

通过建立乳化液中水相的运动方程可以得到水相的加速度，不考虑近壁的影响和附加质量力和Basset力后得到：

(18)

将模型化简并进行无量纲化处理后就能得到完整的代数滑移混合模型，结合边界条件和初始条件就可以进行数字求解。代数滑移混合模型跟双流体模型相比变量较少，它是将混合液看着是一个整体，不用计算油水两相间的相互作用力，能有效的避免双流体模型带来的缺点，减少误差。白志山等[22]采用代数滑移混合模型对旋流管内的旋转湍流流场进行了数值模拟，获得旋流管内的浓度分布、滑移速度和粒级效率曲线，并进一步验证了代数滑移混合模型应用于油水分离的正确性。

5 结论及建议

综上所述，虽然基于数值计算的计算流体力学方法研究油水分离已经获得了一些成功，但还有许多问题有待解决，建议今后着重发展方向为：将水力瞬变分析模型与计算机相结合来进行数值求解；研究更加精确的模化方式来完善雷诺应力模型中的再分配项；在双流体模型中，继续深入研究压力模型；进一步研究其他完整模型的数值计算方法。

参考文献：

[1] 李春燕,莫婉玲,廖泽斌,等.润滑油中微量水分的气相色谱分析[J].润滑与密封,2013,38(9):85-87

[2] 王学方,叶宏开,汤荣铭.工业管道的水锤[M].北京:科学出版社,1995

[3] 斯特里特.瞬变流[M].北京:水利电力出版社,1983

[4] HADZIABDIC M, OLIEMANS R V A. Parametric Study of A Model for Determining the Liquid Flow-rates from the Pressure Drop and Water Hold-up on Oil-water Flows [J]. International Journal of Multiphase Flow, 2007, 33(12): 1 365-1 394

[5] 陈崑,曾祥炜,陈巍,等.智能控制压力管道爆破保护系统的水击分析[J].液压与气动,2010(1):45-47

[6] 刘刚,蒲家宁.长输管道水力瞬变仿真[J].油气储运,2000,19(3):16-19

[7] 吴峰平.油包水型乳化液水击谐波破乳动力学分析及其机理研究[D].重庆：重庆工商大学,2011

[8] 赵立新,崔福义,蒋明虎,等.基于雷诺应力模型的脱油旋流器流场特性研究[J].化学工程,2007,35(5):32-35

[9] 刘海生,艾志久,刘春全.油水分离旋流器流场和分离性能的数值模拟[J].石油矿场机械,2006,26(6):26-29

[10] 牛贵锋,艾志久,刘春全,等.油水旋流分离器流动机理和分离性能研究[J].石油矿场机械,2007,36(9):13-16

[11] 张政,谢灼利.流体-固体两相流的数值模拟[J].化工学报,2001,52(1):1-11

[12] 赵琴,李嘉.水库浑水异重流的两相流模型适用性研究[J].水动力学研究与进展,2010,25(1):76-83

[13] 张宏伟,谭立新,陈刚，等.水气二相流双流体模型研究现状[J].陕西水力发电,2001,17(4):15-18

[14] 李东霞,徐旭,蔡国飙，等.火箭发动机气体-颗粒两相流双流体模型研究[J].固体火箭技术,2005,28(4):238-243

[15] 赵琴.浑水异重流两相流模型的比较研究[J].西华大学学报：自然科学版,2012,31(3):100-104

[16] ISHILL M, MISHING K. Two-fluid Model and Hydrodynamic Constitutive Relations[J].Nucl. Eng&Des,1984,82:107-126

[17] YU M H, XU J, WAN Y Y. Simulation and Dynamics Visualization of Flow and Sediment Motion Down Stream of Cuijiaying Dam[J].Journal of Hydrodynamics, 2006,18(4):492-498

[18] JIN S Y, LIU Y Z, WANG W Z. Numerical Evaluation of Two-fluid Mixing in A Swirl Micromixer[J].Journal of Hydrodynamics, 2006,18(5):542-546

[19] 李玉星,冯叔初.油水分离用水力旋流器理论模型及数值模拟[J].石油机械,2000,28(11):26-29

[20] 李永,李嘉,安瑞冬.水沙两相流ASM模型在浑水异重流计算中的应用及模型试验研究[J].四川大学学报：工程科学版,2009,41(4):102-107

[21] 周新民,赵文谦,李嘉.利用相间滑移考虑固相泥沙沉降效应[J].水动力学研究与进展,2004,19(5):593-597

[22] 白志山,汪华林.油滴在旋流分离中的相间滑移数值模拟[J].华东理工大学学报：自然科学版,2006,32(11):1355-1359.