一类非线性退化时滞微分系统的一致稳定性*

陈爱珍， 周宗福

(安徽大学 数学科学学院，合肥 230601)

0 引 言

微分系统的稳定性一直是微分方程领域的一个重要研究课题.近年来，有关退化时滞系统稳定性问题已引起许多学者的兴趣，取得了一定的成果.文献[1]根据退化系统特点提出了退化时滞微分系统解的“q”稳定概念，文献[3]利用退化时滞系统的拉什密辛型定理讨论了线性退化时滞微分系统解的稳定性，给出了零解稳定的一个判定定理.

在上述文献基础上，研究如下的一类非线性退化时滞微分系统的一致稳定性：

(1)

(2)

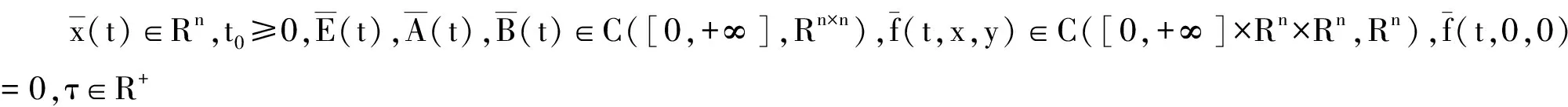
1 预备知识

其中I1，I2分别为n1阶及n-n1阶单位阵，A1(t)∈Rn1×n1，n1与t无关.

(3)

其中

初始条件(2)变为

(4)

研究思路是先研究系统(3)(4)的一致稳定性，然后得到系统(1)(2)的一致稳定性.

下面引进退化时滞微分系统解的稳定性的有关概念.考虑退化时滞微分方程

(5)

其中E为n×n奇异常数矩阵，t≥t0≥0，τ>0，x(t)∈Rn，xt(θ)=x(t+θ)(θ∈[-τ，0])，f(t，ψ)：[0，+∞)×H→Rn，H为C([-τ，0]，Rn)中一开集，f连续，f(t，0)=0，方程(5)的初始条件为

xt0=φ，φ∈C([-τ，0]，Rn)

(6)

定义1 (i) 若∀t0∈Tk，∀ε>0，总存在δ(t0，ε)>0，使得∀φ∈B(0，δ)∩Sk(t0，tk)，方程(5)过初始条件(t0，φ)的解x(t)=x(t，t0，φ)满足‖q(t，x(t))‖<ε，∀t∈[t0，tk)，则称方程(5)的零解关于{q(t，x)，Tk}为稳定的.

(ii) 若在(i)中，δ仅与ε有关，与t0无关，则称方程(5)的零解关于{q(t，x)，Tk}为一致稳定的.

下面给出拉什密辛型定理(Razumikhintheorem).

引理1[2]若存在连续可微的V函数V(t，y)：[0，+∞)×D→R+(D为Rm中一个开集)，及函数φ1(s)，φ2(s)：R+→R+，φ1(0)=0，φ2(0)=0，φ1(s)，φ2(s)在R+上连续且严格单调递增，满足

1) φ1(‖q(t，x)‖)≤V(t，q(t，x))≤φ2(‖x‖)；

2 主要结果

定理1 对于方程(3)，若以下条件满足

1) ∃M>0，‖B21(t)‖≤M，∀t≥0；

2) ∃q0：0

从而

(1-l2)‖x2(t)‖≤(‖B21(t)‖+l2)‖x1(t-τ)‖+(‖B22(t)‖+l2)‖x2(t-τ)‖+l2‖x1(t)‖

即有

一直递推下去，必存在k使得t-kτ∈[t0-τ，t0]，从而可得

进一步地，有

从而引理1中的条件2)满足.

定理2 在定理1的条件下，方程(3)的零解关于{x，[0，+∞)}为一致稳定的.

从而

如此递推下去，必存在k，使得t-kτ∈[t0-τ，t0]，从而可得

因此，方程(3)的零解关于{x，[0，+∞)}为一致稳定的.证毕.

设Q∈Rn×n为对称阵，用λmin(Q)表示Q的最小特征值.

又由于

从而方程(1)的零解关于{x，[0，+∞)}是一致稳定的.证毕.

参考文献：

[1] 李远清，刘永清.广义泛函微分方程解的稳定性[J].应用数学学报，1999，22(1)：130-138

[2] 李远清，刘永清，陆以勤.一类滞后时变广义微分系统稳定性的拉什密辛型定理[J].控制理论与应用，1999，16(2)：235-237

[3] 韩仁基，蒋威.变系数退化时滞微分系统解的稳定性[J].数学研究，2008，41(4)：401-406

[4] MARZ R. Some New Results Concerning Index-3 Differential-algebraic Equations[J]. J Math Anal Appl，1989，140(1)：177-179