一种带强Wolfe线搜索的CD和LS混合共轭梯度算法*

马 烁

(荆州理工职业学院， 湖北 荆州 434000)

0 引 言

考虑无约束优化问题

(1)

其中f：Rn→R连续可微.

共轭梯度法是求解无约束优化问题(1)的一类有效算法，它的迭代公式形如

xk+1=xk+αkdk

(2)

其中，αk由某种线性搜索决定，dk为第k次搜索方向，由式(3)计算

(3)

共轭梯度法的关键是选取αk和βk，不同的αk和βk决定了不同的共轭梯度算法.βk的选取公式常用的有

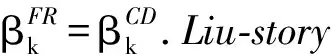
采用强Wolfe线搜索，受文献[7-11]的启发，步长因子αk同时满足

(4)

(5)

其中δ和σ是满足0<δ<σ<1/2的常数.结合CD方法和LS方法提出了一类具有良好收敛性和数值表现的混合共轭梯度法.在强Wolfe线搜索下，证明了算法具有下降性，并给出了算法具有全局收敛性的证明，数值结果表明算法的有效性.此处提出一类新的βk公式

(6)

1 新的共轭梯度算法及其下降性

为了后面证明的需要，给出假设H：

(i) 水平集L1={x∈Rn|f(x)≤f(x1)}有界，其中x1为初始点；

(ii) 在水平集L1的一个邻域U内，f(x)是连续可微的，其梯度g(x)是lipschitz连续的，即存在常数L>0，使

‖g(x)-g(y)‖≤L‖x-y‖，∀x，y∈U

(7)

求解无约束问题的新算法NCDLS.

步1 给定初始点x1∈Rn，ε>0，d1=-g1，令k：=1；

步2 若‖gk‖≤ε，则停止迭代；否则，由强Wolfe线搜索式(4)、式(5)计算步长因子αk，计算xk+1=xk+αkdk，k：=k+1；

步3 利用式(6)计算βk+1，计算dk+1=-gk+1+βk+1dk，置k：=k+1，转步2.

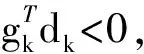
证明用数学归纳法证明.

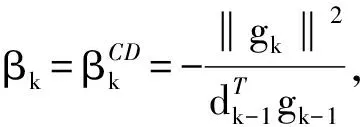
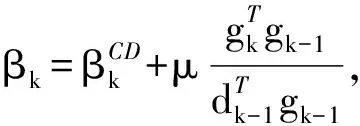
由式(5)，有

2 新算法的全局收敛性分析

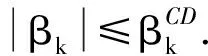
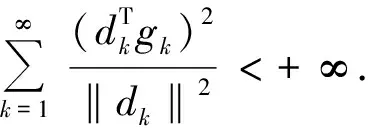
(8)

对式(8)从k=1，2，…求和并考虑假设条件H，即得引理2.

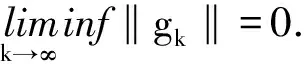
证明由式(3)得 dk+gk=βkdk-1，两边同时取平方得

(9)

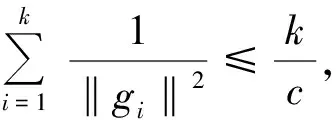
3 数值试验

用文献[12]，[13]中的测试函数检验本算法，并将结果与标准CD方法和标准LS方法进行比较.所有实验均采用强Wolfe线搜索，均不采用重新开始策略.测试环境为MATLAB7.9.0，运行环境为内存4.00 GB，CPU为2.60 GHz的个人计算机.参数设置如下：δ=0.1，σ=0.45，μ=0.9，终止条件为‖gk‖≤10-6或It-limit>9 999，计算得到3种方法的数值结果如表1所示.

表1中“Prolem”表示测试函数的名称，“DIM”表示测试函数的维数 “NI/NF/NG/T”依次表示迭代的次数、函数值计算的次数、梯度值计算的次数及CPU计算时间，“F”表示迭代失败.

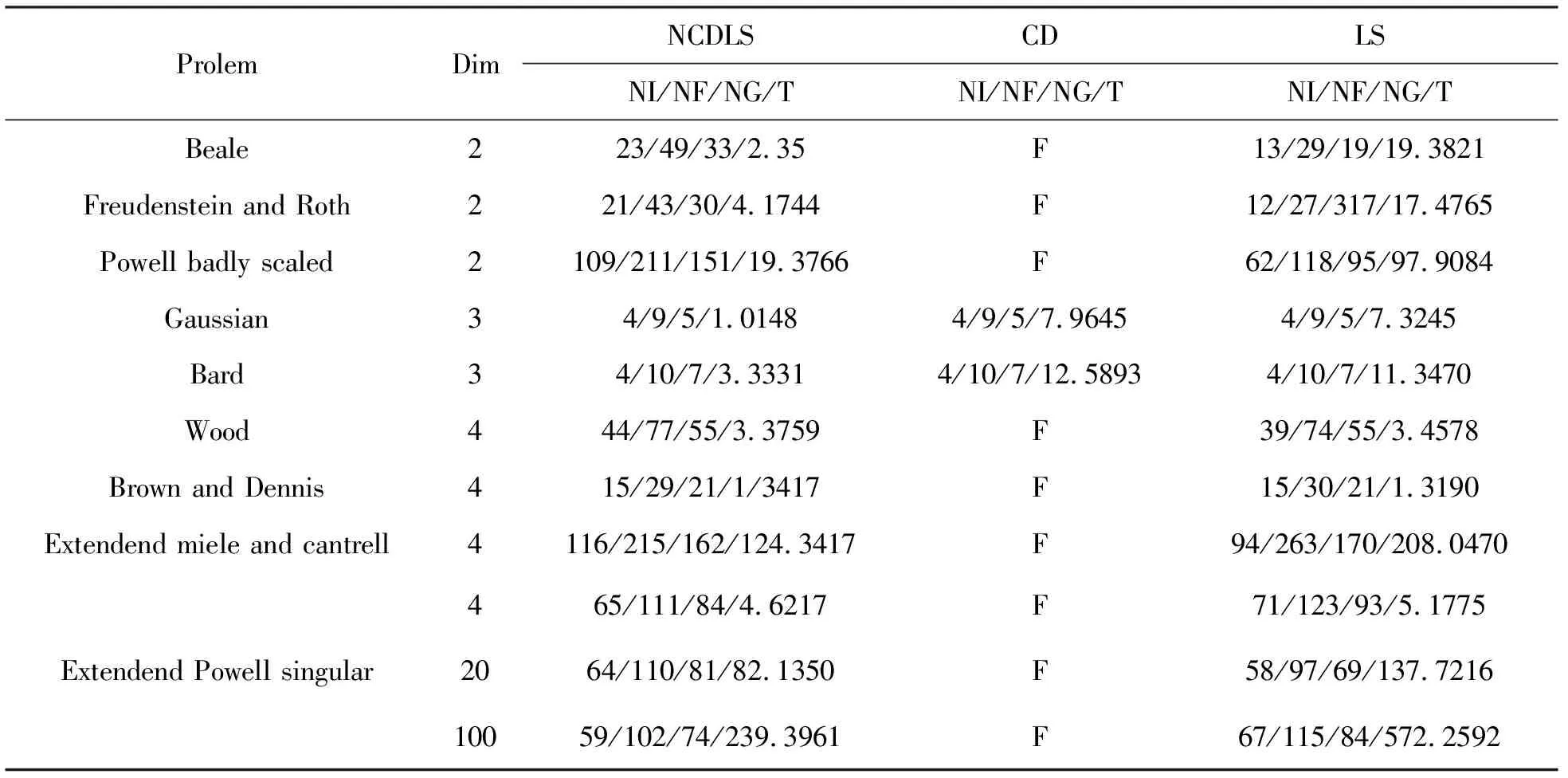
表1 数值测试结果及其比较

通过对7个问题的测试可以看出，此处提出的NCDLS算法的CPU时间要比LS方法少，对于最后一个测试函数，该算法总体要比LS好很多，而CD方法几乎都失败了，这是因为CD方法产生连续的小步长而无法恢复.所测试的函数均能说明新方法的可行性.但为了能得到更好的数值效果，还需要进一步研究方法中参数的选取和搜索条件的选择.实验结果显示，该算法是有效的.

参考文献：

[1] FLETCHER R，REEVES C.Function Minimization by Conjugate Gradients[J].Computer Journal，1964(7)：149-154

[2] POLAK E，RIBIERE G.Note Sur La Convergence De Dirctions Conjugees[J].Rev Fran-caise Informat Recherche Opertionelle，3e Annee，1969(16)：35-43

[3] HESTENES M R，SRIEFEL E L.Methods of Conjugate Gradient for Solving Linear Systems[J].Journal of Research of the National Bureau of Standards，1952，6(49)：40-43

[4] FLETCHER R.Practical Methods Optimization[C]∥John Wiley&sons：Unconstrained optimization.New York，1987

[5] LIU Y，STOREY C. Effcient Generalized Conjugate Gradient Algorithms[J].Journal of Optimiztion Theory and Applicatons，1991，69：129-137

[6] DAI Y H，YUAN Y. A nonlinear Conjugate Gradient with A Strong Global Conver-gence Property[J].SIAM Journal on Optimizton，2000(10)：177-182

[7] 王开荣，曹伟，王银河.Armijo型线搜索下的谱CD共轭梯度法[J].山东大学学报：理学版，2010，45(11)：104-108

[8] 李敏.改进的LS共轭梯度法及其收敛性[J].怀化学院学报，2011，30(8)：1-4

[9] 王董晓亮.Armijo搜索下改进的LS共轭梯度法[J].陕西理工学院学报：自然科学版，2013，29(3)：49-53

[10] 敖卫斌.一种修正的DY共轭梯度法的全局收敛性[J].重庆工商大学学报：自然科学版，2013，30(10)：17-20

[11] 张雁，单锐，王换鹏，等.一类混合CD-LS共轭梯度法的全局收敛性[J].辽宁工程技术大学学报：自然科学版，2013，32(3)：409-412

[12] MORE J J，GARBOW B S，HILLSTROME K E.Testing Unconstrained Optimization Software[J].ACM Trans Math Software，1981(7)：17-41

[13] WOLFE M A.Numerical Methods for Unconstrained Optimization[M].An Introduction，Van Nostrand Reinhold，London，1978