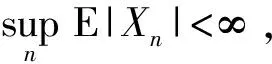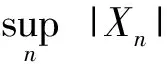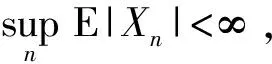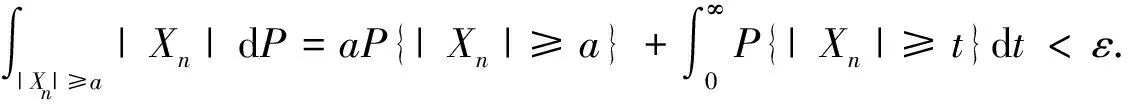随机变量序列的一致可积条件探索*

张 培， 任春光， 王学军

(1.郑州华信学院 基础教学部，郑州 451100；2.安徽大学 数学科学学院，合肥 230601)

随机变量序列的一致可积概念与种种收敛性问题的讨论有着密切关系，因此有必要研究何时随机变量序列是一致可积的.直接验证随机变量序列的一致可积往往是不容易的，故此处主要研究一致可积成立的充分条件，由这些条件比较容易验证一致可积性.相关不等式的证明参见文献[1]，基于贝叶斯相关理论参见文献[2].有关随机变量的其他一些性质，如最大值不等式及大偏差的结果，可参见文献[3]，随机变量的Hájek-Rényi型不等式和其收敛速度见文献[4]和文献[5]，非负随机变量序列的逆矩问题参见文献[6]，随机变量序列的强收敛速度问题可参见文献[7]，推广的Borel强大数定律的改进的可以参见文献[8].记r.v.为随机变量；c0，c1，c2，c3，c4，c均为常数；Xn为r.v.；Ω为样本空间；F为事件域.

1 预备知识

引理1[9]r.v.序列{Xn}是一致可积的充要条件是

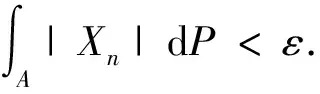
由引理1可以得出下述两个关于一致可积的充分条件.

引理3[9]设有r.v.Y，E|Y|<∞，且对任何正实数a，满足P{|Xn|≥a}≤P{|Y|≥a}，则r.v.序列{Xn}是一致可积的.

引理4[10](积分中值定理) 设f，g是测度空间(Ω，F，μ)上的可测函数，g关于μ可积，-∞

引理5(积分中值定理的推广) 设f，g是测度空间(Ω，F，μ)上的可测函数，g关于μ可积，-∞

2 主要结论及其证明

定理1是引理1的改进，优点在于定理1只能用于{Xn}的大于1阶的绝对原点矩的情形，后者可以用于大于0阶的绝对原点矩的情形.

对任意的ε>0，可选适当的a，使得

参考文献：

[1] 曾静.不等式证明的三种方法[J].重庆工商大学学报：自然科学版，2013，30(7)：16-18

[2] 王筱薇青.基于贝叶斯相关理论的最佳阈值分割图像处理[J].重庆工商大学学报：自然科学版，2013，30(3)：55-57

[3] 李晓琴，胡舒合，王学军，等.M-Z型序列的最大值不等式和大偏差定理[J].安徽大学学报：自然科学版，2010，34(3)：5-9

[4] 赵婷，胡舒合，李晓琴，等.一类随机变量的概率不等式及几乎处处收敛性[J].安徽大学学报：自然科学版，2010，34(1)：7-10

[5] 胡舒合，胡晓鹏，张林松.二阶矩限制下的Hajek-Renyi型不等式及其应用[J].应用数学学报，2005，28(2)：227-235

[6] 胡舒合，陈桂景，王学军，等.关于弱收敛非负随机变量序列的逆矩[J].应用数学学报，2007，30(2)：361-367

[7] 胡舒合.强大数定律的若干新结果[J].数学学报，2003，46(6)：1123-1134

[8] 任春光，胡舒合，李旭，等.一个推广的Borel强大数定律的改进 [J].安徽大学学报：自然科学版，2011，35(3)：25-28

[9] 林正炎，陆传荣，苏中根.概率极限理论基础[M].北京：高等教育出版社，2006

[10] 严士健，王隽骧，刘秀芳.概率论基础[M].北京：科学出版社，2009