基于Laplace分布和CVaR的投资组合模型研究*

张永芬， 张令元

(上海开放大学 金融会计系，上海 200433)

现代投资组合理论主要研究在未来结果不确定的情况下怎样对有限的资产进行投资，使得预期收益和风险达到合理的均衡[1].风险价值VaR(Value-at-Risk)和条件风险价值[2，3]CVaR(Conditional Value-at-Risk)是近年来盛行的金融资产的风险评价工具，CVaR由于是一致性风险度量方法，满足凸性、正齐次性，已经成为金融风险度量的有力工具.

近年来国内在风险价值度量方面的研究较热，且大都是假设金融资产的收益率服从正态分布.刘小茂、姚慧丽等研究了正态分布下均值-CVaR有效前沿[4，5].高岳琳、李婷等研究了基于CVaR约束的单位风险收益最大投资组合模型[6]和均值-CVaR的算法分析[7].杨梅等研究了模型期望值证券投资组合模型[8].由于Lapalce分布具有明显的尖峰厚尾性，运用Laplace分布来对金融数据进行拟合，能很好地描述这一性质[9].此处以CVaR为风险度量工具，引入Laplace分布，研究Laplace分布下的均值-CVaR投资组合模型.

1 Laplace分布概述

1.1 Laplace分布[10]

1.2 Laplace分布的性质

如果X服从LA(μ，σ)，则

(2) E(X)=μ，Var(X)=2σ2.

1.3 LA(0，1)分布与N(0，1)分布的图形

从图1可见Laplace分布比正态分布有更厚的尾部和更尖的峰度.

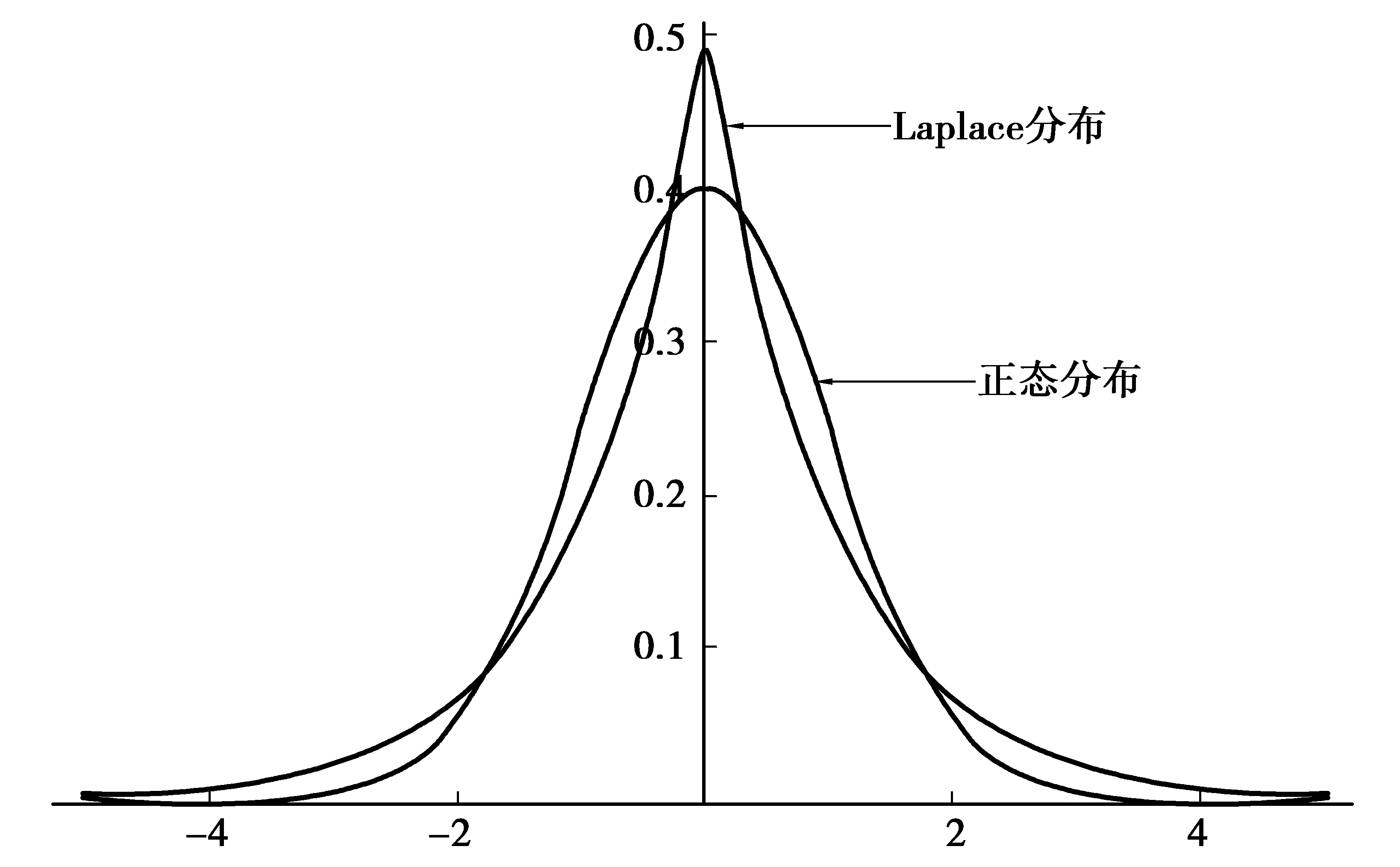
图1 Laplace分布和标准正态分布的概率密度

2 投资组合VaR和CVaR的计算

2.1 VaR和CVaR定义

定义2 VaR和CVaR的数学定义可表示如式(1)(2)

p(Y>VaRβ)=1-β

(1)

CVaRβ=E[Y|Y>VaRβ]

(2)

其中Y为某金融资产的损失，是个随机变量，β为给定的概率置信度.

设x=(x1，x2，…，xn)T为n种资产的投资比例向量，y=(y1，y2，…，yn)T为n种资产的收益率.假设p(y) 为向量y的密度函数，设f(x，y)为组合的预期损失函数，则对任意的a∈R，损失f(x，y)不超过a的概率为

则对任意的置信水平β∈(0，1)，有

2.2 VaR的计算

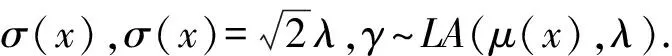
由VaR的定义：p(γ>VaRβ)=1-β，所以

(3)

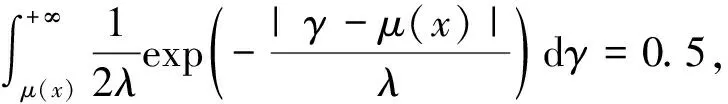
(4)

可得

VaRβ=μ(x)-λln(2(1-β))

(5)

2.3 CVaR的计算

(6)

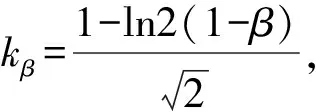
CVaRβ=μ(x)+kβσ(x)

(7)

3 均值-CVaR模型的建立及求解

3.1 模型建立

设rx=xTy为投资组合的收益，f(x，y)=-xTy为投资组合的损失，假设E(y)=μ，Cov(y)=V，V是正定矩阵，则可得到E(rx)=xTu和方差Var(rx)=xTVx.记E[f(x，y)]=-E(rx)，σ2(rx)=Var(f(x，y))=xTVx，收益率约束可以表述为E(rx)=xTu=R，其中R为投资者预先设定的期望收益，在满足预期收益为R的条件下，使投资组合的CVaR最小.投资比例约束为

基于以上假设及计算，可以得到均值-CVaR投资组合优化模型

min CVaRβ=kβσ(rx)-E(rx)

(8)

3.2 模型求解

文献[7]给出了正态条件下模型有解的条件，下面构造Lagrange函数对模型(8)进行求解：

(9)

求解式(9)，并令A=μTV-1I，B=μTV-1μ，C=ITV-1I，D=BC-A2，且B>0，C>0，D>0，解得

(10)

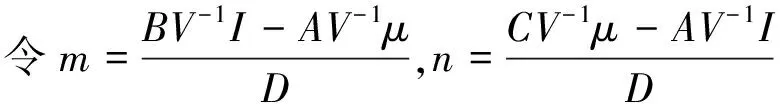
(11)

则式(10)成为

x=m+nE(rx)

(12)

(13)

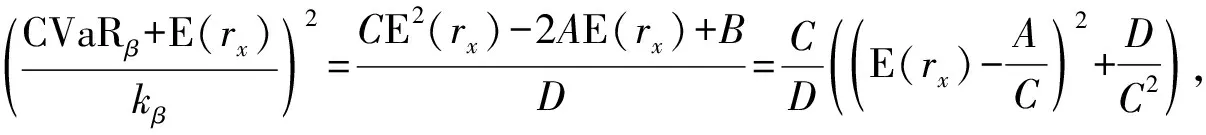
(14)

所以，均值-CVaR模型的边界曲线在均值-CVaR坐标系下是一条开口向右的双曲线(开口向左的曲线舍去)，曲线AB为均值-CVaR有效前沿.

图2 均值-CVaR边界和有效前沿

3.3 求解最小CVaR

定理1 若在给定置信水平β(0<β<1)下的最小CVaRβ组合存在，则它必位于均值-方差有效前沿上.

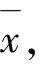
即对任意给定的β，组合x的CVaR不是最小，故x不是最小CVaR组合.

(15)

所以求解最小CVaR等价于求下列优化问题

(16)

(1) CVaRβ对σ(rx)的一阶导数为

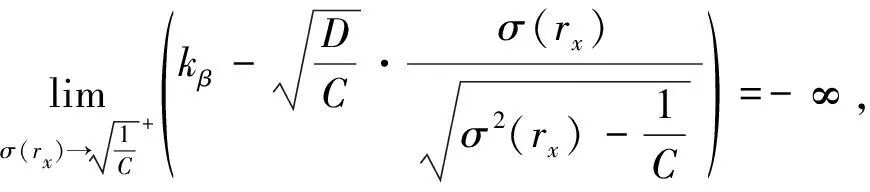
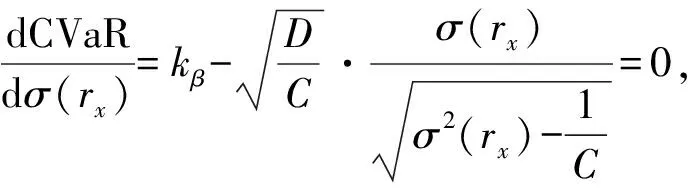
(17)

(18)

(19)

其中m，n的定义同式(9).

4 实证分析

随机选取沪深股市中收益比较好的4只股票步步高、贝因美、浦东金桥、上海电气进行标的资产配置，并将它们编号为A、B、C、D.选取的数据为2011年5月至2011年10月101个交易日的日收盘价收益率数据作为历史收益率情景，来计算各个股票的日收益率的均值和它们的协方差，如表1、表2所示.考虑到期内可能有派息、分红，所有的数据都是还权后得到的(此处的计算采用Matlab2010a，Excel 2007和R统计软件).

4.1 股票的连续复利收益率的均值和方差-协方差矩阵的计算

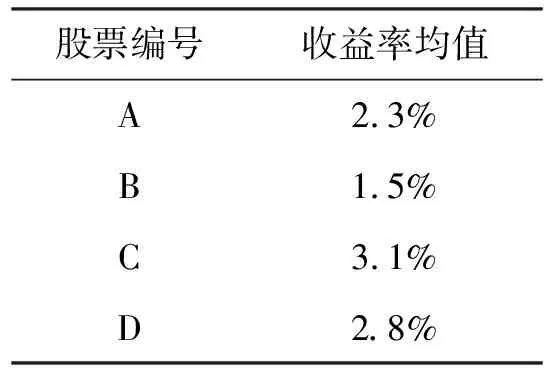
表1 各资产收益率的均值

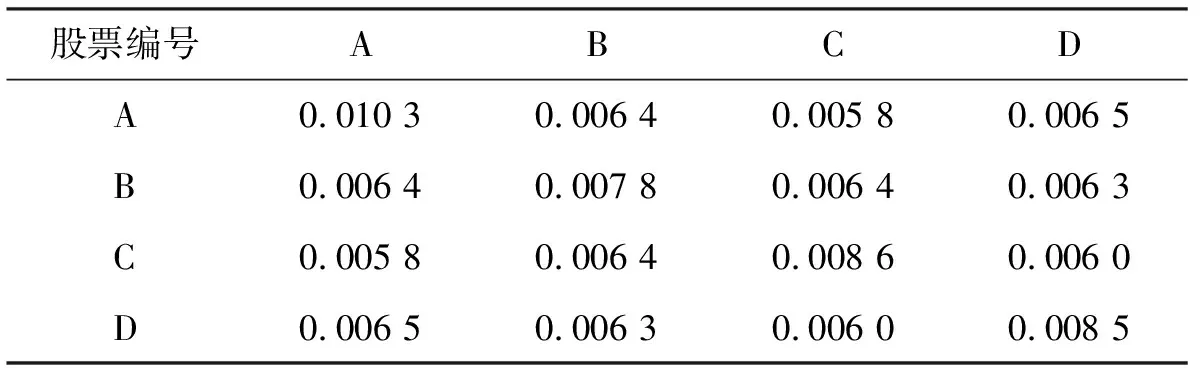
表2 各资产收益率的方差-协方差矩阵V

4.2 全局最小化CVaR及最优解计算

取β=95%，则kβ=2.33，A=μTV-1I，B=μTV-1μ，C=ITV-1I，D=BC-A2，计算模型中各字母的值如下

A=3.515 8，B=0.175 3，C=146.638 0，D=13.339 8

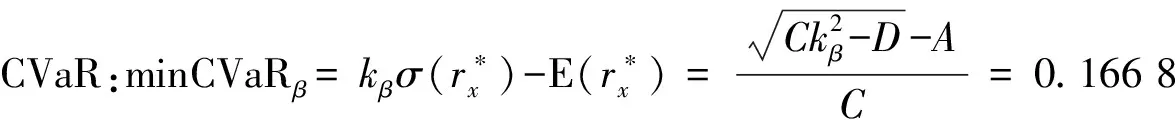
4.3 正态分布与Laplace分布下均值-CVaR有效前沿比较

Laplace分布下均值-CVaR边界方程为式(14)，正态分布下均值-CVaR边界方程为[4]

(20)

Laplace分布下均值-CVaR模型最优期望回报和最小CVaR分别为式(17)和式(18)，正态分布下均值-CVaR模型最优期望回报和最小CVaR分别为

(21)

(22)

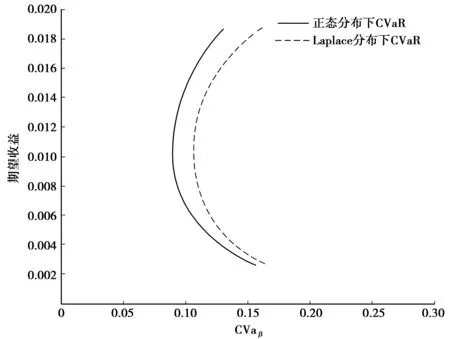
图3 正态分布和Laplace分布均值-CVaR有效前沿

5 结束语

条件风险价值CVaR是风险价值VaR的修正，它比VaR具有更好的性质，Laplace分布比正态分布更能拟合金融资产的实际回报率.同时引入CVaR和Laplace约束，建立了均值-CVaR模型，得到了模型的有效边界、最优解和有效前沿的表达式.最后采用沪深股市的4只股票进行实证研究，计算出了最优投资比例和相对应的风险，并与正态分布下的均值-CVaR模型进行了比较研究.从理论上丰富了投资组合理论，考虑不同分布、不同风险度量标准下的风险管理，在实践中对投资者进行投资决策也有很强的指导意义.

参考文献：

[1] MARKOWITZ H M.Portfolio selection[J].Journal of Finance，1952，7(1)：77-91

[2] TYRRELL R，STANISLAV U .Optimization of Conditional Value-at-Risk[J].Journal of Risk，2000，2(3)：21-42

[3] TYRRELL R，STANISLAV U.Conditional Value-at-Risk for general loss distributions[J].Journal of Banking & Finance，2002，26：1443-1471

[4] 刘小茂，李楚霖，王建华.风险资产组合的均值-CVaR有效前沿(Ⅰ)[J].管理工程学报，2003，17(1)：29-32

[5] 姚慧丽.均值-CVaR投资组合有效边缘的灵敏度分析[J].统计与决策，2010(19)：65-67

[6] 高岳琳，陈东志，鲍卫军.基于CVaR约束的单位风险收益最大投资组合模型及实证[J].统计与决策，2009(13)：62-64

[7] 李婷，张卫国.风险资产组合均值-CVaR模型的算法分析[J].安徽大学学报：自然科学版，2006，30(6)：34-37

[8] 杨梅，卢伦慧.模糊期望值证券投资组合模型研究和实证分析[J].重庆工商大学学报：自然科学版，2013，30(3)：22-28

[9] 唐林俊，杨虎.沪深股市收益率分布特征的统计分析[J].数理统计与管理，2003，23(5)：1-4

[10] 杜红军，刘小茂.拉普拉斯分布下的VaR和CVaR风险计算[J].应用数学，2006(19)：225-228