模糊综合评判在高职院校奖学金评定中的应用

孙文鑫， 卓春英， 王国栋

(重庆水利电力职业技术学院，重庆 永川 402160)

模糊数学[1]是一门发展很快的学科，为其做出奠定性贡献的是美国控制论专家L.A. Zadeh，于1965年在杂志Information and Control上发表了一篇著名的论文，标志着模糊理论的产生，模糊数学在实际中的应用广泛几乎涉及了国民经济的各个领域及部门，如医学、军事、社会治安、农业、气象、林业、环境、地质勘查等[1，2]。

模糊综合评判是模糊数学中一种既年轻又发展很快的数学建模方法。著名汪培庄教授[3]于20世纪80年代初期提出了对绿色供应链绩效进行评价的模糊综合评价模型。随着社会经济的高速发展，以及人们考虑问题的复杂性、不确定性以及人类思维的模糊性的不断增强，致使人们对事情的评价难以客观。因此应用模糊数学中的模糊综合评判来求解综合评判问题也越来越受到人们关注，国内外不少学者对模糊综合评判的方法进行了研究，并将这一评判方法广泛的应用到了各个领域，其中包括行业经济评价、海洋富营养化评价、生活质量评价、人员素质评价[4]、大气环境质量评价、可持续发展评价等领域[5-9]。

主要将模糊数学的综合评价应用到高职院校大学生奖学金的评价中.首先，确定了高职院校大学生奖学金评价的因素集、评价集以及权重。其次，采用问卷调查法计算出了各指标的模糊评价矩阵，建立了高职院校大学生奖学金的模糊综合评价模型。最后，运用最大隶属原则确定了模型的评价结果。

1 模糊综合评判模型

模糊综合评判是利用模糊线性变换原理和最大隶属度原则，考虑与被评价事物相关的各个因素，对其做出合理的综合评价。

一级模糊综合评价模型

定义1[10]设因素集U={u1，u2，…，un}，评价集V={v1，v2，…，vm}，权重集W=(w1，w2，…，wn)，f是从因素集U到F(V)的一个模糊映射：

称模糊映射f确定的模糊关系R∈μn×m为模糊评价矩阵。记为

rij表示因素集U中元素ui关于评价集V中元素vj的评价。

由权重矩阵与模糊评判矩阵R的乘积得到向量B为：

B=W∘R=(b1，b2，…，bm)

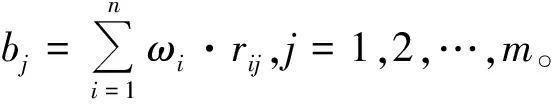
对B进一步“归一化”处理，即得：

其中

二级模糊综合评价模型

模型Ⅱ[15]

定义2[8]设Ai∈F(U)(i=1，2，…，n)，对于任意的u0∈U，若存在i0，使得

Ai0(u0)=max{A1(u0)，A2(u0)，…An(u0)}

则认为u0相对的隶属于Ai0，这就是最大隶属原则。

2 模糊综合评判法在高职院校奖学金评定方面的应用

为激励学生勤奋学习，各大高校设立奖学金评定制度。通过模糊综合评判法对高职院校奖学金做出合理公正的评定。

2.1 建立高职院校奖学金评价指标体系

根据高职院校在评奖学金时考虑的因素和指标，首先建立高职院校奖学金的评价指标体系如表1所示。

表1 职业高校奖学金评价指标体系

由表1可以得出德育、智育、体育、实践4个指标构成因素集，记作U={μ1，μ2，μ3，μ4}；此外，指标社会责任感、集体责任感、诚实守信构成了德育的因素集，记作μ1={μ11，μ12，μ13}；指标专业必修、专业选修、公共课构成了智育的因素集，记作μ2={μ21，μ22，μ23}；指标体育文化、体育技能、体育素养构成了体育的因素集，记作μ3={μ31，μ32，μ33}；指标校内实践和校外实践构成了实践的因素集，记作μ4={μ41，μ42}。

以上建立了高职院校奖学金评价的因素集，下面建立评价体系。

评价集是评价者对评价对象可能做出的各种各样的评价结果组成的集合，根据各职业高校的具体情况，将评价体系分为一等、二等、三等、无奖学金4个指标，记作

V={v1，v2，v3，v4}

其中v1表示一等奖学金；v2表示二等奖学金；v3表示三等奖学金；v4表示无奖学金。

2.2 权重的确定

权重是一个相对的概念，是针对某一指标而言.某一指标的权重是指该指标在整体评价中的相对重要程度.权重的计算方法主要有专家直观判定法、层次分析法和排序法.直接采用重庆某职业高校大学生奖学金评定办法规定的各项权重.具体各指标的权重如下：

ω=(ω1，ω2，ω3，ω4)=(0.1，0.6，0.1，0.2)

其中ω1表示德育的权重，ω2表示智育的权重，ω3表示体育的权重，ω4表示实践的权重.

其中ω11表示社会责任感的权重，ω12表示集体责任感的权重，ω13表示诚实守信的权重，ω21表示专业必修的权重，ω22表示专业选修的权重，ω23表示公共课的权重，ω31表示体育文化的权重，ω32表示体育技能的权重，ω33表示体育素养的权重，ω41表示校内实践的权重，ω42表示校外实践的权重。

2.3 模糊矩阵的确定

为了确保数据的合理性和有效性，采用问卷调查法对在校高职院校的学生奖学金的评定进行了调查研究，并对调查表进行整理和统计。然后通过统计出的评语cvi的频数计算出各指标的模糊评价矩阵(rij)，即：

其中m为调查问卷总数。

根据以上方法可计算出各指标的模糊矩阵如下：

首先根据统计结果计算得到德育的模糊综合矩阵为

智育的模糊综合评价矩阵为

体育的模糊综合评价矩阵为

实践的模糊综合评价矩阵为

2.4 模糊综合评价模型的建立

前面已经通过问卷调查法计算出了各指标的模糊评价矩阵，下面运用上面的结果建立模糊综合评价模型。首先建立高职院校奖学金评价的一级模糊综合评价模型。

根据模糊综合评价模型，建立德育的模糊综合评价模型如下：

其中B1是表示德育的评价集.

智育的模糊综合评价模型如下：

其中B2是表示智育的评价集.

体育的模糊综合评价模型如下：

其中B3是表示体育的评价集.

实践的模糊综合评价模型如下：

其中B4是表示实践的评价集.

其次，根据上面计算结果，将向量B1，B2，B3，B4构造成新的矩阵R如下：

建立高职院校奖学金评价的二级模糊综合评价模型如下：

最后根据最大隶属原则可以判断出学生应为一等奖学金。

3 结 论

运用模糊数学综合评判方法，通过确定影响高职院校大学生奖学金评价的因素，对高职院校大学生进行问卷调查，确定了影响奖学金评价的指标体系，计算出了各因素的模糊关系矩阵，建立了高职院校大学生奖学金的模糊综合评价模型。最后运用最大隶属原则，对学生做出了合理的评价。

参考文献：

[1] 陈亚娜，石磊. 模糊控制在混合煤气压力与热值控制中的应用研究[J]. 机电产品开发与创新，2008，21(1)：160-161

[2] 蒋德珑，尹淑萍，师黎，等. 基于模糊综合评判的研究生综合素质评价研究[J]. 计算机工程与设计，2011，32：3208-3212

[3] 汪培庄.模糊集合论及其应用[M].上海：上海科技出版社，1982

[4] 李柏年，模糊数学及其应用[M].合肥工业大学出版社，2007

[5] 陈伟伯，任秀芳，李腾龙.模糊评价法在国家奖助学金评定工作中的应用[J].技术与创新管理，2007(6)：72-73

[6] 邵世芳.基于模糊综合评判方法的大学生学习心理研究[J].经济研究导刊，2011，23：253-255

[7] 唐剑锋. 基于模糊综合评判的大学生消费结构分析[J]. 科技致富向导，2011，23：84-85

[8] 尹爱芹，李云，刘学诚，等. 模糊综合评判在教学质量评价中的应用研究[J]. 泰山学院学报，2011(3)：17-20

[9] 张佳瑜，闫丽媛，曹敏，等.高校大学生奖学金评定中的多指标模型研究[J].重庆工商大学学报，2010，27(2)：125-129

[10] 杨纶标，高英仪.模糊数学原理及应用[M].华南理工大学出版社，2008