基于有杆抽油系统Gibbs模型中泵功图的计算研究

杨 星 星

(宿州学院 数学与统计学院，安徽 宿州 234000)

首先给出抽油杆振动模型，再用模型推导由悬点示功图转化为泵功图的过程，包括原始数据处理、边界条件、初始条件、连接条件以及求解算法。

1 抽油杆振动模型

在一维情况下，有杆抽油系统模型就是指抽油杆的振动模型。模型包括：波动方程、上下边界条件、初始条件和连接条件(多级杆结构)。

1.1 波动方程

Gibbs提出了一维粘滞阻尼波动方程作为描述抽油杆运动和应力传播的基本微分方程。其方程[1]为

(1)

1.2 上下边界条件

模型的上边界条件由抽油机悬点运动规律所决定。设U(t)为悬点的位移函数，则模型的上边界条件为

u(x，t)|x=0=U(t)

(2)

模型的下边界条件由井下泵的工作状况决定。设Fp(t)为柱塞的载荷函数，则模型的下边界条件为

F(x，t)|x=L=Fp(t)

(3)

1.3 初始条件

假设系统在启动前，抽油杆从驴头上自由悬挂于充满液体的油管中，并且驴头从下死点开始向上运动，即初始时刻位移与速度均为零，则模型的初始条件[2]为

(4)

1.4 连接条件

对于多级杆柱结构，两杆连接处的载荷与位移连续条件应满足：上级抽油杆底端与下级抽油杆顶端的载荷、位移都是始终相等的，其数学关系式如下：

(5)

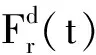
1.5 完整的数学模型

由式(1)-(5)构成了有杆抽油系统完整的数学模型，即：

(6)

2 模型求解

采用分离变量傅里叶变换法求解波动方程。

(7)

根据胡克定律，式(7)可写成：

(8)

波动方程上边界条件的傅里叶级数形式如下：

(9)

式中：N表示傅里叶级数的项数，取N=15；ν0，νn，δn，σ0，σn，τn(n=1，2，…，N)——傅里叶级数.

式(9)中的6个傅氏系数由实测的D(t)和U(t)曲线数值积分求得，由于给定数据是离散的，故采用梯形法则进行数值积分，下面以σn为例进行计算。

给出连续曲线数值积分公式：

(10)

(11)

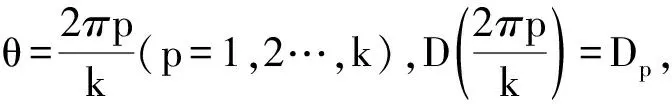
(12)

由函数的周期性可得：D0=Dk，cos0=cos2nπ，因此：

(13)

同理可求得其他3个傅氏系数：

(14)

(15)

(16)

式中：T表示抽汲周期；k表示2π周期内等分的份数，即离散化的采样点数；p表示从0到k各点序号。

以式(9)为边界条件，用分离变量法求解方程(1)，便可得出抽油杆任意深度x断面的位移随时间的变化。求解步骤如下：

首先令U(x，t)=X(x)T(t)，X(x)和T(t)分别为仅含x和t的函数，将其代入波动方程并整理可得：

(17)

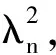
(18)

方程组(18)中第一个等式的周期解为：T(t)=einωt，代入方程组第一个等式可得方程(17)的特解λn：

λn=-αn+iβn

(19)

式(19)中αn与βn为实数，其值为

(20)

(21)

当n=0时，λ0=0，方程组(18)变为

(22)

其解为

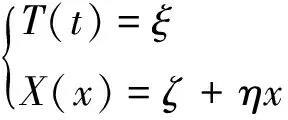
(23)

方程组(18)中第二个等式解为谐波方程：

X(x)=φnsinλnx+θncosλnx

(24)

综合以上各式，可求出方程式(17)的解为

(25)

经过变换可得到Gibbs方程的解析解为

(26)

由胡克定律，抽油杆柱任意深度x断面上的动载荷随时间的变化为

(27)

(28)

式(26)和(28)中的函数和系数如下：

On(x)=(knchβnx+δnshβnx)sinαnx+(μnchβnx+νnchβnx) cosαnx

(29)

Pn(x)=(knchβnx+δnchβnx) cosαnx+(μnchβnx+νnshβnx)sinαnx

(30)

(31)

(32)

(33)

(34)

根据U(x，t)与F(x，t)的解析式和x=L处边界条件，可得单级杆的泵功图。

粘滞阻尼系数公式由文献[4]给出：

(35)

上述论述适合于单级杆，对于多级杆情况，需要对抽油杆的载荷做分级计算。首先计算第一级杆末端载荷与位移；然后以第一级杆末端为第二级初始及边界条件，划分第二级抽油杆，再计算其末端载荷与位移。以此类推，直至求出最后一级末端的载荷与位移，得出最终的泵功图。根据力的连续性原理[5]，计算第二级杆载荷与位移所需的傅里叶系数与计算第一级杆系数的关系如下：

(36)

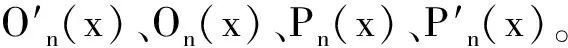
3 仿真分析

参考一实际油井进行其示功图与泵功图仿真，结果如图2泵功图的图形相对于示功图的图形发生了一定的扭曲，根据泵功图的形变故障分析，扭曲是由于抽油杆受到惯性力的作用产生的。

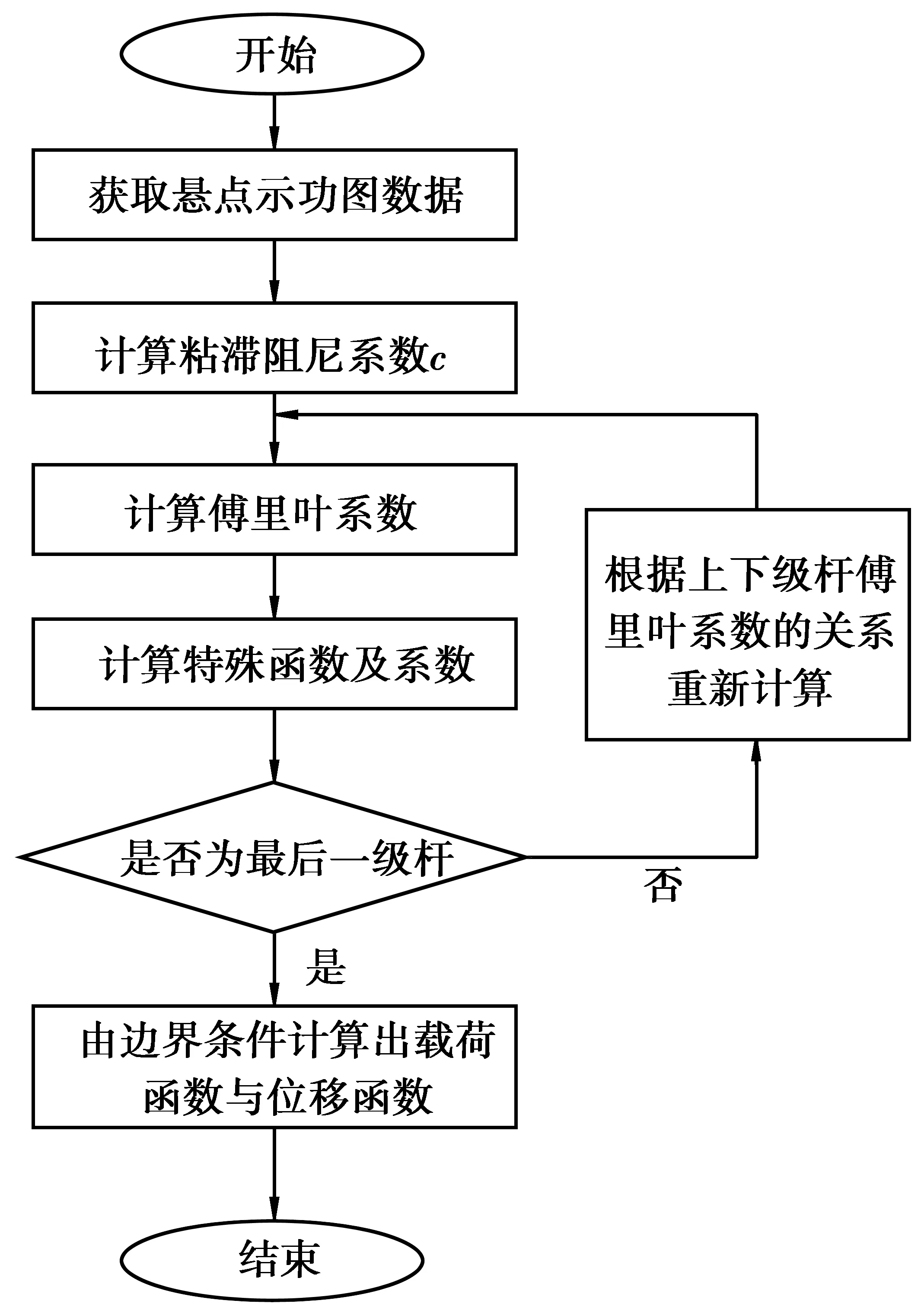
图1 计算泵功图流程

图2 油井的悬点示功图和泵功图

参考文献：

[1] 岳广韬.抽油机井地面示功图量油技术研究[D].中国石油大学，2011

[2] 董世民，崔晓华.计算抽油泵充满系数的新方法[J].石油机械，2002，30(1)：37-39

[3] 吴伟，陈国定，何焱，基于人工神经网络和灰度矩阵的泵功图诊断[J].西安石油大学学报：自然科学版，2007，22(3) ：14-17

[4] 张琪.基于泵功图分析的有杆泵井故障诊断系统[D]. 大连理工大学，2011

[5] 万仁博.采油工程手册[M].北京：石油工业出版社，2000