分数阶退化微分方程周期边值问题解的存在性*

王莉萍， 周宗福

(安徽大学 数学科学学院，合肥 230601)

0 引 言

近年来，各个科学领域中出现的问题越来越多地涉及分数阶微分方程，并且取得了许多成果[1-3].随着对诸如管理系统、生态系统、电力系统、工业工程系统等实际系统的研究，出现了大量的退化微分现象，引起了不少学者的关注，并取得了一些较为重要的结果[4-10].但对分数阶退化系统的研究还不多见.

文献[4]给出了分数阶退化微分方程Ex(α)(t)=Ax(t)+f(t)通解表达式.在文献[4]的基础上，进一步研究分数阶一般退化微分系统周期边值问题解的存在性.

研究如下形式的分数阶退化微分方程周期边值问题：

(1)

解的存在性，其中x(t)∈Rn为状态变量，E，A∈Rm×n(m≠n)，r(E)0，T>0是常数，x(α)(t)表示α阶Riemann-Liouville导数，且0<α<1.

1 预备知识

在后面的讨论中，需要下面的几个定义和引理.

定义1[4]对任何一方阵P∈Rn×n，如果存在方阵Pd∈Rn×n满足条件：

1) PPd=PdP；2) PdPPd=Pd；3) (In-PPd)Ph=0.

则称Pd为P的Drazin逆，其中h为某一非负整数，In为n阶单位阵，并称使条件3)成立的最小非负整数h为P指标，记为ind(P).

定义2[4]对于矩阵E，A∈Rm×n，假定A的列向量线性无关，定义EA=(YE)dY，其中Y∈Rn×m满足：

(Im-AY)(EY)d=0，YA=In

则称矩阵对(EA，Y)为矩阵对(E，A)的可解阵对，这里Im，In分别为m阶及n阶单位阵.

定义3[4]设f(t)∈C([0，∞)，R)，∀α∈R+，称

为α阶Riemann-Liouville分数积分.

定义4[4]设f(t)∈C([0，∞)，R)，∀α∈(0，1)，称

为α阶Riemann-Liouville分数导数，为方便，把Dαf(t)记为f(α)(t).

引理1[4]对于系统

Ex(α)(t)=Ax(t)+f(t)，t>0

(2)

E，A∈Rm×n(m≠n)，0<α<1.设(EA，Y)为(E，A)的可解阵对，ind(YE)=1，若f(t)是一阶可微的，且(Im-AY)(EYf(α)(t)+Imf(t))=0，则系统(2)的通解

(3)

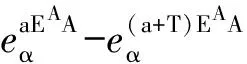
(4)

有唯一解

(5)

其中

证明由引理 1 即可证明.

引理3[5](Krasnoselskii不动点定理)

设K为Banach空间X中的一个有界闭凸集，映射F：K→K及G：K→K满足：

1) ∀u，v∈K，Fu+Gv∈K；

2) F为全连续的，G为压缩的.

则F+G在K上至少有一个不动点.

2 主要结果

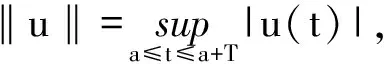
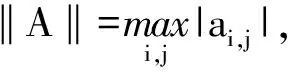
定理1 对于系统(1)，假设条件：

(A) ∀u1，u2∈Rn，∀t∈[0，∞)，‖f(t，u1)-f(t，u2)‖≤L‖u1-u2‖，L>0是常数，且pL<1；

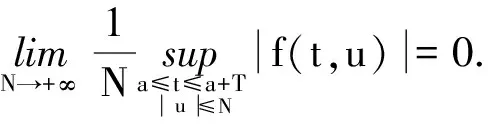
则周期边值问题(1)至少存在一个解.

证明对任意的u(t)∈CT，考虑周期边值问题

(6)

由引理 2 可知系统(6)有唯一解

(7)

其中

定义从CT到CT的算子F及G如下：∀u∈CT，有

则算子F+G的不动点就是系统(1)的解.

由条件(B)，则存在N1>0，使得

(8)

令K={u：u∈CT，‖u‖≤N1}，则K为E中的有界闭凸集.下面证明

1) ∀u，v∈K，Fu∈K，Gv∈K，Fu+Gv∈K；

2) F在K上全连续；

3) G在K上为压缩的.

1) ∀u，v∈K，证明Fu∈K，Gv∈K，Fu+Gv∈K，∀u，v∈K，

由式(8)可得

从而‖Fu+Gv‖≤N1，因此Fu+Gv∈K，由上述证明过程可以看出Fu∈K，Gv∈K.

2) 证明F在K上全连续. 即证 ① F在K上是连续的；② F在K上是紧的.

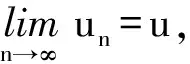
由于

② 证明F在K上是紧的，即证FK是列紧的.

由K的定义及FK⊂K知，K中的函数一致有界，所以FK中的函数也是一致有界的，下证FK是等度连续的.

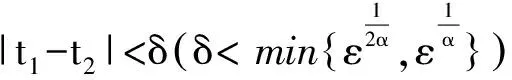
∀u∈K，有

可见FK是等度连续的，由Arzela-Ascoli定理可得，FK是列紧的，即得F在K上是紧的.综上所述，F在K上是全连续的.

3) 证明G在K上为压缩的.

∀u1，u2∈K，∀t∈[0，T]，由条件(B)可得

|Gu1(t)-Gu2(t)|=|(In-EAE)Y(f(t，u2(t))-f(t，u1(t)))|≤

‖(In-EAE)Y‖|f(t，u1(t))-f(t，u2(t))|

即‖Gu1-Gu2‖

综上所证，由引理 3 可得，F+G在K上至少有一个不动点u*，u*即为系统(1)的解.证毕.

参考文献：

[1] AGARWAL R P，ZHOU Y，HE Y Y. Existence of Fractional Neutral Functional Differential Equations[J]. Comput Math Appl，2010，59(3)：1095-1100

[2] BAI Z B. On Positive Solutions of a Nonlocal Fractional Boundary Value Problem[J]. Nonlinear Anal，2010(72)：916-924

[3] CHEN F L，ZHOU Y. Attractivity of Fractional Functional Differential Equations[J]. Comput Math Appl，2011，62(3)：1359-1369

[4] 张海，赵小文，蒋威. 分数阶一般退化微分系统的通解[J].数学杂志，2011，31(1)：91-95

[5] 周宗福，郑祖庥. 非线性退化时滞系统的周期解[J]. 系统科学与数学，2003，23(1)：43-50

[6] 张志信，蒋威. 具有分布时滞的广义系统的周期解问题[J].工程数学学报，2012，29(5)：725-732

[7] 蒋威. 退化时滞微分系统的通解[J]. 数学学报，1999，42(5)：770-780

[8] BONILLA B，RIVERO M，TRUJILLO J J. On Systems of Linear Fractional Diffrential Equations with Constant Coffients[J]. Appl Math Comput，2007，187(1)：68-78

[9] ZHOU X F，WEI J，HU L G. Controllability of a Fractional Linear Time-invariant Neutral Dynamical System[J]. Appl Math Lett，2013(26)：418-424

[10] FU X. Controllability of Neutral Functional Differential Systems in Abstract Space[J]. Appl Math Comput，2003(141)：281-296