几种概率分布高阶原点矩的计算*
姜 培 华
(安徽工程大学 数理学院,安徽 芜湖 241000)
正态分布又称高斯分布,是概率统计中最重要的分布之一,很多统计推断都是基于正态分布的假设,以标准正态分布为基石而构造的“三大抽样分布”在实际中有着广泛的应用,这三个概率分布不仅有明确的背景,而且其密度函数有明显的表达式.威布尔分布和对数正态分布是两种重要的寿命分布,威布尔分布在可靠性工程中被广泛应用,尤其适用于机电类产品的磨损累计失效的分布形式,被广泛应用于各种寿命试验的数据处理.对数正态分布常用于刻画绝缘材料的寿命和设备故障的维修时间.高阶矩是随机变量的重要数字特征,它在金融投资、保险和数据传输中都有着重要的应用,是求变异系数、偏度和峰度系数等其他特征的前提,更是参数估计和统计推断的基础,因此高阶矩的计算尤为重要.文献[1-7]重点研究了几类离散型分布的高阶原点矩的计算,如二项分布、负二项分布、泊松分布、几何分布和超几何分布等.此处考虑六类连续型分布(t分布、F分布、卡方分布、正态分布、威布尔分布、对数正态分布)的高阶原点矩的计算,并给出其精确的计算表达式.
1 预备知识及引理
定义1[8]称函数
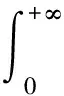
为伽玛函数,其中参数α>0.伽玛函数具有如下性质:
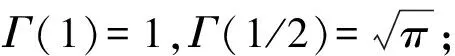
(2)Γ(α+1)=αΓ(α),当α∈N时,有Γ(n+1)=nΓ(n)=n!.
定义2[8]若随机变量X的密度函数为
则称X服从贝塔分布,记作X~Be(a,b),其中a>0,b>0都是形状参数.
定义3 若随机变量X具有密度函数
则称X服从三参数威布尔分布,记为X~W(μ,m,η),其中μ,m,η>0,分别为其位置、形状和尺度参数.
定义4[8]若随机变量X具有密度函数
则称X服从对数正态分布,记为X~LN(μ,σ2),其中μ,m,η>0,分别为其位置、形状和尺度参数.
引理1[9]若ξ~t(k),则η=ξ2~F(1,k),其中k为自然数.
引理2[10]若ξ~Be(a,b),则η=bξ/a(1-ξ)~F(2a,2b),其中2a,2b为自然数.
2 三大抽样分布与正态分布高阶矩的计算
随机变量高阶矩的计算本质上是分析学中的定积分问题,对于阶数较低密度函数简单的变量而言,计算其矩并不困难.在阶数较高,分布的密度函数较为复杂的情形下,若直接用定义法求解随机变量的高阶矩很困难,甚至无法实现.这时可以考虑概率分布之间的关系,将密度函数复杂的随机变量高阶矩的计算转化为密度函数简单的随机变量函数的高阶矩进行计算,这样可以起到化繁为简,同时也为高阶矩的计算提供一种新思路.
定理1 若随机变量T~t(k),则对r 其中,Γ(·)表示伽玛函数. 综上所述,定理1成立. 推论1 若随机变量T~t(k),则其期望和方差分别为 其中,Γ(·)表示伽玛函数. 故定理2成立. 推论2 若随机变量F~F(k,m),则其期望和方差分别为 证明在定理2中分别令r=1,2,再利用公式VarX=E(X2)-(EX)2即可得证. 证明由于X~χ2(n),又因自由度为n的卡方分布即为参数为(n/2,1/2)的伽玛分布,即Ga(n/2,1/2),从而可得 故结论成立. 定理4 若随机变量Y~N(μ,σ2),则对k∈N有 其中,E(Xr)为标准正态分布的r阶原点矩,并且 证明先求标准正态分布的高阶矩.由于N(0,1)的密度函数为偶函数,由对称性知,当r为奇数时E(Xr)=0;当r为偶数时, (r-1)E(Xr-2)=…=(r-1)(r-3)…3E(X2)=(r-1)(r-3)…3·1 再求N(μ,σ2)的高阶矩.对Y进行标准化,令X=(Y-μ)σ-1,则X=(Y-μ)σ-1~N(0,1),从而可得 其中 威布尔分布和对数正态分布是两种重要的寿命分布,威布尔分布在可靠性工程中被广泛应用,尤其适用于机电类产品的磨损累计失效的分布形式,被广泛应用于各种寿命试验的数据处理.对数正态分布常用于刻画绝缘材料的寿命、设备故障的维修时间和家庭中两个孩子的年龄之差. 定理5 设X服从参数为(μ,m,η)的三参数威布尔分布,则对k∈N有 其中,Γ(·)表示伽玛函数. 证明因X~W(μ,m,η),由定义3的密度函数可知 注1) 在W(μ,m,η)分布中,若取m=1,则可得双参数指数分布Exp(μ,η)的高阶原点矩的计算公式; 2) 在W(μ,m,η)分布中,若取m=1,μ=0,则可得指数分布Exp(η)的高阶原点矩的计算公式; 3) 在W(μ,m,η)分布中,若取m=2,μ=0,则可得瑞利分布高阶原点矩的计算公式. 推论3 若随机变量X~W(μ,m,η),则其期望和方差分别为 证明因X~LN(μ,σ2),由定义4的密度函数可知 推论4 若随机变量X~LN(μ,σ2),则其期望和方差分别为 综上,运用概率分布之间的关系,借助已有分布高阶矩的结果,可以将密度函数复杂的随机变量高阶矩的计算转化为密度函数简单的随机变量函数的高阶矩计算,这样就使得积分化繁为简,化难为易,开阔了思路.在“概率论”专业课程的教学中,任课教师在讲到相关内容时可以启发学生联想、对比和分析以前所学的概率分布,引导学生多学善思去寻求解法的创新,这样有助于学生加深对概率论统计知识的掌握和理解,从而激发学生的创造力和学习兴趣. 参考文献: [1] 杨青,陈光曙. 关于二项分布、Poisson分布和几何分布高阶的递推公式[J]. 大学数学,2009,25(4):103-108 [2] 王新利,陈光曙. 几何分布与负二项分布高阶的递推公式[J]. 高等数学研究,2011,14(2):15-16 [3] 朱振广,张志文. 求解Poisson分布和二项分布高阶的代数方法[J]. 辽宁工学院学报,2005,25(1):68-70 [4] 魏孝章. 关于几何分布的高阶原点矩的探讨[J]. 数学通报,2006,45(8):61-62 [5] 徐晓岭,费鹤良,王蓉华. 几何分布的两个特征[J]. 应用概率统计,2006,22(1):10-20 [6] 于晶贤,李金秋. 泊松分布高阶原点矩的两种计算方法[J]. 数学的实践与认识,2010,40(21):221-224 [7] 于晶贤.一类离散型随机变量高阶原点矩的递推计算方法[J]. 科学技术与工程,2010,15(15):3681-3683 [8] 茆诗松,程依明,濮晓龙.概率论与数理统计教程[M]. 2版.北京:高等教育出版社,2011 [9] 郑明,陈子毅,汪嘉冈.数理统计讲义[M]. 上海:复旦大学出版社,2005 [10] 茆诗松.贝叶斯统计[M]. 北京:中国统计出版社,1999

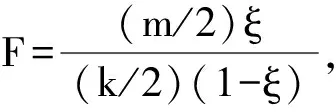
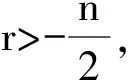
3 两大寿命分布高阶矩的计算
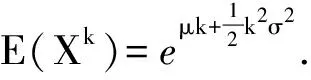
4 结束语

