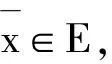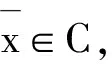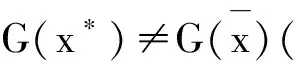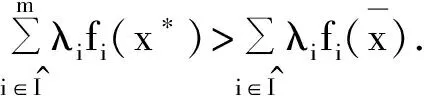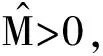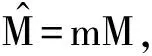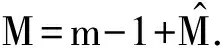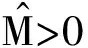向量优化问题恰当有效解的几个性质*
肖 浩, 黄龙光
(集美大学 理学院,福建 厦门 361021)
众所周知,向量优化的理论与方法已经在经济、金融、计算机、最优决策等许多领域扮演了十分重要的角色.自从1879年,意大利经济学家维弗雷多·帕雷托提出Pareto有效解这一概念以来[1],已经有越来越多的学者开始研究向量优化问题有效解的概念、性质.随着进一步的研究,恰当有效解的概念被提出来,其中ε-有效解的研究也取得了一些成果[2-4].近年来,Y.Jiang和S.deng在恰当有效解的基础上提出了α-恰当有效解[5].并讨论了有效解、恰当有效解和α-恰当有效解之间的关系.此处在文献[5-6]的基础上进步一讨论恰当有效解的相关性质,将目标函数引入参数变成更为一般的情形,通过对参数的控制讨论其有效解的存在情况.
1 预备知识
考虑如下向量优化问题:
(P) minF(x) s.t.x∈C
其中C⊂X是赋范线性空间X中的非空闭集,F(x)=(f1(x),…,fm(x))是一个从X到Rm的连续向量函数,其中Rm为m维欧几里德空间.
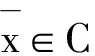
∀x∈C]⟹
用‖·‖1和‖·‖∞表示Rm中的l1-范数和l∞-范数[7].设y=(y1,…,ym)T∈Rm,有
[v]+=([v1]+,…,[vm]+)T
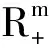
2 恰当有效解的性质
对于(P),定义
其中λ=(λ1,…,λm)T∈Rm是一个从X到Rm的连续向量函数,且λi>0.
类似于文献[8],有下面的定理.
定理1 对于(P),E是非空的当且仅当存在q∈C,使得最优化问题
证明⟹令y∈E,考虑下面优化问题
如果y不是其有效解,则存在一个z∈C,使得
f(z) 这与y∈E矛盾. ⟸ 假设对于y是(φ(q)),q∈C的有效解,但y∉E,则存在z∈C,使得 这与y是(φ(q)),q∈C的有效解矛盾. 注2 若x*是(P)的有效解,则它不一定是(P)的恰当有效解. 例1 令C={(x1,x2)|(x1-1)2+(x2-1)2≤1},F(x)=(x1,x2),则(1,0)和(0,1)在E内,但它们不是(P)的恰当有效解. (1) 现在介绍一种增强的恰当有效解,称之为α-恰当有效解. (2) 注3 式(2)中α=1时的情形即为定理2. 令G(x)=(λ1f1(x),…,λmfm(x))T∈Rm,则有以下定理成立. 定理3 对于(P),令x*∈E,则x*也是最小化问题f(x)+‖[G(x*)-G(x)]+‖1,x∈C的有效解. 注4 对于定理3,x*若是最小化问题f(x)+‖[G(x*)-G(x)]+‖1,x∈C的有效解,则它不一定是(P)的有效解. 例3 令m=1,f1(x)=x2,C=[0,∞),λ=1,则x*=1是x2+[1-x2],x∈C的有效解,但不是f1的有效解(它的有效解是0). 类似于问题(P),定义如下向量优化问题: (G) minG(x) s.t.x∈C 其中C⊂X是赋范线性空间X中的非空闭集,G(x)=(λ1f1(x),…,λmfm(x))∈Rm是一个从X到Rm的连续向量函数. (3) 的有效解. 证明⟹ 由于x*∈E,由定义3,知 其中式(4)是根据l1-范数和l∞-范数的关系得来,式(5)是根据α-有效解的定义得来. ⟸ 由于对任意的x∈C,x*都是式(2)的有效解,于是 即 若‖[G(x*)-G(x)]+‖∞=0,结论显然成立. 假设‖[G(x*)-G(x)]+‖∞>0,若j∈[1,k],使 ‖[G(x*)-G(x)]+‖∞=λj(fj(x*)-fj(x)) 则 ‖[G(x*)-G(x)]+‖∞=λj(fj(x*)-fj(x))≤ 类似于文献[9],有下面的推论. 参考文献: [1] YOUSHIKAZU S,HIROTAKA N,TETSUZO T. Theory of Multiobjective Optimization[M].New York:Academic Press Inc,1985 [2] LORIDAN. E-solutions in Vector Minimization Problems [J].Journal of Optimization Theory and Applications,1984,43(2):265-276 [3] 彭婕,赵克全. 向量优化问题ε-真有效解的一个性质 [J].重庆工商大学学报:自然学科版,2013,12(30):1-3 [4] RONG W D,WU Y N. E-weak Minimal Solutions of Vector Optimization Problems with Set-valued Maps [J].Journal of Optimization Theory and Applications,2000(3):569-579 [5] JIANG Y,DENG S. Enhanced Efficiency in Multi-objective Optimization [J].Journal of Optimization Theory and Applications,2013(2):201-209 [6] ALEXANDE J. Optimization on Metric and Normed Spaces [M].Berlin:Springer,1998 [7] 胡毓达. 多目标规划有效性理论 [M].上海:上海科学技术出版社,1994 [8] DENG S. On Efficient Solutions in Vector Optimization [J].Journal of Optimization Theory and Applications,1998,96(1):201-209 [9] Huang X X,YANG X Q. On Characterizations of Proper Efficiency for Nonconvex Multi-ob jective Optimization [J].Journal of Global Optimization,2002,23(2):213-231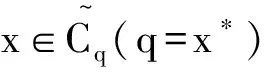
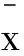
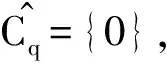
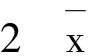
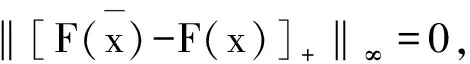
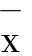
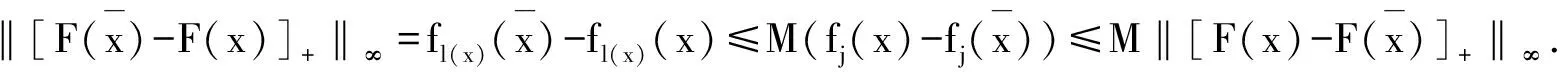
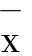
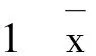
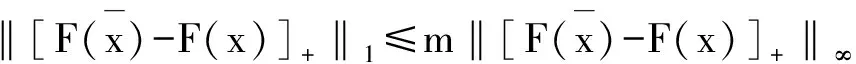
3 α-恰当有效解的性质