一类具有S型功能性反应系统的稳定性*

梁 娟， 尹礼寿， 刘岩岩

(1.太原工业学院 理学系，太原 030008；2.重庆大学 数学与统计学院，重庆 401331)

Holling型功能反应系统模型种类众多，研究这类模型具有及其重要的生物意义.这几年来，很多学者从不同侧面研究了Holling功能性反应函数的捕食-食饵模型[1-6].一般地，S型功能性反应函数的捕食-食饵系统可以表述为微分方程组[6]：

(1)

其中，x，y分别表示食饵和捕食者的种群密度，K表示食饵的进位容量，η>0表示捕食者的死亡率，r表示食饵的内在增长率，μ表示转化率，xP/(β+xP)表示功能反应函数，其中β表示半饱和常系数.系统(1)已有很多研究成果,文献[2]分析了一类具有HollingⅠ功能性反应模型的捕食者种群与食饵种群相互作用的数学模型，分别得到了至少有一个或者两个极限环的充分条件.当P=2时，系统(1)为Holling-Ⅲ类功能性反应模型，文献[3]对该系统给出了完整的定性分析，证明了该系统至多有一个极限环，并给出了存在极限环的充要条件.此处接着前人的研究成果，考虑当P=3时，系统(1)的动力性态.研究的模型为[6]

(2)

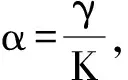
1 平衡点的动力性态

该节将研究式(2)的动力性态.在式(2)中，因为x，y分别表示食饵和捕食者的种群密度，因而只能在第一象限及其边界上讨论系统(2)的动力性态.容易知道，x轴的正半轴是式(2)的不变流形，而y轴的正半轴不是式(2)的不变流形.但是，经过y轴正半轴的轨线，都要进入到第一象限内.因而，第一象限及其边界是式(2)的不变集.下面将在第一象限及其边界上讨论式(2)的动力性态.

为了简化计算，先引入适当的非退化变换，将式(2)进行量纲变换T=(β+x3)t，转化为等价的系统

(3)

其中，m=μ-η，n=βη,若使得系统有正平衡点，需要保证m>0.

(4)

1) 当y=0时，系统有非负平衡点E1=(0，0)，E2=(b/a，0)；

注意到x0>0，y0>0，因此E3在第一象限内，当且仅当b>ac-1/3.

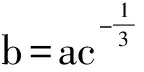
现在讨论式(3)在平衡点附近的动力性态.

定理1 平衡点E1是鞍点.

证明式(4)在平衡点E1处的Jacobi矩阵为

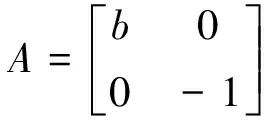
所以，特征方程为T(λ)=[λ-b][λ-(-1)],容易知道特征值为λ1=b，λ2=-1.因为式(3)所有参数都是正的，可以得到λ1>0，λ2<0.由文献[7]，可以得到E1为不稳定鞍点.证毕.

下面研究系统平衡点E2的动力性态.

定理2 关于平衡点E2，下列结论成立(其中c0=a3/b3)：

1) 当c>c0时，E2为不稳定鞍点；

2) 当c

3) 当c=c0时，E2是鞍结点.

证明式(3)在平衡点E2处的Jacobi矩阵为

所以，特征方程为T(λ)=[λ-(-b4/a3-b)][λ-(cb3/a3-1)].容易知道，特征值为λ1=-b4/a3-b，λ2=cb3/a3-1.因为式(3)所有参数都是正的，可以得到λ1<0.

由文献[7]，可以得到以下结论：

1) c>c0时，有λ2>0，则E2为不稳定鞍点；

2) c

3) c=c0时，有λ2=0，由E2的表达式知E2=(-b4/a3-b，0).

下面研究E2的动力性态.将平衡点E2移到原点，令x1=x-b/a，y1=y，做变换x2=x1+[ab/(a3+b3)]y1，y2=y1，则方程变为

(5)

其中，g=(a3b2-3a3b-2b5)/(a3+b3)2.由文献[7，8]知(b/a，0)为式(5)的鞍-结点，即当c=c0时，平衡点E2为式(3)的鞍-结点.

1) 当0b0时，E3为不稳定的结点或焦点；

3) 当0

证明容易知道，在定理3的条件下，E3是式(3)在第一象限内的平衡点.式(4)在E3处的Jacobi矩阵为

用|A|和tr(A)分别表示矩阵A的行列式和迹.令λ1，λ2表示矩阵的特征值，则

因为E3是正平衡点，因而|A(b)|>0，由文献[7，9]得到：

1) 当b>b0时，显然tr(A(b))>0，因为|A(b)|>0，所以Re(λ1)>0，Re(λ2)>0，则E2为不稳定的结点或焦点；

2 Hopf分岔及其稳定性

在定理3的3)中，当0

定理4 当m>1，b=b0时，式(4)在平衡点E3附近会发生Hopf分岔,并会在E3附近出现唯一的稳定极限环.

在式(3)中，将E3移到原点，引入变量变换x=x0+ζ1，y=y0+ζ2，并作Taylor多项式展开，得到式(6)

(6)

将式(6)写成下面的形式(式(7))：

(7)

选取两个复向量q=(1，-iwm)T，p=(1/2，-i/2wm)T，计算可以得到Aq=iwq和ATp=-iwp，并且〈p，q〉=1.由B和C的定义又得到

直接计算得到第一Lyapunov系数为

由文献[8，10]知，当l1(b0)≠0，式(3)会发生Hopf分岔.由结论知，l1(b0)<0时，式(3)会出现一个稳定的极限环.证毕.

参考文献：

[1] WANG Y Q.MA J Y.Qualitative Analysis on a Class of Predator—prey Model with Holling III Functional Response[J].Journal of Biomathematics，2004，19(4)：395-402

[2] 李林，吴晓非. 一类捕食-食饵系统的定性分析[J]. 生物数学学报，1993，8(1)：74-82

[3] 陈柳娟，孙建华. 一类Holling功能性反应模型极限环的唯一性[J].数学学报，2002，45(2)：383-388

[4] HSU S B，HUANG T W. Global Stability for a Class of Predator-prey System [J]. SIAM Journal on Applied Mathematics，1995，35(3)：763-783

[5] 王倩倩，李宝麟.一类具有功能性反应的捕食者一食饵系统的定性分析 [J].重庆工商大学学报：自然科学版，2012，29(2)：5-9

[6] 陈兰荪，孟新柱，焦建军. 生物动力学[M]. 北京：科学出版社，2009

[7] 张芷芬，丁同仁，黄文灶，等. 微分方程定性理论[M]. 北京：科学出版社，1985

[8] LAWRENCE P. Differential Equation and Dynamical Systems [M].New York：Spinger，1996

[9] PERKO L.Differential Equation and Dynamical System [M ]. 2nd ed. New York：Spinger，1996

[10] YURI A K. Elements of Applied Bifurcation Theory[M]. 2nd ed. New York：Spinger，2009