湖南省杉木与马尾松不同起源下生长率模型1)

陈丽聪 邓华锋 黄国胜 程志楚

(省部共建森林培育与保护教育部重点实验室(北京林业大学)，北京，100083) (国家林业局调查规划设计院)

森林永续利用的一项重要措施就是实行限额采伐管理，而准确预测森林生长量是确定森林采伐限额的重要依据［1］。材积生长率模型是预测森林生长量的重要手段，材积生长率模型中常用的自变量为年龄和胸径［2－5］。曾小波［6］在 2000 年，利用 53株平均木解析木研究了闽东杉木人工林材积生长率;廖志云等［7］在2006年，利用西藏493个样地，建立西藏自治区主要树种的生长率模型。本研究利用湖南省第六次、第七次森林清查数据中杉木与马尾松的所有调查数据，建立不同起源下的生长率模型并进行对比分析。

1 数据来源与整理

湖南省在1999年、2004年分别进行第六次、第七次森林资源连续清查，本文利用两次清查数据，从中选出杉木(Cunninghamia lanceolata)与马尾松(Pinus massoniana)所有单木资料，其中杉木单木总株数为42 612株、人工杉木25 166株、天然杉木11 126株;马尾松单木总株数为21580株、人工马尾松5 921株、天然马尾松15 137株。

对两期数据进行连接处理，整合到一起。其中，样木材积是根据一元材积模型，通过单木胸径求算得来，根据前后两期单木胸径，求出两期胸径的平均值作为自变量，然后按照普雷斯勒公式计算。

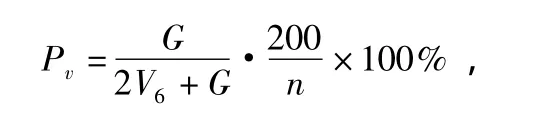
计算出1999年到2004年5 a期间杉木与马尾松的材积生长率作为因变量，公式如下:

式中:G表示材积生长量，V7、V6分别表示第七次、第六次清查数据中的材积值，n表示间隔时间(5 a)，Pv表示材积生长率。

理论上讲，随着林木年龄的增长，胸径会越来越大，而生长率也存在一个先上升，到达某一个顶峰之后，生长率开始随着胸径的变大而减小，当胸径的生长量等于或小于测量误差时，所测得的生长量可能为0或负值，这些都是正常发生的，不能随便剔除，而且由于数据量过大，如果是用3倍标准差的方法来剔除数据，很容易将正常的单木资料剔除，故本研究在整理阶段，不剔除任何数据，只在后期建模阶段，结合散点图与原始数据，剔除明显离散点。

整理结果发现，人工杉木两期平均胸径最小为5.15 cm，最大为41.25 cm，生长率最小为0.189 6%，最大为38.2456%;天然杉木两期平均胸径最小为5.15 cm，最大为39 cm，生长率最小为0.213 9%，最大为39.583 6%;人工马尾松两期平均胸径最小为5.05 cm，最大为 52 cm，生长率最小为 0.155 2，最大为36.039 6;天然马尾松两期平均胸径最小为5.05 cm，最大为74.4 cm，生长率最小为0.032 2%，最大为 38.122 1%。

2 结果与分析

由于森林资源清查数据的样木资料中只有胸径一个关键因子，没有树高与林龄，故选择的参考模型中应只有胸径一个自变量。徐雁南、周春国［5］在1996年关于单木生长率模型的研究中提到一个自变量只有胸径，且回归剩余标准差较小，能良好反应树木生长的模型。模型公式为:

P=a+b·D+c/D2+d·lnD。

其中:D 为胸径，a，b，c，d 为参数。

模型的建立分为建模和检验两部分，其中随即选取数据中的80%用于建模，剩余20%的数据用于模型的检验。用于检验的指标主要有决定系数R2、均方根误差、总相对误差及真实值与预测值线性关系的决定系数R21。具体公式见表1。

表1 模型检验评价指标

2.1 杉木生长率模型的建立

湖南省第六次、第七次森林资源连续清查都存在的保留木中，杉木单木共36 292株，其中包括人工杉木25 166株，天然杉木11 126株。由于数据量过大，散点图过于密集，故将数据进行0.5 cm的径阶分组处理。

2.1.1 人工杉木生长率模型

将25 166株人工杉木按80%与20%的数据比例分成两部分，其中20 242株用于建模，4 924株用于检验，建模数据的胸径范围为5.15～38.55 cm，生长率范围为0.19% ～38.24%;检验数据胸径范围为5.20 ～41.25 cm，生长率范围为0.19% ～36.80%，按0.5 cm径阶处理之后部分数据见表2。径阶整理后的散点图如图1。由图1可以看出存在部分离散点，然后利用径阶处理之后的数据结合原数据，剔除4个异样原数据，建模总数为20 238株，剔除离散点之后，重新按0.5 cm径阶处理，处理结果如图2。

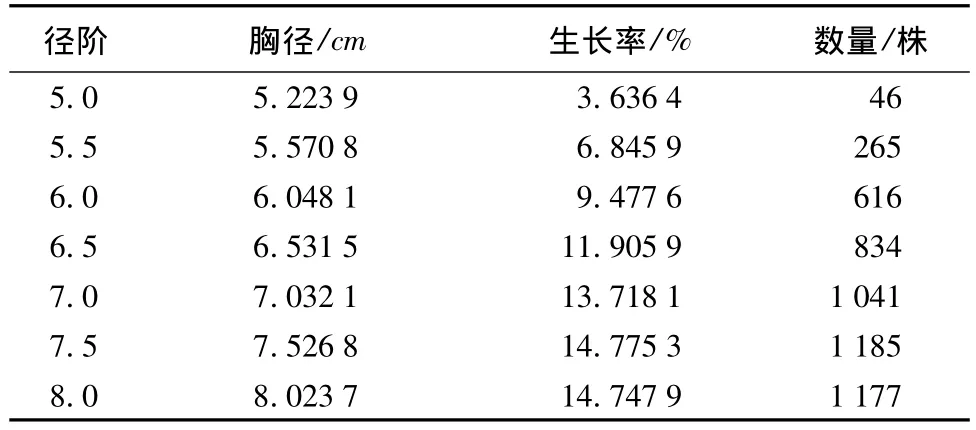
表2 径阶处理后的人工杉木数据

图1 径阶整化后的人工杉木生长率散点图

图2 剔除离散点后人工杉木生长率散点图

根据生长率模型进行模型拟合，拟合结果如图3，决定系数R2=0.950生长率模型结果为P=79.024+0.616D －916.025/D2－26.692lnD。

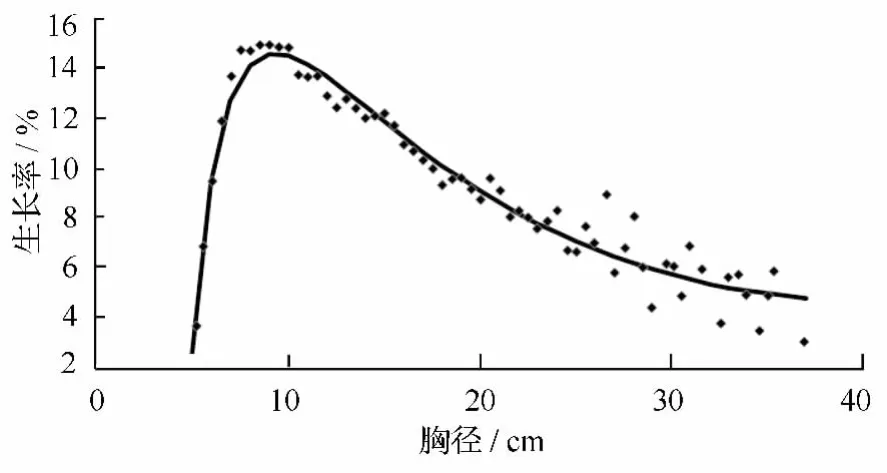
图3 人工杉木生长率拟合效果图

用剩余20%数据进行检验，检验结果显示，模型的决定系数为0.95，总相对误差为0.39%，预估精度为95.73%，实测值与预测值线性关系的决定系数为0.82，残差分布图见图4。

由检验结果可以看出，人工杉木生长率模型的拟合精度到达95%以上，模型的建模效果跟检验效果都较好，残差分布无明显异质性，绝大多数残差点都落在±2倍标准差之间，模型适用性强。

图4 人工杉木生长率模型检验数据残差分析

2.1.2 天然杉木生长率模型

湖南天然杉木单木总株数总计11 126株，其中8 915株用来建模，2 211株用来检验，建模数据的胸径范围为5.15～34.80 cm，生长率范围为0.21% ～39.56%;检验数据胸径范围为 5.20 ～39.00 cm，生长率范围为0.25% ～35.29%，按0.5 cm 径阶处理之后，部分数据见表3。

表3 径阶处理后的杉木天然林数据

径阶处理后的散点图见图5，与人工杉木的处理情况类似，根据原数据与散点图的离散情况，剔除2个异样原数据，建模总数为8 913株，然后按0.5 cm径阶重新整理，散点图结果如图6。

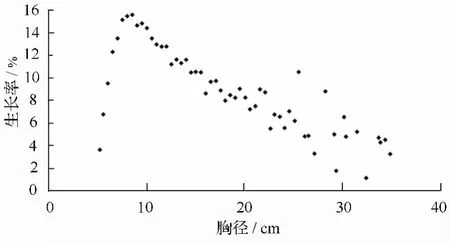
图5 径阶整化后的天然杉木生长率散点图

图6 剔除离散点后天然杉木生长率散点图

根据生长率模型进行模型拟合，拟合结果如图7，决定系数R2=0.92生长率模型结果为P=93.264+0.901D －1 031.942/D2－33.707lnD。

图7 天然杉木生长率拟合效果图

用剩余20%数据进行检验，检验结果显示，模型的决定系数为0.92，总相对误差为1.13%，预估精度为93.24%，实测值与预测值线性关系的决定系数为0.86，残差分布图见图8。

图8 天然杉木生长率模型检验数据残差分析

由检验结果看出，天然杉木生长率模型的拟合精度达到93%以上，总相对误差较小，建模效果与检验效果都较理想，残差分布无明显异质性，绝大多数残差点都落在±2倍标准差之间，模型适用性强。

2.2 马尾松生长率模型的建立

湖南省第六次、第七次森林资源连续清查都存在的保留木中，马尾松单木共21 058株，其中包括人工马尾松5 921株，天然马尾松15 137株。数据处理方法与杉木一样，其中人工马尾松中4 756株用来建模，1 165株用来检验，建模数据的胸径范围为 5.05～50.15 cm，生长率范围为0.16% ～36.04%;检验数据胸径范围为 5.25 ～52.00 cm，生长率范围为0.32% ～34.62%;天然马尾松中12 178株用来建模，2 959株用来检验，建模数据的胸径范围 为5.05～74.40cm，生长率范围为0.03% ～38.12%;检验数据胸径范围为 5.05 ～44.05 cm，生长率范围为0.03% ～36.52%，将所有数据进行0.5 cm的径阶分组处理，处理之后的部分数据见表4、表5。

通过径阶处理之后的人工马尾松与天然马尾松的散点图见图9、图10。

表4 径阶处理后的人工马尾松数据

表5 径阶处理后的天然马尾松数据

图9 径阶处理后的人工马尾松生长率散点图

图10 径阶处理后的马尾松天然林生长率散点图

从散点图中可以明显可以看出存在异样点，结合原始数据与散点图，人工马尾松中剔除2个异样原数据，建模总数为4 754株，天然马尾松中剔除4个异样原数据，建模总数为12 174株，然后按0.5 cm径阶重新整理，散点图结果如图11、图12。

图11 剔除离散点后人工马尾松生长率散点图

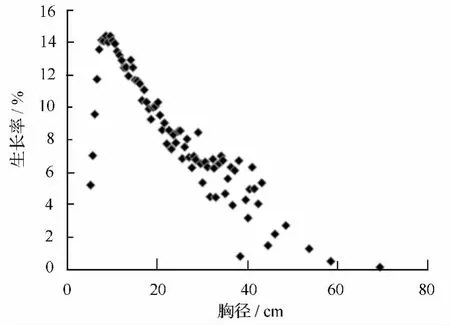
图12 剔除离散点后天然马尾松生长率散点图

以上两种类型的散点图均可看出一定规律，根据生长率模型进行模型拟合，拟合结果如图13、图 14。

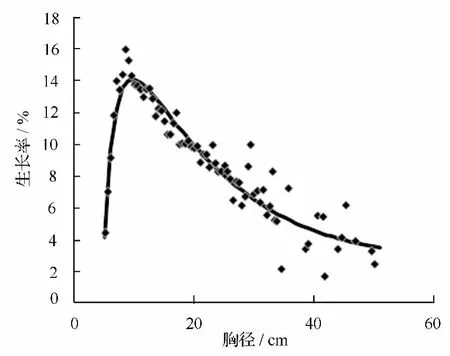
图13 人工马尾松生长率拟合效果图

人工马尾松模型的决定系数R2=0.905，生长率模型结果为 P=58.183+0.272D －685.983/D2－17.356lnD;天然马尾松模型的决定系数 R2=0.928，生长率模型结果为 P=50.582+0.143D －590.271/D2－14.059lnD用剩余的20%人工马尾松与20%天然马尾松进行上述模型的拟合检验，两种类型的各项检验指标结果显示，人工马尾松生长率模型的决定系数为0.91，总相对误差为1.69%，预估精度为94.45%，实测值与预测值线性关系的决定系数为0.74;天然马尾松生长率模型的决定系数为0.93，总相对误差为 0.62%，预估精度为 95.09%，实测值与预测值线性关系的决定系数为0.75，两种类型的残差分布图见图15、图16。

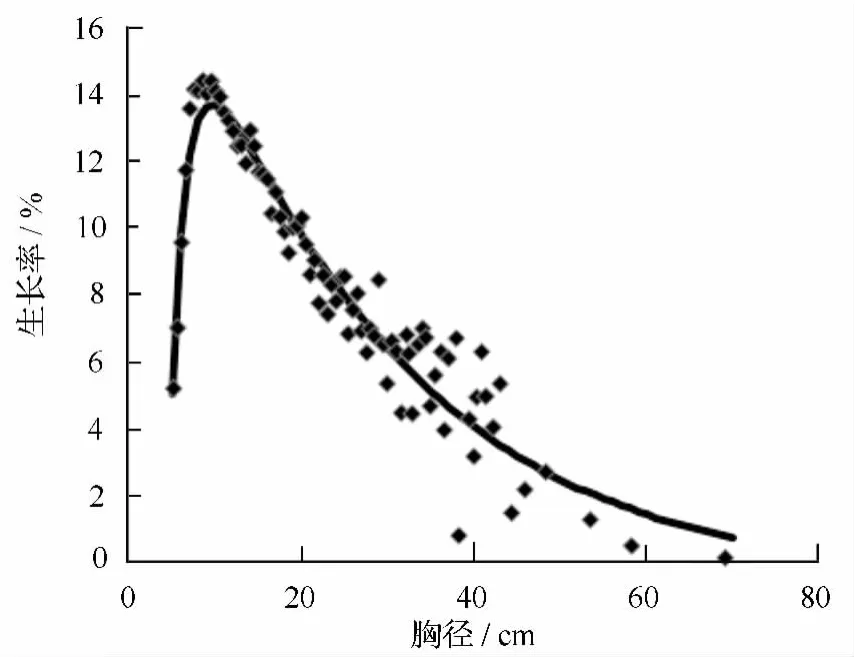
图14 天然马尾松生长率拟合效果图

图15 人工马尾松生长率模型检验数据残差分析

图16 天然马尾松生长率模型检验数据残差分析

由检验结果看出，人工马尾松与天然马尾松生长率模型的拟合预估精度都达到94%以上，总相对误差也较小，建模效果与检验效果都较理想，残差分布无明显异质性，绝大多数残差点都落在±2倍标准差之间，模型适用性强。

2.3 不同起源生长率模型的对比

将人工杉木与天然杉木、人工马尾松与天然马尾松拟合好的生长率模型进行分起源对比分析，对比结果见图17、图18。由图中可以看出，4种类型的生长率曲线趋势基本一样，人工杉木与天然杉木在胸径为11 cm左右时，生长率达到最大值，在胸径＞11 cm时，人工杉木与天然杉木生长率有一定差别;人工马尾松与天然马尾松在胸径为13 cm左右时，生长率达到最大值，整个数据范围内，生长率变化情况基本一致。

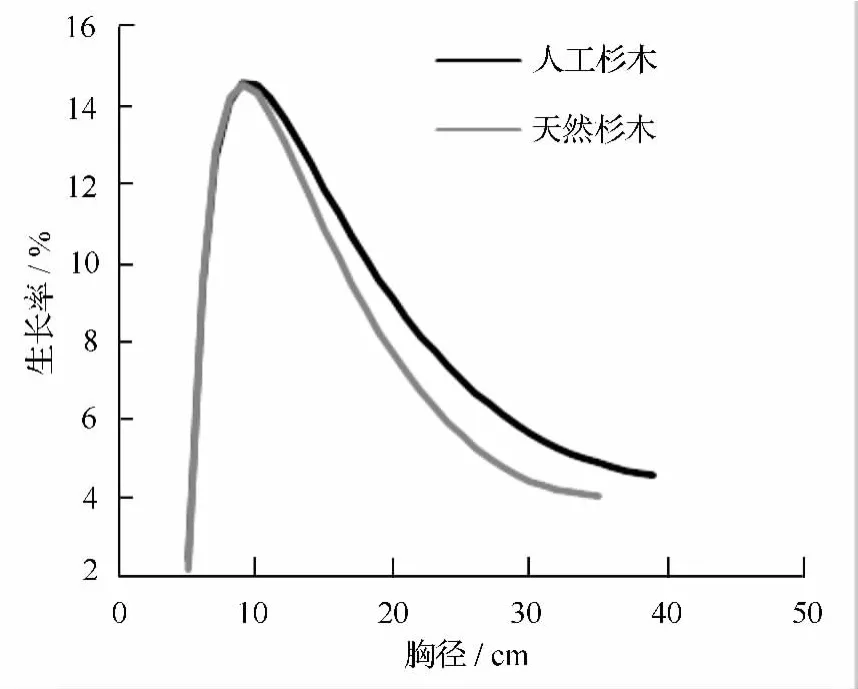
图17 不同起源杉木生长率模型对比

图18 不同起源马尾松生长率模型对比

3 结束语

从4种类型的建模结果来看，所建模型精度都在90%以上，建模与检验指标都在允许误差之内，所建模型符合要求［5］，而且本研究所用的研究数据来自全国森林资源连续清查，基本能反映全省情况，所建模型不仅可以用于研究数据范围内的推算，也可用于生长率预估。

由不同起源生长率对比结果可以来看，在胸径＜11 cm时，人工杉木与天然杉木的生长率变化情况基本一致，在胸径＞11 cm情况下，人工杉木的生长率比天然杉木的生长率下降更缓慢，即说明在胸径＞11 cm时，同一胸径下，人工杉木比天然杉木生长率高;在胸径＞35 cm时，同一胸径下，人工马尾松比天然马尾松生长率高，在胸径＞43 cm后，基本都为天然马尾松。在相同胸径条件下，对人工马尾松、天然马尾松生长率曲线对应的生长率进行差异性检验，结果显示，差异不显著，即人工马尾松与天然马尾松生长率变化情况差别不大。

［1］ 曾伟生.西藏天然云杉林兼容性材积生长率模型系统研究［J］.北京林业大学学报，2008，30(5):87 －90.

［2］ 程光明.杉木人工林材积生长率表编制的研究［J］.福建林业科技，2006，33(3):56 －59.

［3］ 曾伟生，骆期邦.二元材积生长率标准动态模型研究［J］.中南林业调查规划，1992(3):1－6.

［4］ 王树选，赵海林，聂爱社.刺槐林分生长率测算方法探讨［J］.林业资源管理，1987(5):45－50.

［5］ 徐雁南，周春国.单木生长率模型的研究［J］.林业资源管理，1996(4):23－25.

［6］ 曾小波.闽东杉木人工林材积生长率表的编制［J］.林业勘察设计，2002(2):10－13.

［7］ 廖志云，曾伟生.西藏自治区主要树种生长率模型的研建［J］.林业资源管理，2006(3):36－38.

［8］ 何庆斌，刘新建.林木材积生长率的研究［J］.林业勘察设计，1998(3):37－38.

［9］ 黄修麟.尤溪国有林场杉木人工林弹幕采集生长率表编制研究［J］.林业勘察设计，2010(2):8 －11.