基于自适应阈值的小波包在松动部件信噪分离中的研究
杨 波,夏 虹,张晓玉
(哈尔滨工程大学 核安全与仿真技术国防重点学科实验室,黑龙江 哈尔滨 150001)
松动部件是指反应堆内部件由于损坏、老化、腐蚀等原因而导致脱落的部件,在维修、换料、运行过程中进入主冷却剂系统。如果不能及时检测并排除松动部件,可能会增加传热管磨损和破裂、燃料包壳破损、控制棒卡棒等事故的风险。因此,在各国的反应堆主回路安全规范中规定,反应堆必须安装松动部件监测系统(LPMS)。松动部件监测系统主要有以下3个功能[1]:1) 实时监测松动部件冲击信号并根据设定的阈值触发报警;2) 对松动部件发生冲击的位置进行估计;3) 对松动部件的质量进行估计。从反应堆复杂的背景噪声中提取出冲击信号并对其相关特征进行详细分析是LPMS正常工作的前提。
反应堆系统中设备繁多,结构复杂,各种噪声以非线性的方式相互耦合在一起形成复杂的背景噪声。背景噪声由随机部分(如流动噪声)和确定部分(如依赖主泵转速的噪声)组成,是一种宽频带非高斯噪声。松动部件冲击产生的应力波到达各传感器的时间是定位研究的关键,松动部件质量估计通常是应用冲击信号在频域上的特征。小波包变换是一种信号的时频分析方法,具有多分辨分析的特点,在时-频域均能表征信号的局部细节,因此很适合用于信号的降噪处理和突变信号的识别[2]。反应堆在不同运行工况下背景噪声强度及频域特征均会不同,因此,本文提出一种自适应阈值选取的方法对含噪的松动部件冲击信号进行降噪处理。
1 自适应阈值的小波包去噪
1.1 小波包变换原理
小波包分析是20世纪90年代在小波分析的基础上发展而来的时-频分析方法。与小波分析相比,应用小波包的方法对信号分析会更加精细,对小波分析中没有分解的高频部分也进行了分解,并能根据被分析信号的特点,自适应地选择相应频带,使之与信号频谱相匹配,从而提高了时频分辨率。一棵3层小波包分解的完整树如图1所示。分解层数越多,小波包的尺度越大,小波包系数对应的空间分辨率越低。通过选择合适的分解层数及对不同的分辨率空间进行分析处理,以实现去噪目的。
⊕
其中:n为分解空间;j为分解层数;Z为整数。

(1)
(2)
其中,hk、gk分别为低通滤波器系数和高通滤波器系数,gk=(-1)kh1-k。
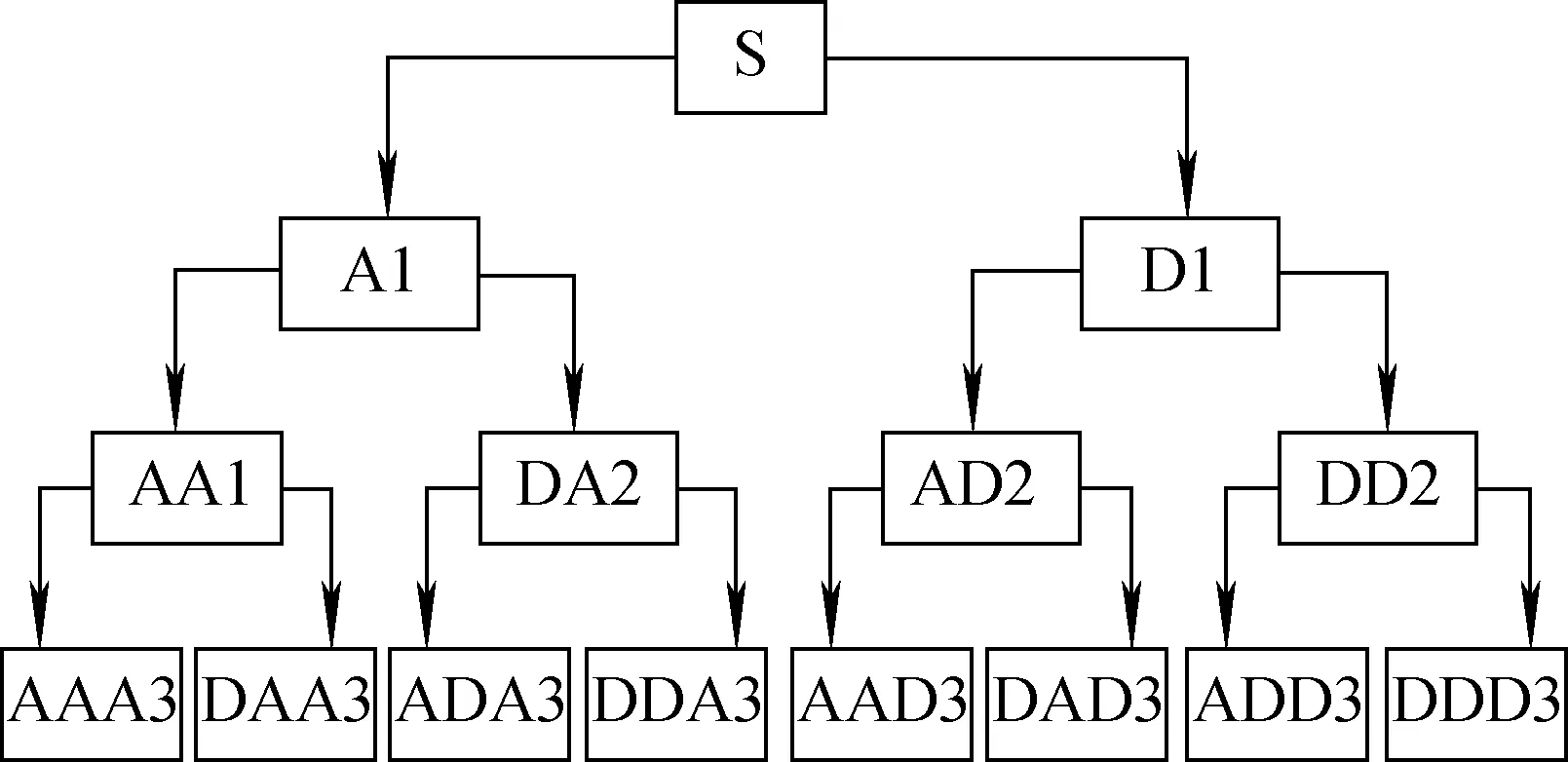
图1 3层小波包分解树
当n=0时,由式(1)、(2)得:
(3)
(4)
式(3)、(4)分别为尺度函数u0(x)与小波函数u1(x)的双尺度方程。利用式(1)得到以下空间分解:
⊕
(5)
根据以上推导,定义小波包:由式(1)~(4)构造的序列{un(x)}(其中n∈Z+,Z+为正整数)称为由基函数φ(x)=u0(x)确定的小波包。
(6)
(7)
其中,d为小波包分解系数。

(8)
1.2 自适应阈值选取
在选取去噪阈值方面,通常采用固定阈值、最小极大方差阈值、基于Stein无偏似然估计阈值及启发式阈值等。
典型的松动部件冲击信号与幅频谱及小波包分解如图2、3所示。实验发现松动部件冲击信号为一振荡衰减信号,持续时间约为200 ms。将冲击信号进行快速傅里叶变换(FFT)和3层小波包变换可发现冲击信号在很宽的频带上均有能量存在。

图2 松动部件冲击信号

图3 冲击信号在各尺度上的小波包系数
根据Parseval能量积分等式,设信号用x(t)表示,那么它在时域上的能量为:
(9)
其中,di(j,k)表示信号第j层分解上第k个子频带的第i个小波包系数[3]。
从式(9)可看出,可以用小波包系数来表征信号的能量。
背景噪声是一种宽频带的非高斯噪声,且随工况变化会发生变化。背景噪声经小波包分解后在各子频带上也有能量分布,因此需对每个子带上的小波包系数进行去噪处理,且阈值需跟踪各种工况变化。如果各子带阈值选取过大,会滤掉部分有用信号,如果各子带阈值选取过小,又达不到去噪的目的。因此,本文提出一种基于时间窗的自适应阈值选取。
假设在实际情况中,松动部件冲击事件为一小概率事件,在大部分的运行过程中不会发生,所采集到的信号大部分为正常信号和干扰信号。干扰信号通常为电气干扰(如电子干扰脉冲及过载)和机械干扰(如控制棒动作)[4]。电气干扰持续时间很短,机械干扰持续时间相对较长。
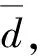
根据式(9),每个时间窗内的小波包平均能量为:
(10)

各时间窗的平均能量如图4所示。

图4 各时间窗的平均能量
经过这样处理,采集到的每次信号通过小波包分解后,每个子频带均可根据自适应的方法找出噪声分量,确定每一噪声分量的小波包系数阈值λj。
1.3 阈值处理函数
小波包去噪的思想就是将分解的小波包系数与选定的阈值进行比较,将小于阈值的小波包系数置零,将大于阈值的系数通过一定的阈值函数进行处理。目前通常使用的阈值函数是硬阈值函数与软阈值函数。硬阈值函数是一种直接保留的方式,但系数在λ和-λ处不连续;软阈值函数是将系数按一固定向量向零收缩,虽然软阈值函数在上述两点连续,但由于存在一恒定偏差,会影响系数的重构。为了克服这两种方法的缺点,文献[6]构造了一种新阈值函数:
(11)
新阈值函数示意图如图5所示。

图5 不同的阈值函数
从图5可看出,当系数的绝对值增大时,新阈值函数系数的估计值会趋于硬阈值函数,从而避免了出现一个固定向量的缩减。上述阈值函数中,N是一可改变的常数:当N不断减小时,新阈值函数趋近于硬阈值函数;当N不断增大时,新阈值函数会趋近于软阈值函数。
2 实验与分析
2.1 实验装置设计
为了模拟松动部件撞击一回路压力边界时产生的冲击加速度信号,并采集此信号用作后续分析,设计了钢球冲击实验装置(图6)。该装置由直径1 m、厚度10 mm的钢板,压电式加速度传感器,数据采集卡,放大器及电脑等组成。用不同质量的钢球模拟松动部件,从不同高度自由落体冲击钢板。模拟冲击信号与实际信号存在一些差异,主要是信号频率分布的差异,且实际电厂环境中一回路充满水,这使得信号低频成分比例增大[7]。
为了选取合适的传感器、放大器型号和布置传感器的安装位置,采用ANSYS LS-DYNA非线性动力学分析软件对实验装置模态和冲击过程进行仿真模拟。为尽量避免实验装置本身对测量结果的影响,传感器探测点选择模态影响最小的点,通过LS-DYNA计算,将传感器布置在钢板中心处。

图6 钢球冲击实验装置
2.2 数据采集与分析

图7 仿真噪声信号
在电厂中,加速度传感器采集到的信号是松动部件冲击与背景噪声的混合信号。根据相关文献对实际噪声的描述[8],可知实际噪声是一种宽频带的有色噪声。因此,在MATLAB中,通过设计不同的滤波器对白噪声进行滤波、叠加,得到了有色噪声的仿真信号,如图7所示。
将数据采集卡的采样频率设置为50 kHz,采样时间为1 s,采集到的冲击信号如图2所示。将采集到的信号以一定信噪比混入仿真噪声,如图8所示。

图8 信噪比为30 dB的松动部件冲击信号
对混入噪声的信号进行4层小波包分解,再用上述方法对分解系数进行处理。经过大量的实验发现,阈值函数的常数N取值应在0.6~1.2之间:如果过大,去噪效果不佳;如果过小,信噪比不但没有增加,反而降低。处理后得到的重构信号如图9所示。
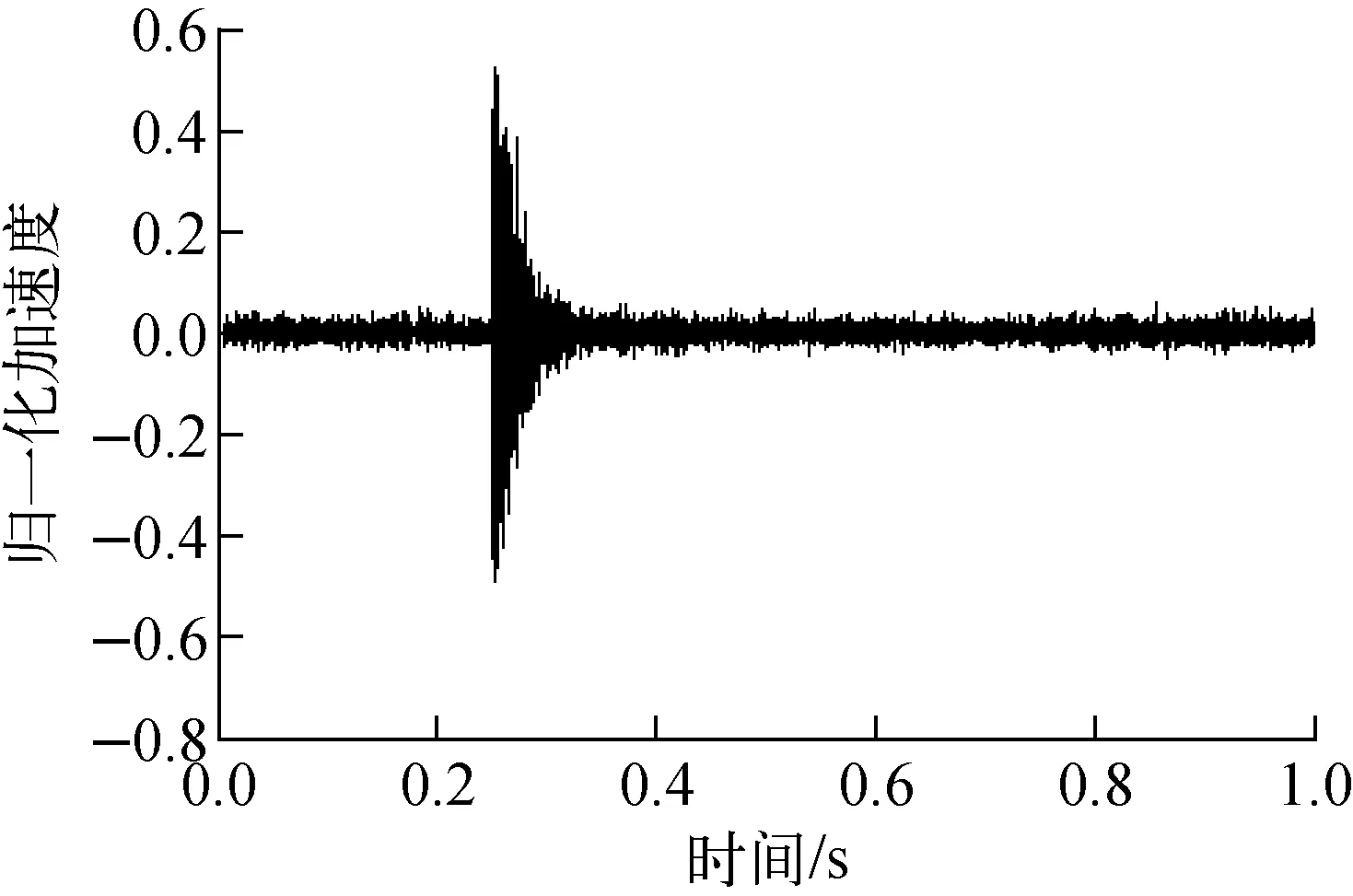
图9 去噪后的信号
为进一步检验去噪效果,将去噪前与去噪后的幅频谱进行对比,如图10所示。
由图10可看出,在信噪比为30 dB的情况下,本文提出的方法能较好去噪,提高了信噪比。
经过测试,当信噪比进一步降低(如20 dB),这种方法在时域上也能有效抑制部分噪声,但频域上几乎已得不到冲击信号的频率特征。当信噪比进一步降低,冲击信号被噪声完全淹没时,这种去噪方法会失效。
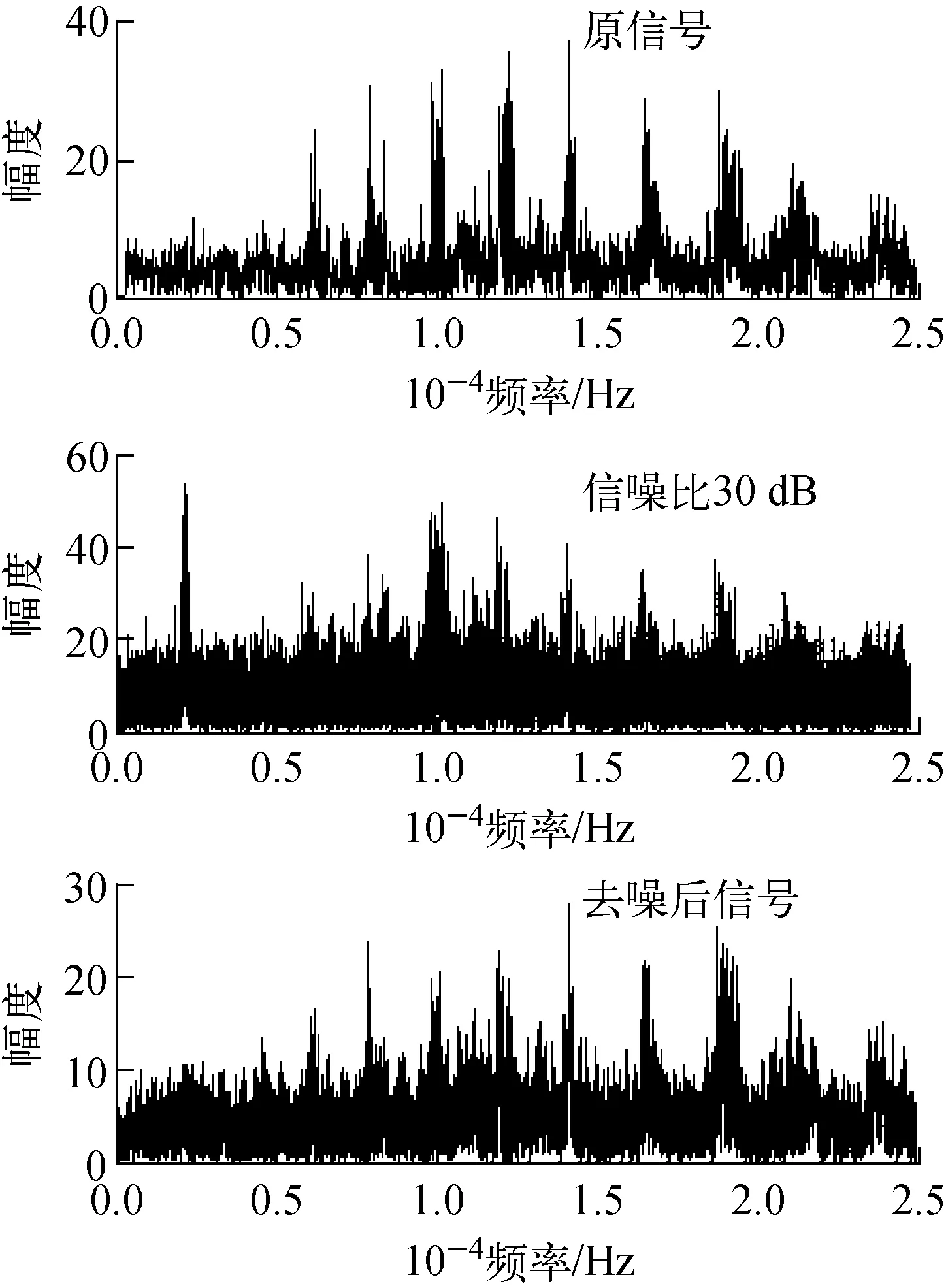
图10 去噪效果对比
为验证这种方法的自适应效果,本文进行了一个仿真实验。将1个35 g钢球在70 cm处下落的冲击信号加入噪声,信噪比为30 dB;将1个395 g钢球在130 cm处下落的冲击信号也加入噪声,信噪比为22 dB。将两个混有噪声的信号拼接在一起,如图11所示。
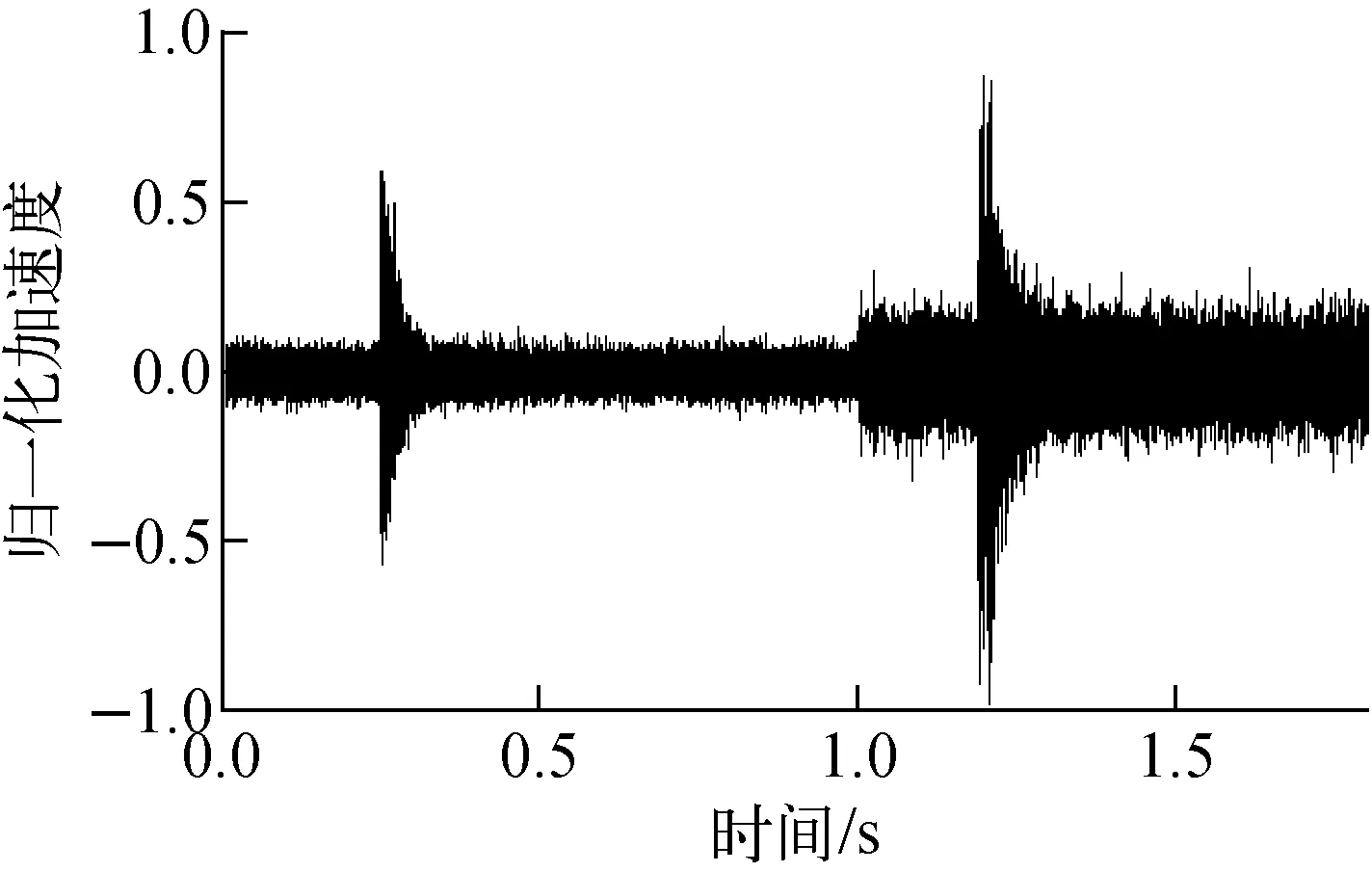
图11 不同信噪比的混合信号
由图11可知,整个过程信噪比并不相同,如果采用传统的全局阈值,去噪效果势必不理想。本文提出的自适应方法在每一分析阶段的每层均能得到一个阈值,这一段的去噪分析也是基于这个阈值进行的。去噪后的重构信号如图12所示。

图12 去噪后的混合信号
3 结论
将混入噪声的信号用小波包进行分解,然后基于能量自适应选择阈值,用阈值函数对小波包分解系数进行处理,最后将处理后的系数进行重构得到重构信号。通过对重构信号的分析,得到如下结论。
1) 在一定信噪比下,本文提出的方法能有效滤掉非高斯背景噪声。在信噪比较低的情况下,能抑制部分噪声,能准确识别冲击信号。但不能得到较清晰的频率分布。
2) 与其他时频分析方法相比,本文提出的方法能跟踪设备运行状态变化时背景噪声的变化,采用加时间窗的方式自适应确定背景噪声的阈值,不需要过多的先验知识。
3) 采用了一种新阈值函数,克服了传统阈值函数的弱点,且可通过调整常数来调整阈值函数,使得阈值函数的使用更加灵活。
参考文献:
[1] 赵翼瑜. 压水堆核电厂松动部件监测[J]. 核动力工程,1989,10(2):93-96.
[2] 陈志辉,夏虹,邬芝胜,等. 小波变换在突变信号识别中的应用[J]. 核动力工程,2013,34(2):62-67.
CHEN Zhihui, XIA Hong, WU Zhisheng, et al. Application of wavelet analysis in signal singularity detection[J]. Nuclear Power Engineering, 2013, 34(2): 62-67(in Chinese).
[3] 贺银芝,沈松,应怀樵,等. 小波包分解及其能量谱在发动机连杆轴承故障诊断中的应用[J]. 振动工程学报,2001,14(1):72-75.
HE Yinzhi, SHEN Song, YING Huaiqiao, et al. Application of wavelet packet decomposition and its energy spectrum on the fault diagnosis of reciprocation machinery[J]. Journal of Vibration Engineering, 2001, 14(1): 72-75(in Chinese).
[4] 陈忻,刘芳,王季能. 核电厂松动部件监测系统误报警分析处理与改进建议[J]. 核科学与工程,2012,32(增刊1):57-62.
CHEN Xin, LIU Fang, WANG Jineng. The analysis and improvement suggestion for the false alarm from nuclear power plant loose components monitoring system[J]. Nuclear Science and Engineering, 2012, 32(Suppl. 1): 57-62(in Chinese).
[5] 李翰芳. 一种新的非高斯分布噪声下的小波去噪[J]. 湖北工业大学学报,2011,26(2):136-139.
LI Hanfang. A new wavelet de-noising method under non-Gaussian distribution[J]. Journal of Hubei University of Technology, 2011, 26(2): 136-139(in Chinese).
[6] 张维强,宋国乡. 基于一种新的阈值函数的小波域信号去噪[J]. 西安电子科技大学学报:自然科学版,2004,31(2):296-299.
ZHANG Weiqiang, SONG Guoxiang. Signal de-noising in wavelet domain based on a new kind of thresholding function[J]. Journal of Xidian University: Natural Science Edition, 2004, 31(2): 296-299(in Chinese).
[7] 周文娟,陈廷相,刘江,等. 压水堆松动件故障监测中水对碰撞波影响的研究[J]. 核动力工程,1998,29(6):509-512.
ZHOU Wenjuan, CHEN Tingxiang, LIU Jiang, et al. Research of collision wave influenced by water in PWR loose parts fault monitoring[J]. Nuclear Power Engineering, 1998, 29(6): 509-512(in Chinese).
[8] 杨将新,郑华文,曹衍龙,等. 基于自适应AR模型的核电站松动件报警方法[J]. 原子能科学技术,2010,44(6):701-705.
YANG Jiangxin, ZHENG Huawen, CAO Yanlong, et al. Alarming method of loose parts in nuclear power plant based on adaptive auto-regressive model[J]. Atomic Energy Science and Technology, 2010, 44(6): 701-705(in Chinese).

