箍筋约束混凝土本构研究的发展与展望

魏公涛

(同济大学 建筑工程系，上海 200092)

箍筋约束混凝土本构研究的发展与展望

魏公涛

(同济大学 建筑工程系，上海 200092)

箍筋约束作为一种被动约束方式，对于混凝土单轴受压峰值强度、峰值点应变和下降段延性有显著影响。通过历史和逻辑两条线索对箍筋约束混凝土研究的发展进行较为全面的阐述，并具体分析了若干典型本构模型。发现箍筋约束混凝土本构模型建立的主流思想为：将箍筋约束效应等效为均匀围压，并利用均匀围压这个媒介性变量建立配箍与应力应变全曲线关键参数(峰值强度、峰值点应变和下降段延性)之间的关系，此种建模方法形成于早期Richart的研究，并一直以来占主导地位。此外，通过采用不同模型预测某一试验结果，发现各模型的预测会产生显著的差别。基于此，建议更为深入的研究箍筋约束机理并采用物理机制更为明确的素混凝土本构曲线。

箍筋约束；混凝土全曲线；延性；物理机制

混凝土是土木工程中用量最大的材料，在各种土木建筑和设施中随处可见它的身影。虽然混凝土应用广泛且已有数百年历史,但其复杂的材料性质仍在研究当中，一些关键的科学问题仍然处于悬而未决的境地。由于混凝土材料的抗拉性能远低于其抗压性能,故其应用往往伴随着钢筋的身影,因此在混凝土材料的研究中包含了钢筋对于混凝土力学性质影响的研究,箍筋约束效应的研究就是其中一个比较经典的课题。

1 研究历史

从1903年considere发现螺旋箍筋可以有效约束混凝土开始，箍筋约束混凝土的研究已有100多年的历史，从时间和逻辑的角度可分为3个研究阶段：1920年～1970年为早期探索阶段，1980年为研究模式成熟阶段，1990年至今为约束模型向高强混凝土、高强箍筋发展阶段。

1.1 早期探索阶段

1928年，Richart[1]进行了液体围压约束下混凝土圆柱体轴压试验研究，根据试验结果，提出了著名的约束效应公式，

(1)

式中，fcc为受约束混凝土轴心抗压峰值强度，fc0为素混凝土轴心抗压峰值强度，k1为施加横向约束力对于抗压峰值强度的影响系数，fl为横向约束力。次年，Richart[2]对配置螺旋箍筋的圆柱体试件进行了试验研究，根据试验结果，Richart提出液体围压约束的公式亦可用于螺旋箍筋约束。Richart的研究具有奠基性的意义，为约束混凝土的研究提供了思路和方法。

从Richart的研究至20世纪70年代是约束混凝土第一个研究时期，这期间研究者们对于影响约束效果的因素进行了试验和理论研究，chan[3]、blume[4]、Roy和Sozen[5]等人考虑了横向钢筋的含量和屈服应力，Soliman和Yu[6]考虑了横向钢筋的含量、间距和被约束混凝土面积，1971年，Sargin[7]通过一批包含63个棱柱体试件的轴压试验，系统考虑了混凝土强度、箍筋含量、保护层、箍筋强度、箍筋表面是否光滑、浇筑方式这6个因素，并在模型中重点考虑了保护层厚度和应变梯度两个因素，Kent和Park[8]考虑了配箍率、箍筋相对间距(箍筋间距/混凝土核心较小尺寸)、箍筋强度和混凝土强度的影响。对于应力应变曲线方程形式，主要提出了3种[9]，1971年Sargin曲线[7]， 1973年Popovics曲线[10]，1971年Kent-Park曲线[8]。

这一时期的研究为之后的工作奠定了基础，主要包括:

(1)通过试验和理论摸索，提出了可行的考虑约束效应的建模方法。

(2)发现了两个关键现象，即存在弱约束区(图1中的阴影部位)和箍筋约束的被动性。

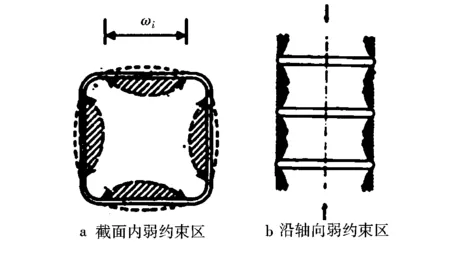
图1 箍筋约束效果图Fig.1 Change of confinement in section

(3)提出3种全曲线方程形式，为之后的全曲线形式选取奠定了基础。

1.2 研究模式成熟阶段

20世纪80年代是普通强度混凝土箍筋约束效应建模方法基本完善的时期，基于前一时期的研究所形成的基本认识和方法，这一时期的研究者们对于约束指标基本形成了共识，并且对于更深入的约束效率概念进行了研究。

箍筋约束混凝土存在约束效率的问题，在早期已经被认识到，即有效约束面积小于核心混凝土面积或者说存在弱约束区，但是并未被细致研究，只是通过箍筋相对间距(箍筋间距/较小的核心尺寸)来反映(Sargin 1971[7]，Park 1971[8])，1982年，sheikh[11]提出了有效约束面积概念，进而提出了反映约束效率的有效约束系数概念，用来反映箍筋约束尤其是方箍约束效果的折减，sheikh只考虑了沿轴向的折减

(2)

式中，s为箍筋间距，b为核心混凝土截面尺寸。1988年，Mander[12]对于此系数进行了改进，同时考虑截面内和轴向两方面的折减

(3)

式中，Ae为有效约束面积，Acc为核心混凝土面积，n为图1a中阴影区域个数即弱约束区个数，ωi为弱约束区长度，见图1a，bcx、bcy分别为核心混凝土截面两个方向尺寸，ρcc为纵筋配筋率(纵筋面积与核心混凝土截面面积比值)。

1988年，Mander[12]提出模型，以有效约束系数乘以配箍特征值作为唯一约束指标，这种方法被广泛所接受，同时Mander将应变率考虑进模型，并且认为约束与应变率不具有相互影响，后来的研究也基本沿用了这一方法(如S-R模型[13])。

1.3 约束模型向高强混凝土、高强箍筋发展阶段

随着混凝土强度的提高和高强混凝土的逐步广泛应用，从20世纪80年代末兴起了对于高强混凝土箍筋约束的研究。高强混凝土与普通混凝土相比延性较差，从而导致材料耗能能力较差，且无法形成有效的塑性铰，故通过箍筋约束来提高延性的研究具有重要意义。

高强混凝土与普通混凝土相比，箍筋约束效果有两个较为明显的区别，第一，相同配箍情况下，前者延性、峰值应力、峰值应变3个关键因素的提高不如后者明显，尤其是延性(Cusson&Paultre[14]，1994)；第二，基于第一个原因，同时为了防止过多配箍带来的钢筋笼堵塞(congestion of steel cage)现象，往往选用高强箍筋，这种做法导致了箍筋在应力应变曲线峰值点附近不屈服的现象。针对这两个问题，一些研究者提出了一些适用于高强混凝土的模型，如Yong et al.模型[15]，Cusson&Paultre模型[16]，史庆轩模型[17]，一些研究者还提出了同时适用于普通强度和高强混凝土的模型，如Saatcioglu&Razvi模型[18]，Legeron et al模型[19]。

2 典型模型

2.1 Kent-Scott-Park模型[20]

此模型是对Kent-park模型的改进，考虑了约束对于峰值强度和峰值点应变的增加

(4)

(5)

其中，

(6)

全曲线公式中下降段斜率参数Zm修正方法为

(7)

其中，h为截面尺寸，ρsv为体积配箍率。

图2 各模型应力应变全曲线示意图Fig.2 Stress-strain curve of several models

2.2 Mander模型[12]

模型在之前Kent-scott-Park、sheikh等模型的基础上进一步提出了更为合理的约束效率ke(有效约束系数,见式(3))，模型将等效约束力fl′与混凝土轴心抗压强度fc0的比值作为唯一的约束指标进行关键参数的修正

(8)

其中，

(9)

Mander模型比较全面合理的考虑了约束指标，且采用了单一的约束指标，模型较为简单实用，模型曲线见图2b。

2.3S-R模型[18]

S-R(1999)模型是对S-R(1992)模型[13]的改进，使之适用于各种强度混凝土和高强箍筋；等效围压公式中箍筋应力用峰值点处的实际应力取代屈服强度

(10)

其中，σyv为峰值点处箍筋实际应力，As为单肢箍筋面积，α为箍筋倾角，并建议了一个有效约束系数公式，其中考虑了纵筋影响，

(11)

其中，bc为受约束方向核心混凝土截面尺寸，sl为纵筋间距。

模型给出了峰值点处高强箍筋的应力公式，

(12)

其中，fsy为箍筋屈服应力。

S-R模型相对于其他模型更具有经验性，体现在有效约束系数公式和全曲线峰值点处箍筋应力公式均是数据直接拟合的结果，模型曲线见图2a。

2.4Legeron模型[19]

Legeron模型通过力学分析结合试验确定峰值点处箍筋应力σsv，并给出了直接的计算公式，避免了迭代计算箍筋应力(Cusson(1995))

(13)

其中，

(14)

其中，ρsey为所研究方向的箍筋有效配筋率，εc0为素混凝土全曲线峰值点处应变。

此模型适用于各种强度混凝土，且峰值点处箍筋应力的公式更具明确的物理意义，模型曲线见图2c。

2.5 史庆轩模型[18]

模型亦采用了单一的约束修正指标，即等效约束力与素混凝土轴压强度比值；同时建议了峰值点处箍筋应力公式，与S-R模型建议的公式形式一致，且均为单纯的数据拟合结果；峰值点处箍筋应力

(15)

引入了Mander建议的有效约束系数公式，得到约束指标：

(16)

其中，Asvx和Asvy分别为截面两个方向箍筋折算面积，bx、by分别为截面两个方向箍筋轴线间距，有效约束系数ke采用Mander建议的形式。史庆轩模型引入了有效约束系数，较以往国内的模型更完善，且为国内高强箍筋约束模型的研究奠定了基础，模型曲线见图2d。

3 不同模型预测同一试验结果

已有的箍筋约束混凝土模型多为经验型模型，建模思路大多遵循了Richart所建议的模式：将箍筋约束等效为均匀围压，进而建立约束与混凝土本构关键参数的函数关系。此种建模方式的经验性使得研究者在选择函数关系的过程中具有很强的随意性，并且研究者们建模所依据的试验数据往往由单一试验所得，故诸多模型虽可以很好的符合建模所依据的试验结果，却无法很好的预测其他试验结果。

例1：选取Cusson所做高强混凝土箍筋约束试验(1994)，并用多个模型进行预测，预测结果与试验结果进行对比见图3。

图3 不同模型预测Cusson试验结果对比图Fig.3 Comparison of models and experiment results

几个主要参数的模型预测值与试验值对比见表1(延性指标为下降段50%峰值强度的应变与峰值点应变比值)。

例2：选取杨坤等人所做的试验(2013)，试验结果与多个模型预测结果对比见表2。

表1 例1：主要参数的模型预测值与试验值对比表

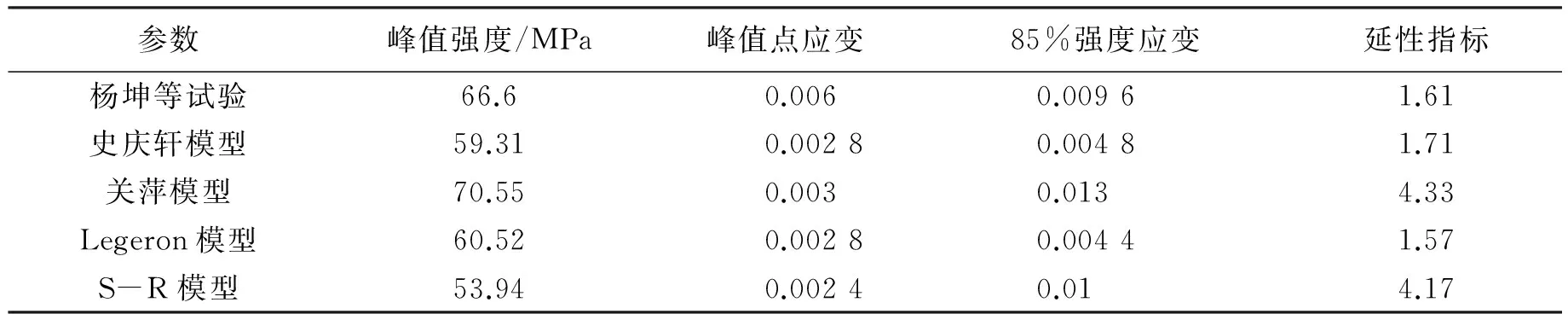
表2 例2：主要参数的模型预测值与试验值对比表

以上两个例子显示用各模型预测同一试验会有明显偏差：关萍模型对峰值强度的预测偏大，史庆轩模型下降段前期较陡，后续延性偏大，而S-R和Legeron模型对峰值强度预测偏于保守。箍筋在上升段前半部分其约束作用微弱，各模型的预测均较为准确；当应变接近峰值点时，混凝土出现明显裂缝，横向应变增大，箍筋开始起显著作用，各模型对约束效果的预测开始出现较大偏差。

4 结论

(1)箍筋约束混凝土轴压本构模型的主流建模思路为：根据箍筋约束试验结果建立等效约束力与本构模型的关键参数(峰值强度、峰值点应变和延性指标)之间的经验关系。经过近百年的研究，箍筋约束混凝土的研究成果已经应用于各国的规范(GB50010-2010[22]、ACI318-05[23]、NZS3101-1995[24])。

(2)研究者在建模过程中往往依据某一特定试验建立经验模型，从而在预测其他试验结果时必然具有相当的局限性。

(3)箍筋约束混凝土轴压力学性能仍然需要进一步研究，这依赖于混凝土本构理论的发展和对箍筋约束物理机制的更深入认识。

[1] Richart F E, Brandtzaeg A, and Brown R L. A Study of the Failure of Concrete under Combined Compressive Stresses[R].University of Illinois Engineering Bulletin,1928(185):104.

[2] Richart F E, Brandtzaeg A and Brown R L. The Failure of Plain and Spirally Reinforced Concrete in Compression[R].University of Illinois Engineering Bulletin,1929(190):74.

[3] Chan W L. The Ultimate Strength and Deformation of Plastic Hinges in Reinforced Concrete Frameworks[J].Magazine of Concrete Research, 1955,7(21):121-132.

[4] Blume J A, Newmark A L and Corning L H. Design of multistory Reinforced Concrete Buildings for Earthquake Motion[M].Chicago:Portland Cement Association,1961.

[5] Roy H and Sozen M A. Ductility of Concrete[C].Miami: Proceedings of the International Symposium on Flexural Mechanics of Reinforced Concrete, 1964:213-224.

[6] Soliman M T M and Yu C W. The flexural Stress-Strain Relationship of Concrete Confined by Rectangular Transverse Reinforcement[J].Magazine of Concrete Research, 1967,19(61):223-238.

[7] Sargin M, Ghosh S K and Hander V K. Effects of Lateral Reinforcement upon Strength and Deformation of Concrete[J].Magazine of Concrete Research, 1971, 23(75-76):99-110.

[8] Kent D C and Park R. Flexural Members with Confined Concrete[J].Journal of Structural Division, 1971,97(ST7):1 969-1 990.

[9] 李晓光.矩形箍筋约束混凝土模型的改进探讨[D].重庆：重庆大学，2011.

[10] PoPovics S. A numerical Approach to Complete Stress-Strain Curve of Concrete[J].Cement and Concrete Res,1973,3:583-599.

[11] Sheikh S A, Uzumeri S M. Analytical Model for Concrete Confinement in Tied Columns[J].Journal of Structural Division, 1982,108(ST102):2 703-2 722.

[12] Mander J B, Priestley M J Nand Park R. Theoretical Stress-Strain Model for Confined Concrete[J].Journal of Structural engineering, 1988,114(8):1 804-1 826.

[13] Saatcioglu M, Razvi R. Strength and Ductility of Confined Concrete[J].Journal of Structural Engineering, 1992,118(6):1 590-1 607.

[14] Cusson D and Paultre P. High-strength Concrete columns confined by rectangular ties[J].Journal of Structural Engineering, 1994,120(3):783-804.

[15] Yong Y K, Nour M G and Nawy E G. Behavior of laterally confined high-strength concrete under axial loads[J].Journal of Structural Engineering, 1988,114(2):332-351.

[16] Cusson D and Paultre P. Stress-strain model for confined high-strength concrete[J].Journal of structural Engineering, 1995,121(3):468-477.

[17] 史庆轩，王南，田园，等.高强箍筋约束高强混凝土轴心受压应力-应变全曲线研究[J].建筑结构学报，2013,34(4)：144-151.

[18] Saatcioglu M and Razvi S R. Confinement Model for High- strength Concete[J].Journal of structural Engineering, 1999,125(3):281-289.

[19] Legeron F and Paultre P. Uniaxial Confinement Model for Normal- and High-Strength Concrete Columns[J].Journal of structural Engineering, 2003,129(2):241-252.

[20] Scott B D, Park R, Priestley M J N. Stress-Strain behavior of Concrete Confined by overlapping Hoops at Low and High Strain Rates[J].ACI Journal, 1982,79(2):13-27.

[21] 关萍，王清湘，赵国藩.高强约束混凝土应力-应变本构关系的试验研究[J].工业建筑，1997,27(11)：26-29.

[22] 规范编写组.GB50010-2010混凝土结构设计规范[S].北京：中国建筑工业出版社，2010.

[23] ACI committee 318. ACI318-05Building code requirements for structural concrete and commentary[S].Michigan,ACI,2005.

[24] NZS3103. NZS3101-1995The design of concrete structures[S].New Zealand:NZS,1995.

(责任编辑：李华云)

The Development and Prospect of Transverse Steel Confined Concrete Stress-Strain Model

WEI Gongtao

(Department of Building Engineering, Tongji University, Shanghai 200092, China)

As a passive confinement method, transverse steels confinement produces significant effects on the behavior of concrete under axial compression, including the improvement of the maximum stress, the corresponding strain and the ductility. From both historical and logical perspectives, the development of hoop confined concrete is summarized, and several important models are studied specifically. The main method in modeling adopted by most studies is: using equivalent mean perimeter pressure to represent the confinement effect produced by lateral steels, and then connect with several key parameters of the stress-strain relation. This modeling method was firstly suggested by Richart in 1929, then it's been accepted by most studies. Because of that most of the models are empirical ones, the prediction about a specific case by different models will be obvious different. Based on this, further research of confinement from mechanics perspective and a more reasonable concrete model are needed in modeling hoop confined concrete.

hoop confinement, concrete stress-strain curve, ductility, physical mechanism

2014-01-20

高等学校博士学科点专项科研基金新教师类课题(2012007212007)

魏公涛(1990-)，男，山东临沂人，硕士生，主要从事混凝土材料非线性行为研究及结构分析。

TU375

A

1671-5322(2014)02-0042-06