抽取频域关系的正确推导

柴晓东，袁 晓

(1.黄河科技学院 国际学院，河南 郑州 450063; 2.四川大学 电子信息学院，四川 成都 610065)

抽取频域关系的正确推导

柴晓东1，袁 晓2

(1.黄河科技学院 国际学院，河南 郑州 450063; 2.四川大学 电子信息学院，四川 成都 610065)

主要介绍序列信号抽取频域关系的正确推导。首先从学生课堂自行推导抽取频域关系时易犯的普遍错误出发，找出其错误的原因,然后从模拟域和数字域两个方面分别来推导它们的正确关系。在模拟域里，对模拟信号进行抽样，从抽样的角度来分析;而在数字域里，则是直接对序列信号进行分析。模拟域和数字域的两种推导方法，采用相对较为简单的采样定理法和卷积法。最后对两种推导方法得到的结果进行对比，并验证其正确性。

抽取;采样;抽取因子;卷积

抽取与内插是现代数字信号处理理论中两个重要的基本概念。序列信号抽取的频域关系，在多抽样率[1]信号处理技术、控制理论、电路与系统理论、滤波器组理论、子波分析及通信工程等领域广泛应用。在很多相关的本科、研究生教材中都给出了序列信号抽取的频域关系式，但对其推导过程的介绍却不是很详细，读者不易理解。在长期的课堂教学中发现，不仅仅是本科生，包括研究生在不知道正确的抽取频域关系情况下，自行推导其关系时，都会采用一种相似的方法，得到错误的结果。如果不进行深入分析，很难发现错误的原因。文章从学生课堂自行推导抽取频域关系时采用的普遍方法入手，从模拟域和数字域两个方面分别来推导其正确关系，从而使读者更深刻的理解抽取的本质。

1 学生课堂自行推导的错误及原因

1.1 学生课堂的变量代换法推导方法

在长期的教学实践中，我们发现，学生在不知道抽取频域关系的情况下，课堂自行推导其关系时，普遍采用变量代换法。

序列信号x[n]经M倍抽取后，得到新序列信号y[n]，即

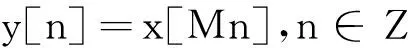
(1)

其中M称为抽取因子。式(1)是抽取的时域表达式，其频域表达式又如何呢？

根据离散傅里叶变换(DFT)的定义，可以得到

(2)

作变量代换

(3)

得

(4)

这是课堂上几乎所有学生的推导结果。该结果正确吗？

1.2 变量代换法推导结果正确性的检验

要检验学生变量代换法推导结果的正确性，可以从理论和实践两个方面来检验。

从理论上来考察。对于有限长度的序列x[n]进行M倍抽取得到的y[n]，时域长度被压缩M倍，其频谱应当被扩展M倍，从这一点看来，上式的正确性似乎是无可厚非的。但是，任何序列信号的频谱函数都是2π―周期的连续函数。而X(ω/M)却是以2πM为周期的函数，显然与Y(ω)是2π―周期的函数相矛盾，由此可以肯定式(4)是不正确的。

从实践方面来考察。给定一有限长度的序列信号x[n]及其对应的|X(ω)|(实线表示)与|X(ω/2)|(虚线表示)，如图1所示。y[n]=x[2n]及其对应的|Y(ω)|的示意图如图2所示。

图1 x[n]及其对应的|X(ω)|与|X(ω/2)|示意图Fig.1 x[n] and corresponding |X(ω)| and |X(ω/2)|

图2 x[2n]及其对应的|Y(ω)|示意图Fig.2 x[2n] and corresponding |Y(ω)|

由图1和图2所示，很显然，|X(ω/2)|与|Y(ω)|的图形不一样。这也说明式(4)是错误的。

1.3 错误原因的分析

变量代换法究竟错在哪里呢？现在对式(4)进行变换，找一找错误的原因。

(5)

由上式可以看出，错误的原因出在变量代换过程中。从式(5)中，可以很直接的看出，求和指标m是分两部分的，即m为M的整数倍和m不为M的整数倍，这两部分结合在一起构成了求和指标m是取遍所有整数。在求Y(ω)时，由变量代换式(3)可知，由于n为整数，所以要求m只取M的整数倍。这就要求式(5)中，m不为M的整数倍时x[m]的取值全为0，但由于x[m]在m不为M的整数倍时，其取值不全为0，从而使式(5)中的后一项为多余项。学生在课堂推导时，恰恰忽视了这一点，从而得出了错误的关系式(4)。

2 两种正确的推导方法

抽取频域关系的推导方法，在很多教材中都不尽相同。例如，宗孔德著的《多抽样率信号处理》中采用的是数字域推导方法[2]，胡广书著的《现代数字信号处理教程》中采用的是Z域推导方法[3],而奥本海姆等著《离散时间信号处理》中则采用的是模拟域推导方法[4]，其共同不足之处是过程不详细，方法较为复杂，不易理解。下面介绍两种比较简单，且容易理解的方法。

2.1 采样定理法——模拟域推导方法

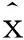
(6)

式中Ts是采样周期，根据序列信号傅里叶变换与连续信号傅里叶变换的关系[7]可以得到

(7)

同理，抽取后得到的序列信号y[n]完全可以由模拟信号xa(t)以采样周期MTs进行采样而得到，即

y[n]=x[Mn]=xa(nMTs) n∈Z

(8)

因此，只要找出式(7)与式(8)之间的关系，就可以得到Y(ω)与X(ω)的关系。

利用学过的数学知识，可以把式(8)中的求和指标r写成如下的形式

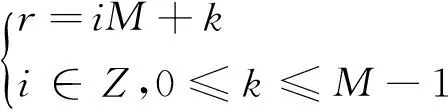
(9)

很显然，这样得到的r仍然是一个整数并且取遍所有整数，从而有

将上式结果与式(7)相对照，可以得到Y(ω)与X(ω)之间的关系

(10)

这就是序列信号抽取的频域关系式。

现在来检验一下式(10)是否是2π―周期的函数。

而

显然，Y(ω)= Y(ω+2π)，所以Y(ω)仍然是2π―周期的函数。

2.2 卷积法——数字域推导方法

抽取实质上是一个再采样(resampling)过程，不是在模拟域中的采样，而是在数字域中的采样。抽取的等效模型如图3所示。图中的函数pTs(t)、pM[n]都称为理想的采样函数。

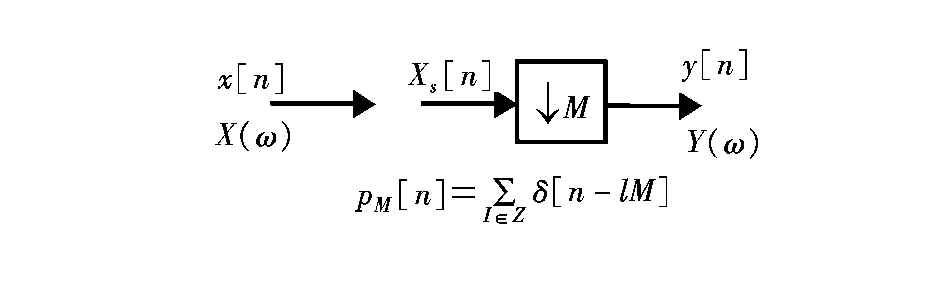
图3 抽取的等效模型Fig.3 Decimation equivalent model

由于pM[n]=∑δ[n-lM],l∈Z，因此，对原始序列x[n]的直接抽取y[n]=x[Mn]，与对数字采样得到的中间过渡序列xs[n]的抽取所得到的结果是完全一样的，即y[n]=xs[Mn]，其中

xs[n]=x[n]·pM[n]。

为了求出序列信号抽取正确的频域关系，需要求出pM[n]的频谱函数。根据离散傅里叶级数正、反变换公式[4]可得

(11)

其频谱函数为

(12)

由频域卷积定理[8]可得

(13)

由于y[n]=x[Mn]是经过xs[n]时域压缩M倍得到的。根据学过的数字信号处理的基础知识可知，在频域内，Y(ω)应该是Xs(ω)经过频域扩展M倍得到[9]。

3 结语

从时域关系看，对序列信号进行抽取，其实质是降低信号的抽样率，减少原始数据，将原始信号进行压缩,从频域关系来看，抽取后信号频谱是抽取前信号频谱的延拓，其差别只在频率尺度上不同。教学实践证明，在众多的推导方法中，上述两种推导方法学生理解起来更容易，更能普遍为学生所接受和掌握。随着教学模式的多样化，此部分内容若用动画来课堂演示，对课堂教学及学生学习，将是一种更有益的帮助。

[1] 王向昆.多抽样率数字信号处理在Galileo导航信号接收中的应用实现[J].数字技术与应用，2012，4：51-52.

[2] 宗孔德.多抽样率信号处理[M].北京：清华大学出版社，1996.

[3] 胡广书.现代数字信号处理教程[M].北京：清华大学出版社，2004.

[4] 奥本海姆.离散时间信号处理[M].黄建国，译. 北京：科学出版社，1998.

[5] 谢海霞，孙志雄.多相抽取滤波器的FPGA实现[J].电子器件，2012，35(3)：331-333.

[6] 杨巧宁，李学斌，王学伟.信号与系统中抽样定理的教学探讨[J].电气电子教学学报，2012，34(3)：109-111.

[7] 丁玉美，高西全.数字信号处理[M].西安：西安电子科技大学出版社，2005.

[8] 潘文诚，徐鸿飞，李津蓉，等.信号类课程教学中连续与离散的类比性[J].浙江科技学院学报，2012，24(4)：323-328.

[9] Crochiere R E， Rabiner L R. Interpolation and decimation of digital signals: a tutorial review[C].Proc IEEE,1981，69：300-331.

(责任编辑：张英健)

On the Formula of the Decimation in the Frequency-Domain

CHAI Xiaodong1, YUAN Xiao2

1.Intetnational School, Huanghe S&T College, Zhengzhou Henan 450063, China;2.College of Electronic and Information, Sichuan University, Chengdu Sichuan 610065, China

This paper mainly introduces the reasonable derivation of the relationship of decimation in the frequency-domain. Firstly, we begin with the faults which the students made in the classrooms by themselves when deriving the relationship. Secondly, we derive their correct relationships from the analog and the digital domain respectively. In the analog domain, we first sample the analog signal and then analyze it from the angle of the sample. While in the digital domain, we analyze the sequence signal directly. For the two deduced methods in analog and digital domain, in the paper we use relatively simple methods based on sampling and convolution. Finally, we compare the results of these two methods, and verify its accuracy.

decimation; sampling; decimation factor; convolution

2013-10-29

柴晓东(1980-)，男，河南郏县人，助教，主要研究方向为计算机教学。

TN911.72

A

1671-5322(2014)02-0038-04