窄矩形通道内Ledinegg不稳定性实验研究
陈 冲,高璞珍,谭思超,黄 栋,余志庭,兰 述
(哈尔滨工程大学 核安全与仿真技术国防重点学科实验室,黑龙江 哈尔滨 150001)
流动不稳定性是指,在一个质量流密度、压降特性和空泡份额之间存在着热力学与流体动力学相联系的两相流系统中,流体受到一微小的扰动后所发生的流量漂移或以某一频率的恒定振幅或变化振幅进行的流量振荡[1]。研究表明[2-3],两相流不稳定性流动中Ledinegg不稳定性是比较常见的,1938年Ledinegg[4]研究了这种不稳定性,其研究发现,在特定的条件下流道内部的压降-流量特性曲线存在一负斜率区,在这个负斜率区内通道的压降并非流量的单值函数,会出现一个压强值对应多个流量值的现象,即发生流量飘移。
流动不稳定性是反应堆运行和事故工况中均有可能出现的一种有害的热工现象。Ozawa等[5]和Daleas等[6]认为流动不稳定性能导致临界热流密度(CHF)提前发生从而对设备和堆芯安全造成重大的威胁;Wu等[7]和Bergles等[8]的研究表明,微通道较常规大通道更易发生流动不稳定性,使机械部件和传热管破损。
现有的文献在研究流道内流量漂移现象时,对竖直加热圆管内的流动进行了较充分的研究,但对竖直窄矩形通道内Ledinegg不稳定性的研究相对较少,本文以现有的研究为基础,通过实验和理论两方面对窄矩形通道Ledinegg不稳定性进行分析。
1 实验装置及实验步骤
1.1 实验装置

图1 实验装置示意图
实验回路如图1所示,由主泵、稳压器、预热器、实验段及冷凝器等组成。流体在预热器内加热至设定值后流入实验段继续加热,再经冷凝器冷却后流回主泵入口,完成1个循环。利用直流电源直接加载于实验通道上使其保持恒定热流密度加热状态。实验段与回路及测压管之间通过四氟乙烯法兰连接,既能使实验段和回路其他部分保持绝缘,又可保证测压管内流体温度不受实验段加热的影响,整个回路采用保温棉进行保温,以减少热损失。
实验段为尺寸2 mm×40 mm×1 000 mm的窄矩形通道,热电偶与入口的距离为L/Dh=37、140、201、242、284、307(L为实验段长度;Dh为通道当量直径),引压孔的编号从入口到出口分别为1、4、5,与入口的距离为L/Dh=52、258、318,可测量1~4段压差p14和4~5段压差p45。使用电磁体积流量计测量工质的流量,其相对误差在±0.3%以内;压降测量使用两种不同的压力传感器,其量程分别为10 kPa和30 kPa,其相对误差均在±0.2%之内;6组热电偶测量误差在±0.3 ℃以内。
实验系统压强pin为0.4~1.0 MPa,质量流量G为0.05~0.6 kg/s,过冷度tsub为40~80 ℃,热流密度q为170~300 kW/m2。
1.2 实验步骤
在恒定热流密度、入口过冷度、系统压强情况下,调节主泵的转速,测量实验段的流动压降和质量流量间的关系可得到窄矩形通道内部特征曲线;改变热流密度、入口过冷度、系统压强,然后重复上述实验可得不同工况下窄矩形通道内部特征曲线。
2 窄矩形通道内部静态分析

图2 圆通道内部特征曲线
圆通道内部特征曲线示于图2,通道两相压降-流量曲线与全液相压降-流量曲线的交点即为过冷沸腾起始点ONB,随着质量流量的继续减小,将会导致通道内的空泡份额明显增加,即达到明显空泡份额点OSV,在单相与两相转折区域的最低点即为流动不稳定起始点OFI。Stoddard等[9]认为在常规圆通道中OSV可作为OFI的保守判定准则,即OSV和OFI区别不大,但ONB和OSV是两个不同特征的点。
窄矩形通道内部特征曲线示于图3。比较图2、3可发现,通道内部特征曲线略有不同,在圆通道全液相和两相的转折区域,曲线的斜率出现了明显的变化,而窄矩形通道在转折区域的斜率并无变化,且与全液相压降-流量曲线重合,说明窄矩形通道中ONB、OSV和OFI 3点极为接近,不易区分。图4为窄矩形通道发生Ledinegg不稳定时p14和p45的变化情况,由图可看出,当通道发生过冷沸腾时,p45在很短的时间内超过p14,无缓变的过程,这一点也证明了ONB、OSV、OFI 3点极为接近,不易区分。这可能是由于窄矩形通道的尺寸很小抑制了气泡的生长,沸腾起始点ONB所需的壁面过热度和热流密度高于常规通道的,这样就会使窄矩形通道ONB向低流量方向偏移;窄矩形通道尺寸很小,在通道中一旦出现核态气泡就会出现OSV,OSV向高流量方向偏移,同时,OSV的出现会使实验段的压降迅速升高,导致流量突然降低。

图3 窄矩形通道内部特征曲线
2.1 热流密度的影响
图5为pin=1.0 MPa、tsub=60 ℃时热流密度对窄矩形通道内部特征曲线的影响。由图5可见,特征曲线为N型,在全液相区域,压降-流量曲线的斜率为正值,在ONB之后,压降-流量曲线的斜率为负值,在一定质量含气率情况下,曲线达到极大值(图中A′、B′)后又逐渐降低。随热流密度的提高,气泡的生成和生长的速率很快,同时在高宽比很小的窄矩形通道中气泡的产生会给压降带来巨大的影响,使沸腾起始点A和B向高质量流量移动,同时极值点A′、B′与A、B之间的压降Δp和质量流量差ΔG依次提高,且变化的幅值较大,导致在两相负斜率区随热流密度的增加,曲线斜率减小。根据Ledinegg不稳定性准则[4],得出窄矩形通道中随热流密度的增加,其流动稳定性变差,由于Δp和ΔG的增加,流动不稳定性产生时,流量出现大振幅和长周期的波动。
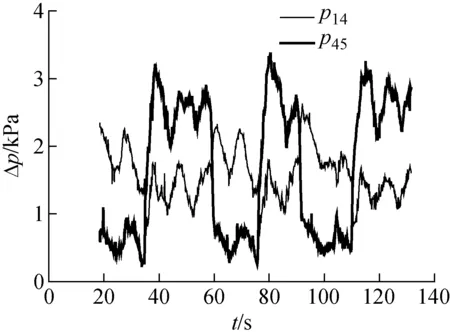
图4 压降随时间的变化

图5 热流密度对窄矩形通道内部特征曲线的影响
2.2 系统压强的影响
系统压强对窄矩形通道内部特征曲线(tsub=60 ℃,q=253 kW/m2)的影响如图6所示。随系统压强的增加,Δp和ΔG均减小,但变化的幅度不同,压强越大通道内部特征曲线越平滑,系统越稳定,由于Δp和ΔG均减小,即使出现Ledinegg不稳定性其流量波动的幅值也较小。压强小于0.7 MPa时,内部特征曲线负斜率区的斜率随压强的增加,压降梯度变化较大,即当系统压强小于0.7 MPa时,系统的不稳定性对压强的变化比较敏感。

图6 系统压强对窄矩形通道内部特征曲线的影响
2.3 过冷度的影响

图7 入口过冷度对窄矩形通道内部特征曲线的影响
入口过冷度对窄矩形通道内部特征曲线(pin=0.52 MPa,q=170 kW/m2)的影响如图7所示。随入口过冷度的增加,单位流体达到沸腾起始点所需的能量增加,沸腾起始点ONB逐渐向低质量流量移动,同时Δp和ΔG同步减小,同一区域内部特征曲线的斜率基本相同,根据Ledinegg不稳定性准则[4],说明过冷度对窄矩形通道Ledinegg不稳定性发生的概率的影响很小,只会对流量漂移的振幅有影响,这一点与常规圆管通道的规律不同,Kakac等[10]认为在常规通道中随过冷度的增加,通道的内部特征曲线负斜率区斜率减小,系统的不稳定性增加,所以为了提高稳定性,通常会在进口段放置预热器。
3 窄矩形通道内部特征数学模型
为更清楚地认识特征曲线的数学特性,忽略窄矩形通道内的加速压降和重力压降,仅考虑摩擦压降Δpf,设窄矩形通道的高为a、宽为b。
矩形通道内的摩擦压降主要包括单相摩擦压降和两相摩擦压降:
Δp≈Δpf=Δpsp+Δptp
(1)
其中,Δpsp和Δptp分别为单相液体段摩擦压降和两相段摩擦压降。
单相液体段的长度Lsp可简化为:
Lsp=G(hf-hin)/ql
(2)
两相段长度为:
(3)
出口含气率为:
(4)
单相和两相平均比容:
νf+νin)
(5)

(6)
实验段内的总压降Δp为:

(7)
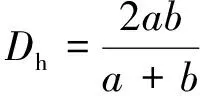
(8)
其中,W、ff、ftp、νg、νf和νin分别为质量流速、单相摩阻系数、两相摩阻系数、饱和汽比容、饱和水比容和入口比容。
由图3可看出窄矩形通道内部特征曲线类似是一元三次曲线,假设:
Δp=f(G)=CG3+EG2+FG
(9)
将式(2)~(6)代入式(7),并与式(9)进行对比,可得:
(10)
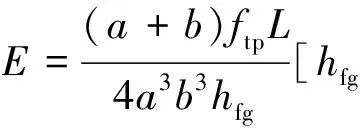
(11)

(12)
由式(9)~(12)可得到压降-流量曲线为一元三次曲线,在一定的参数条件下,可构成N型曲线。从数学角度上分析,一元三次曲线有3个根,可能全部是实根,也可能1个实根2个虚根。解的特征性表明,在某组合压降Δp下,仅存在1个实根,即对应1个流量值,则系统是稳定的,若为3个根,则系统会发生流量漂移。欲在任何外部特性曲线下保持流量稳定,则必须满足单值条件,压降随流量的增加单调上升或仅有1个拐点存在,即压降与流量一一对应。它的数学条件有两种:

对式(9)求导,得:
(13)
式(13)为一个一元二次函数,欲使式(9)满足单值数学条件,对于式(13)应满足:
Δ=E2-3CF≤0
(14)
式(14)即为窄矩形通道系统稳定的数学条件,可通过调整不同的系统参数,来改变系数C、E、F,使其满足式(14),以增强系统的稳定性。系统压强升高,会减小气液比容差νfg=νg-νf,C和F减小,E增大,对于式(14)形成的条件有利,系统的稳定性增强,这与实验现象吻合。
4 结论
在实验段系统压强pin为0.4~1.0 MPa、流量G为0.05~0.6 kg/s、过冷度tsub为40~80 ℃的实验工况下,进行了一系列实验,得出以下结论。
1) 在高宽比很小的窄矩形通道中ONB、OSV和OFI 3点距离很近,很难区分。
2) 窄矩形通道中随热流密度的增加和压强的减小,Ledinegg流动不稳定性发生的概率增大,流量漂移的振幅也增大,与常规圆管不同,过冷度只对流量漂移的振幅有影响而对窄矩形通道Ledinegg不稳定性发生概率影响很小。
3) 在压强小于0.7 MPa区域,内部特征曲线的负斜率随压强的增加,压降梯度变化较大,系统的不稳定性对压强的变化比较敏感。
4) 窄矩形通道内流动稳定的数学条件为E2-3CF≤0,根据系统稳定的数学条件,可通过改变不同的数学参数,来提高系统的稳定性。
参考文献:
[1] 俞冀阳,贾宝山. 反应堆热工水力学[M]. 北京:清华大学出版社,2011:196-197.
[2] BOURE J A, BERGLES A E, TONG L S. Review of two-phase flow instability[J]. Nuclear Engineering and Design, 1973, 25(5): 165-192.
[3] COLLINS D B, GACESA M. Hydrodynamic instability in a full-scale simulated reactor channel[J]. Proc Inst Mech Eng, 1969, 19(7): 69-70.
[4] LEDINEGG M. Instability of flow during natural and forced circulation[J]. Die Waerme, 1938, 61(8): 891-898.
[5] OZAWA M, UMEKAWA H, MISHIMA K, et al. CHF in oscillatory flow boiling channels[J]. Inst Chem Eng Symp Ser, 2001, 79(2): 389-401.
[6] DALEAS R S, BERGLES A E. Effects of upstream compressibility on subcooled critical heat flux[R]. New York: ASME, 1965.
[7] WU H Y, CHENG P. Boiling instability in parallel silicon microchannels at different heat flux[J]. Int J Heat Mass Transfer, 2004, 47(6): 3 631-3 641.
[8] BERGLES A E, KANDLIKAR S G. On the nature of critical heat flux in microchannels[J]. J Heat Transfer, 2005, 127(6): 101-107.
[9] STODDARD R M, BLASICK A M, GHIAASIAAN S M. Onset of flow instability and critical heat flux in thin horizontal annuli[J]. Experimental Thermal and Fluid Science, 2002, 26(4): 1-14.
[10] KAKAC S, CAO L, AVELINO M R. The effect of inlet subcooling on two-phase flow dynamic instabilities in-tube boiling systems[J]. Low Temperature and Cryogenic Refrigeration, 2003, 68(6): 131-144.

