蒸汽发生器传热管束过冷沸腾区两相流动数值模拟
王成龙,丛腾龙,田文喜,秋穗正,苏光辉
(西安交通大学 能源与动力工程学院,陕西 西安 710049)
蒸汽发生器作为一、二回路的枢纽,在核反应堆系统中起着重要的作用。首先,它是热交换设备,可将一回路冷却剂携带的热量传递给二回路给水。其次,它还是承压边界,对放射性产物起到屏蔽作用。在蒸汽发生器长时间运行过程中容易出现传热管的振动、磨损、疲劳以致破裂,影响蒸汽发生器的安全可靠性。因此,研究蒸汽发生器传热管束内流体的流动换热特性十分重要。
目前,国际上对蒸汽发生器传热管束内流动换热特性已开展了广泛的研究,由于实验研究的局限性,绝大部分工作是利用CFD方法对蒸汽发生器传热管束内流动进行数值模拟。戴玉龙等[1]利用FLUENT数值模拟了梅花形孔板支撑换热器壳程单相流动换热特性。Hassan等[2]基于有限元方法研究了不同结构、不同尺寸支撑孔板内详细的流动特性。Sun和Li等[3-4]采用两流体模型,利用FLUENT数值模拟了蒸汽发生器方形排列传热管束内流体的流动换热特性,并对四叶梅花孔支撑板进行简化,研究了梅花孔支撑板对蒸汽发生器热工水力特性的影响。从以上研究工作可看出,对于蒸汽发生器内流动换热特性的研究存在诸多不足,如二次侧详细的流动沸腾现象,未简化的梅花孔支撑板对蒸汽发生器热工水力特性的影响,不同入口过冷度对蒸汽发生器传热特性的影响等。鉴于此,本工作在文献[5]基础上,采用两流体欧拉数学模型结合Kurul等[6]提出的RPI壁面沸腾模型,运用ANSYS CFX 12.0计算软件,对蒸汽发生器三角形排列传热管束内的流动沸腾现象进行精确的数值模拟,研究梅花孔支撑板和不同入口过冷度对蒸汽发生器热工水力特性的影响。鉴于国际上采用精确数值模拟的方法还未实现过冷沸腾区与泡核沸腾区的准确过渡,因此本研究工作只针对过冷沸腾区。
1 数学物理模型
对于蒸汽发生器二次侧流动沸腾换热,采用两流体欧拉数学模型。对于壁面上的过冷沸腾采用RPI壁面沸腾模型,紊流采用壁面剪切应力模型(SST),其具体模型介绍及控制方程参见文献[5]。
2 几何模型及网格划分
图1示出蒸汽发生器传热管束几何模型,计算区域包括一次侧、管壁、二次侧和梅花孔支撑板。支撑板为三叶梅花孔结构,厚1.5 cm。管束呈三角形排列,间距为24.89 mm,长度为1 m。高温的一次侧流体从底端流入,将热量通过管壁传递给二次侧流体。二次侧流体温度上升,最终在一未知高度处发生过冷沸腾。
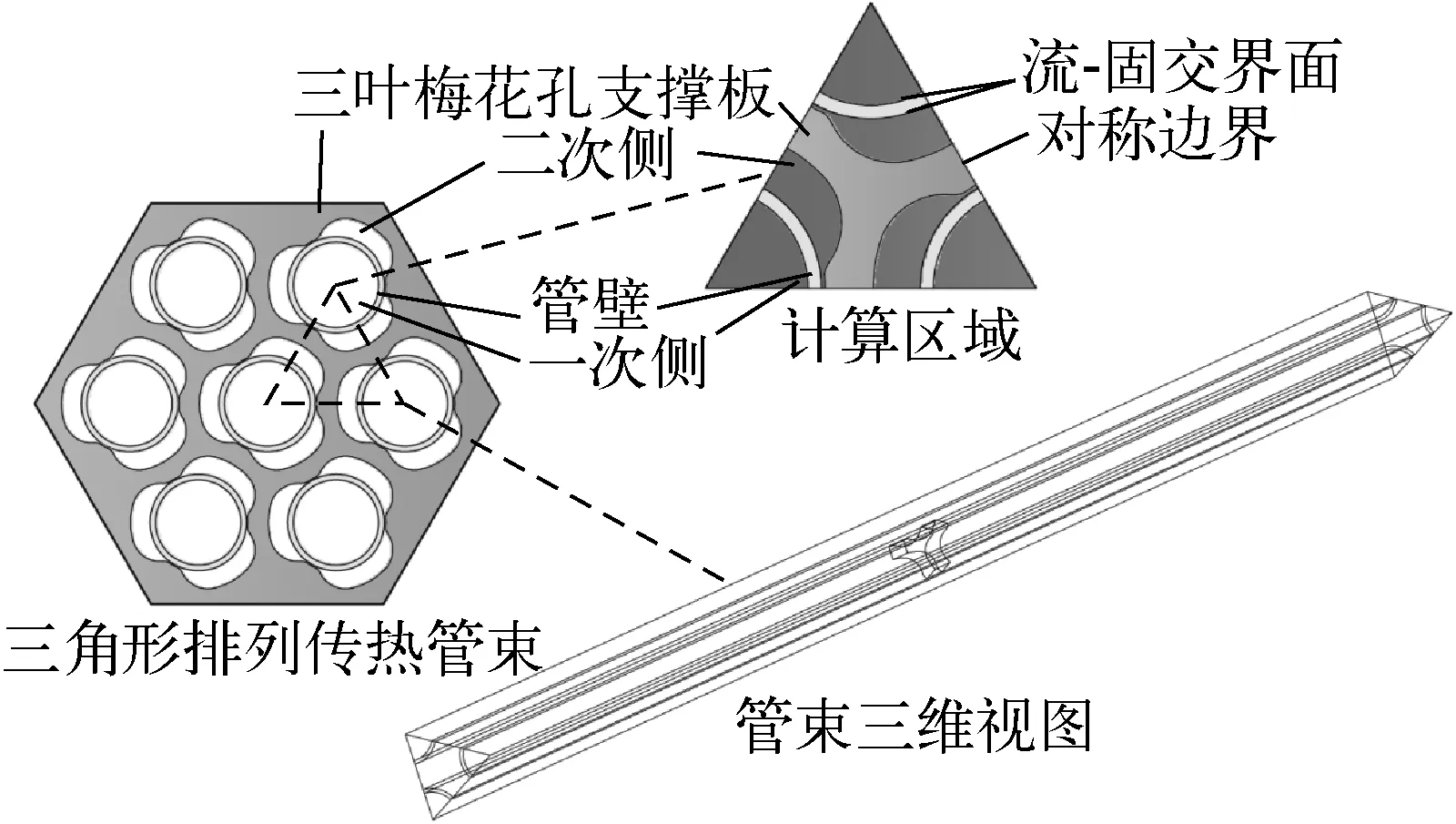
图1 蒸汽发生器传热管束几何模型
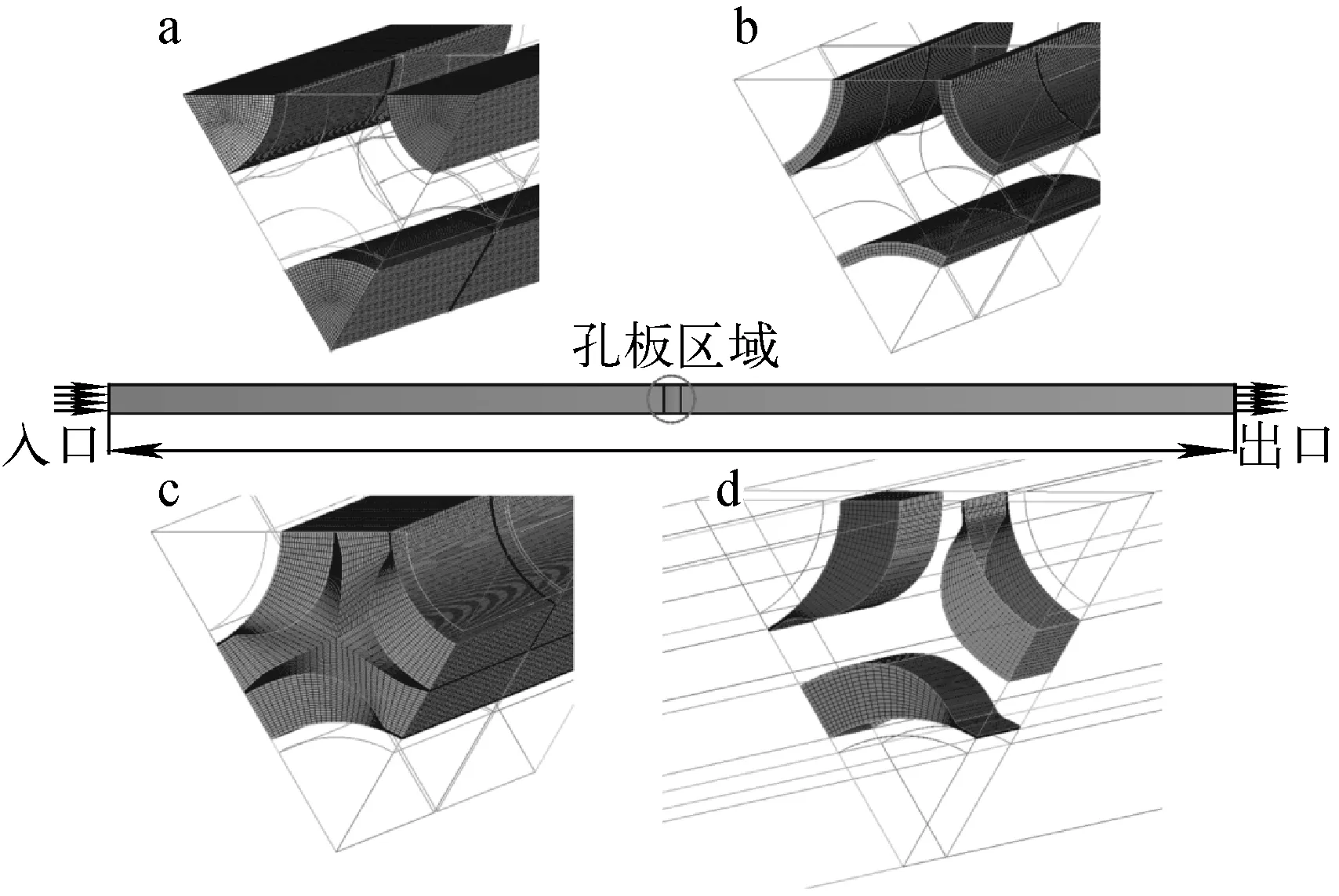
a——一次侧;b——管壁;c——二次侧;d——梅花孔支撑板
网格划分示于图2。网格采用结构化的六面体网格,质量大于0.5。网格入口边界条件为速度入口边界条件,出口边界条件为压力出口。一次侧壁面边界条件设置为无滑移壁面。二次侧壁面边界条件(包括加热壁面和梅花孔支撑板),对于液相设置为无滑移壁面边界条件,对于气相设置为滑移壁面边界条件。对于管壁,为便于收敛,底面设置为二次侧入口温度,顶面设置为绝热壁面。其他边界设置为对称边界条件。一次侧与管壁、二次侧与管壁的网格连接方式采用1∶1连接方法,即数据直接传递。
3 结果分析及模型验证
3.1 模型验证
文献[5]中,为验证RPI数学模型的准确性,采用Bartolomei等[7]的实验结果进行对比。比较结果表明,本模型对过冷沸腾的模拟与实验结果符合较好,最大相对误差为3.2%。为验证网格独立性,分别对3套网格进行数值计算,网格数量分别为88万、111万和167万。结果显示,随着网格数量的增多,二次侧特征参数趋于定值。考虑到计算机性能等因素,本工作采用第2套网格。
3.2 传热管束内流动换热数值模拟
计算工况列于表1。管壁及一、二次侧工质的物性由查表可得。
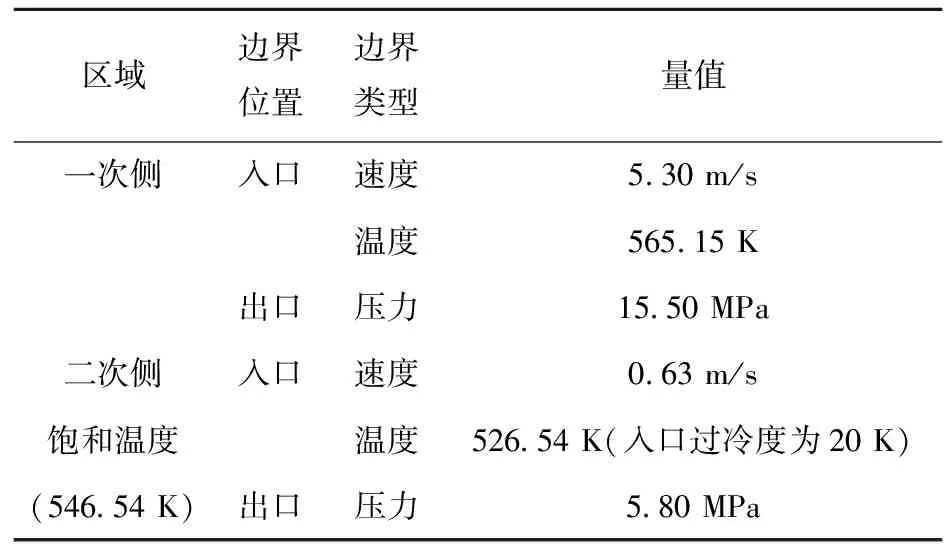
表1 计算工况
图3示出传热管束二次侧速度分布。由图3a明显看出,二次侧流体通过梅花孔支撑板时,由于流通截面的突缩,导致液相和气相速度迅速增大,其最大值分别为1.28 m/s和1.57 m/s。由于三叶梅花孔独特的结构,导致流体在流经梅花孔前后产生顺时针旋转流动,如图3b所示。同时还可看出,流体在孔板窄缝区的流速非常小。
传热管束流体及管壁温度分布示于图4。由图4a可见,一次侧高温流体从入口流入,将热量传递给二次侧,导致流体温度逐渐下降,而管壁温度却变化缓慢。由图4b可见,二次侧流体温度迅速上升,出口平均温度为543.11 K。同时,由于梅花孔支撑板的存在,梅花孔孔隙处的流体温度迅速上升,如图4b、c所示,此处空泡份额迅速增大,最终可能导致传热恶化,发生沸腾危机,因此应谨慎设计梅花孔支撑板。由图4c出口边界曲线上的温度分布可看出:由于梅花孔支撑板的存在,使得温度分布不再对称,对于管壁,左侧的温度要低于右侧的;而对于二次侧,则相反;对于一次侧,梅花孔支撑板的存在对于温度分布影响非常小。
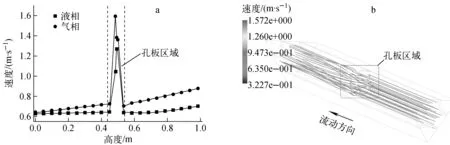
a——二次侧液相和气相速度;b——梅花孔支撑板局部速度
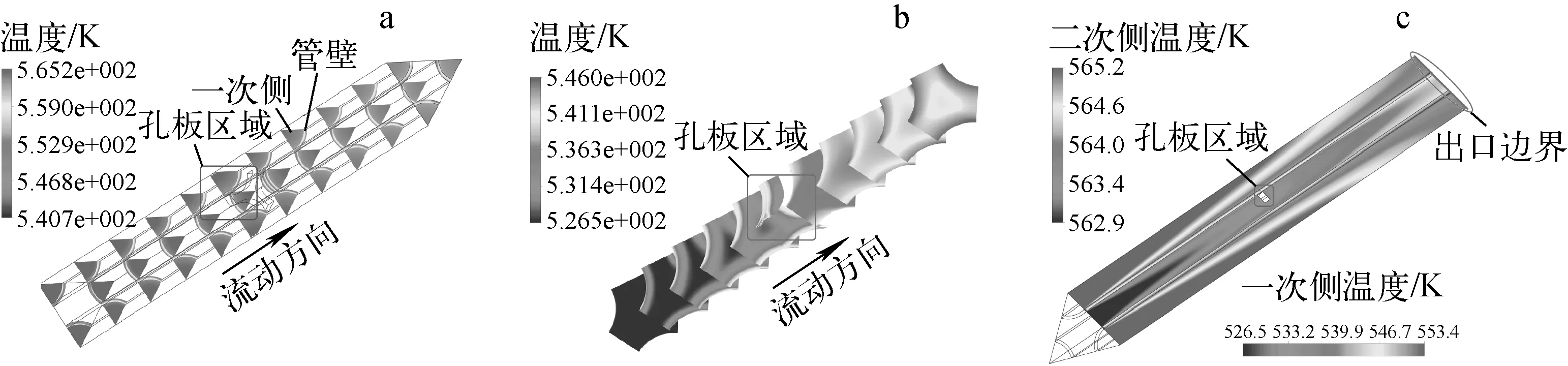
a——一次侧及管壁;b——二次侧;c——对称面处
图5示出传热管束二次侧空泡份额分布。由图5a可见,在离入口约0.17 m处发生过冷沸腾,流体在流经梅花孔支撑板处,空泡份额先下降,后上升,再下降,其最大值为0.024。随后,空泡份额迅速上升,在出口处达到0.091。由图5b可见,由于流体流经梅花孔所造成的旋转流动,导致空泡份额分布不均。但在梅花孔处,由于窄缝区域流速非常低,导致此处空泡份额迅速上升,达到最大值0.19。
从图5c可看出,梅花孔支撑板的存在使得空泡份额分布不再对称,线A上左侧的空泡份额要明显低于右侧的。
图6示出一、二次侧流体壁面平均换热系数随高度的变化。由图6a可见,一次侧换热系数随着高度的增加而增加,其平均换热系数为49 825 W/(m2·K),梅花孔支撑板的存在对一次侧换热系数造成的影响非常小。由图6b可见,二次侧换热系数变化较为复杂,换热系数先减小后缓慢增加,流经梅花孔支撑板处,传热系数突然上升,达到最大值27 058 W/(m2·K)。这主要是由于流通截面积的突缩使得此处对流换热大幅增强,导致沸腾加剧,从而增强了换热。二次侧平均换热系数为22 064 W/(m2·K)。
3.3 入口过冷度对传热管束热工水力特性的影响
本工作研究入口过冷度分别为30、25、20 K时对传热管束热工水力特性的影响,其他边界条件(表1)不变。
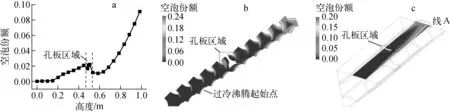
a——截面平均空泡份额;b——二次侧空泡份额;c——对称面空泡份额

a——一次侧;b——二次侧
不同入口过冷度下气、液相的速度特性曲线示于图7。由图7a可看出:入口过冷度对液相速度的影响很小,仅在出口处速度差异较大,随着入口过冷度的减小,液相速度增大。由图7b可看出:入口过冷度对气相速度的影响很大,这是由于热量的不断导入,使得壁面汽泡成核密度呈指数规律增加,产生出更多的汽泡;同时温度的升高也使汽泡密度变小,浮升力增大,最终导致汽泡速度增加。
图8示出不同过冷度下传热管束的温度特性曲线。由图8a可看出,随着入口过冷度的增加,一次侧入口与出口的温差逐渐增大,分别为1.68、1.84和2.02 K。梅花孔支撑板对一次侧温度分布的影响很小。由图8b可看出,二次侧温度随入口过冷度的降低而线性增加,梅花孔支撑板的存在使得孔板处的流体温度略微下降。由图8c可看出,当流体发生过冷沸腾时,不同入口过冷度下的管壁温度几乎为定值,分别为555.1、554.1和553.0 K。入口过冷度越小,管壁温度越大。在梅花孔支撑板处,管壁温度有一突降,且过冷度越低,温降越小。
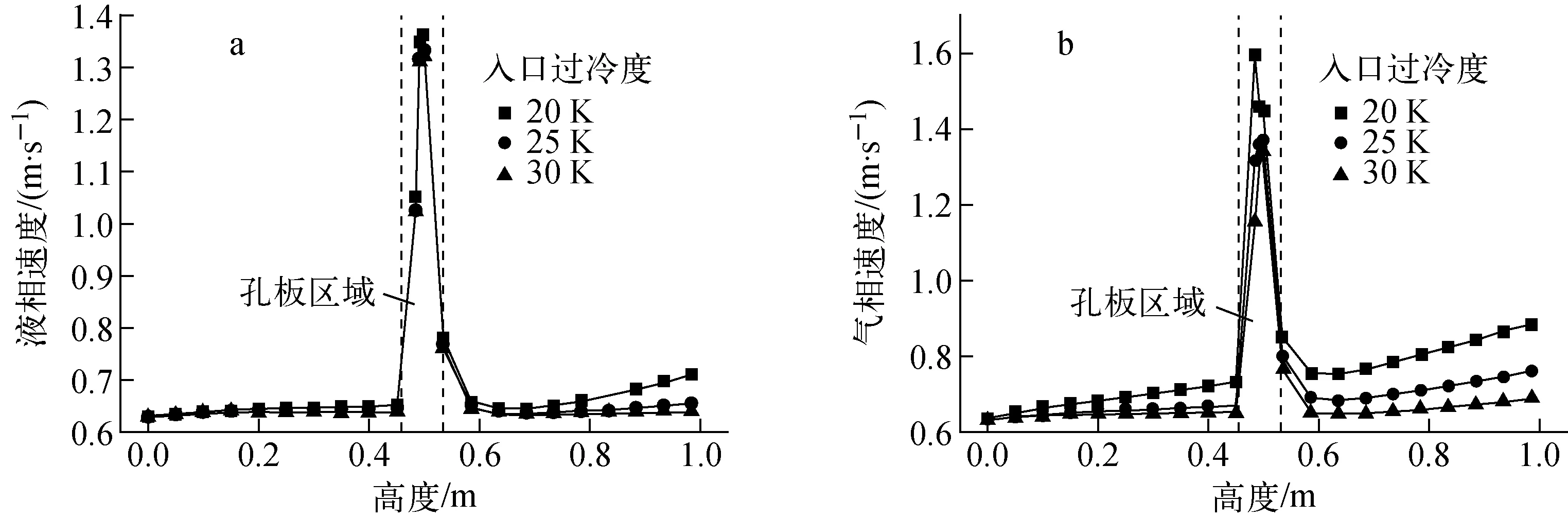
图7 不同入口过冷度下的速度特性曲线
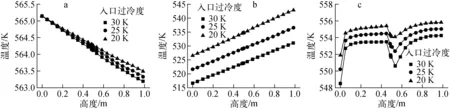
a——一次侧;b——二次侧;c——管壁
图9示出不同过冷度下的空泡份额分布。由图9可看出,随着过冷度的降低,空泡份额呈指数增加,这是由于过冷度的降低使得壁面温度增加(图8c),根据壁面汽泡成核密度方程,在饱和温度不变的情况下,壁面汽泡成核密度呈指数规律增加,最终导致空泡份额迅速增加。梅花孔处,由于热量的不断导入,过冷度越低,空泡份额越大。图10示出换热系数随入口过冷度的变化。由图10可见:对于一次侧,随着入口过冷度的增高,换热系数线性下降;对于二次侧,换热系数随着入口过冷度的增高而迅速下降。可见,出入口过冷度越低,传热管束换热特性越好。
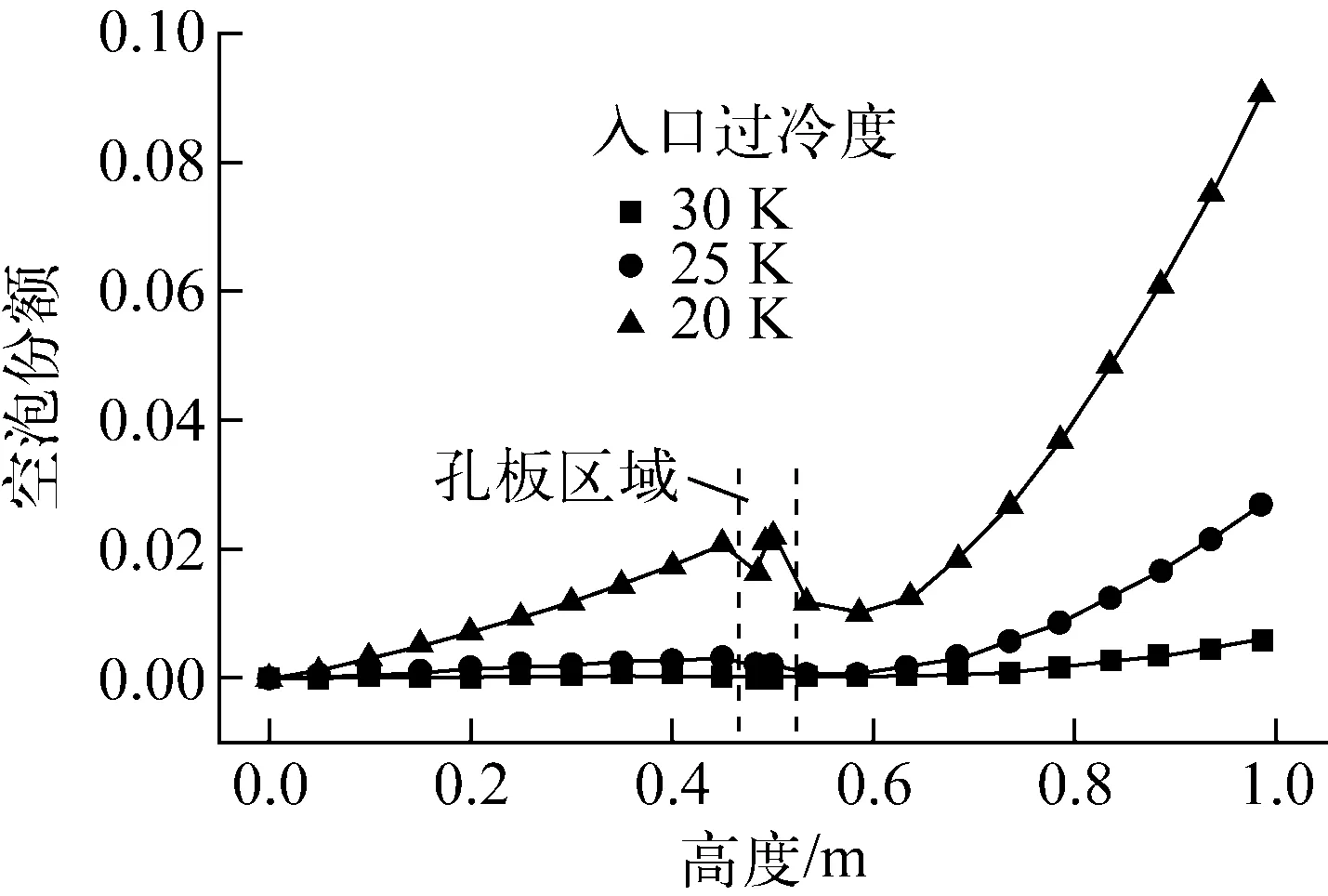
图9 不同过冷度下的空泡份额分布
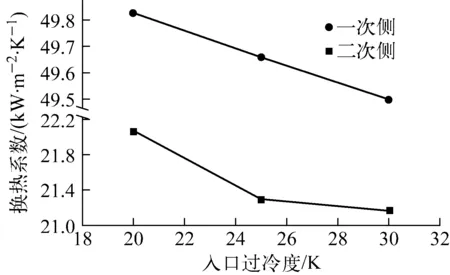
图10 换热系数随入口过冷度的变化
4 结论
本工作采用两流体欧拉数学模型并结合RPI壁面沸腾模型,对蒸汽发生器三角形排列且带三叶梅花孔支撑板结构的传热管束过冷沸腾区进行了数值分析,结论如下。
1) 精确模拟了一次侧、管壁及二次侧耦合传热过程,得到一、二次侧速度,温度,空泡份额分布及一、二侧换热系数。
2) 梅花孔支撑板的存在使得二次侧流体产生了顺时针的涡旋,导致二次侧温场、空泡份额分布不均。同时,梅花孔窄缝区存在空泡份额峰值,很容易导致此处传热恶化,管束损毁,因此需谨慎设计梅花孔支撑板。
3) 入口过冷度越低,气相与液相速度越大,传热管束温度变化越明显,空泡份额呈指数规律增加,换热性能越好。
参考文献:
[1] 戴玉龙,李志安,王翠花,等. 梅花形孔板支撑换热器壳程流场的数值分析[J]. 沈阳化工学院学报,2007,21(1): 25-28.
DAI Yulong, LI Zhi’an, WANG Cuihua, et al. Numerical analysis of flow field in shell of cinquefoil orifice baffle support type heat exchanger[J]. Journal of Shenyang Institute of Chemical Technology, 2007, 21(1): 25-28(in Chinese).
[2] HASSAN M, WEAVER D, DOKAINISH M. The effects of support geometry on the turbulence response of loosely supported heat exchanger tubes[J]. Journal of Fluids and Structures, 2003, 18(5): 529-554.
[3] SUN B, YANG Y. Numerically investigating the influence of tube support plates on thermal-hydraulic characteristics in a steam generator[J]. Applied Thermal Engineering, 2012, 51: 611-622.
[4] LI Yanjun, SUN Baozhi. Numerical investigation of thermal-hydraulic characteristics in a steam generator using a coupled primary and secondary side heat transfer model[J]. Annals of Nuclear Energy, 2013, 55(1): 258-264.
[5] 王成龙,从腾龙,王泽勇,等. 蒸汽发生器传热管一、二次侧耦合换热及管外过冷沸腾的数值研究[J]. 原子能科学技术,2014,48(4):610-616.
WANG Chenglong, CONG Tenglong, WANG Zeyong, et al. Numerical investigation of coupled heat transfer between primary and secondary side of SG tube and subcooled flow boiling on secondary side[J]. Atomic Energy Science and Technology, 2014, 48(4): 610-616(in Chinese).
[6] KURUL N, PODOWSKI M. On the modeling of multidimensional effects in boiling channels[C]∥Proceedings of the 27th National Heat Transfer Conference. [S. l.]: [s. n.], 1991.
[7] BARTOLOMEI G G, BRANTOV V G, MOLOCHNIKOV Y S, et al. An experimental investigation of true volumetric vapour content with subcooled boiling in tubes[J]. Thermal Engineering, 1982, 29(3): 132-135.

