一道2013年甘肃省预赛试题的解法、源头及推广

●

(会宫中学 安徽枞阳 246740)

1 试题及解法

图1

(2013年甘肃省数学竞赛预赛试题第9题)

从而

由梯形的中位线定理及抛物线的定义,可得

从而

解法2由抛物线定义得

|AF|+|BF|= |AA1|+|BB1|=2|MN|,

故

又在△ABF中,

|AB|2= |AF|2+|BF|2-2|AF|·|BF|cos120°,

即

|AB|2=(|AF|+|BF|)2-|AF|·|BF|.

又

则

即

因此

当且仅当|AF|=|BF|时,取到等号.

2 题源探究

我们发现,这道试题是由2012年全国高中数学联赛的一道试题改编而来的.

(2012年全国高中数学联赛试题第4题)

按照例1的2种解法可求得最大值为1.

3 试题推广

证明设∠ABF=θ(其中0<θ<π-α),则由正弦定理得

从而

由梯形的中位线定理及抛物线的定义,得

从而

由此得到定理1.

4 类比研究

在椭圆和双曲线中也有类似的结论.

图2

证明如图2,设点A,B在l上的投影分别为A1,B1,则

由梯形的中位线定理,得

在△ABF中,设∠ABF=θ(其中0<θ<π-α),则由正弦定理得

从而

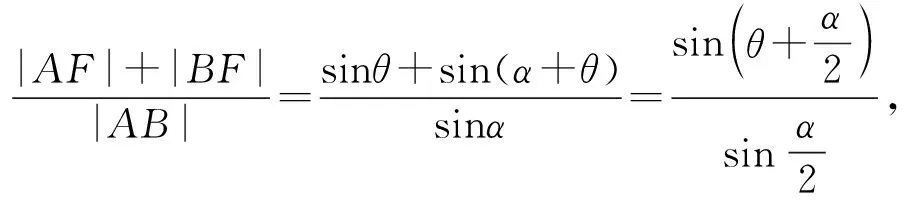
因此

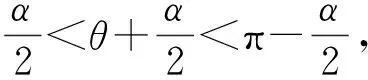
因此

当点F为左焦点、l为左准线时,也有相应的结论.

易知抛物线的离心率为1,将e=1代入定理2和定理3即为定理1，因此以上3个定理可以统一为如下定理: